Тема 2. Модель множественной регрессии

1. . Методические указания

Множественная регрессия — уравнение связи с несколькими независимыми переменными:

,

где у — зависимая переменная (результативный фактор); 

,  — независимые, или объясняющие, переменные (факторы).

Наиболее распространенной в эконометрике является линейная модель множественной регрессии:

,

где  — параметры уравнения регрессии;

 — случайная ошибка.

По выборке ограниченного объема оценивается выборочное уравнение регрессии:

(1)

где — оценки параметров соответственно.

Данные выборки можно представить в матричной форме:

 — вектор значений зависимой переменной размерности ;

 — значение переменной в наблюдении , ;

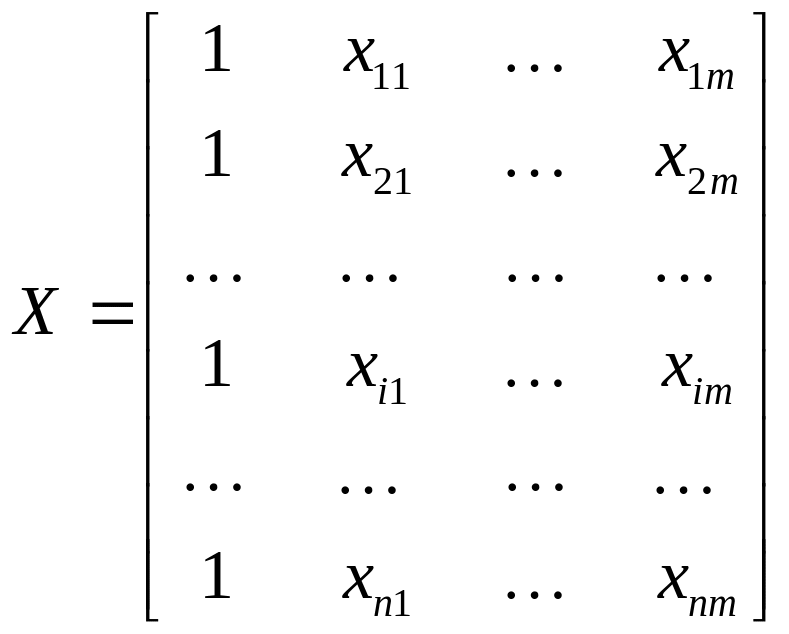
матрица значений независимых переменных размерности ,  — значения переменных в наблюдении . Первый столбец этой матрицы является единичным, так как в уравнении (1) присутствует свободный член;

 — 

вектор оценок параметров модели размерности .

 — 

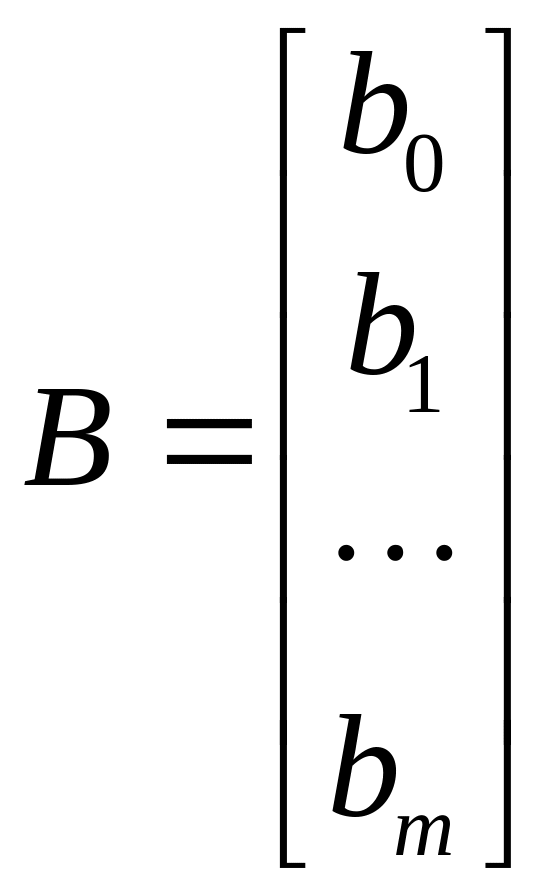
Для оценки параметров модели применяется метод наименьших квадратов (МНК). Для линейных и нелинейных уравнений, приводимых к линейным, получают систему из линейного уравнения с неизвестными. Количество уравнений равняется количеству неизвестных переменных, поэтому решение системы можно найти, например, с помощью метода Крамера.

Для двухфакторной модели данная система будет иметь вид:

(2)

Формулы Крамера:

(3)

где — определитель системы;

— частные определители, которые получают путем замены соответствующего столбца матрицы определителя системы столбцом свободных членов.

Решением системы нормальных уравнений в матричной форме будет вектор оценок:

. (4)

По уравнению регрессии могут быть найдены средние коэффициенты эластичности

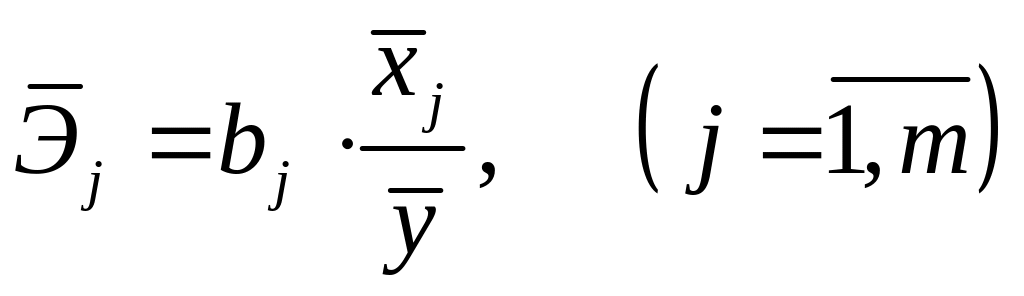, (5)

которые показывают, на сколько процентов в среднем изменится результат при изменении соответствующего фактора на 1% при фиксированном значении других факторов.

Адекватность построенной модели в целом оценивает коэффициент множественной детерминации R², который измеряет долю дисперсии, совместно объясненной независимыми переменными, и определяется по формуле

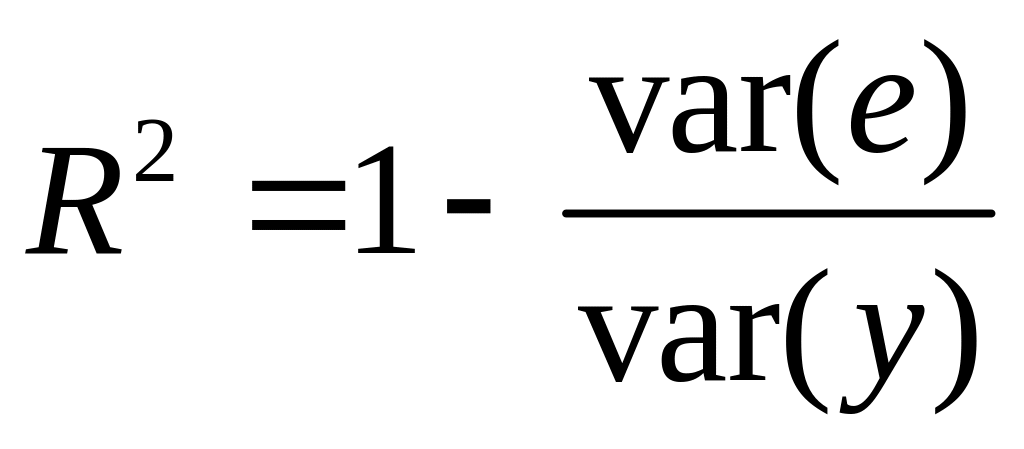, (6)

где 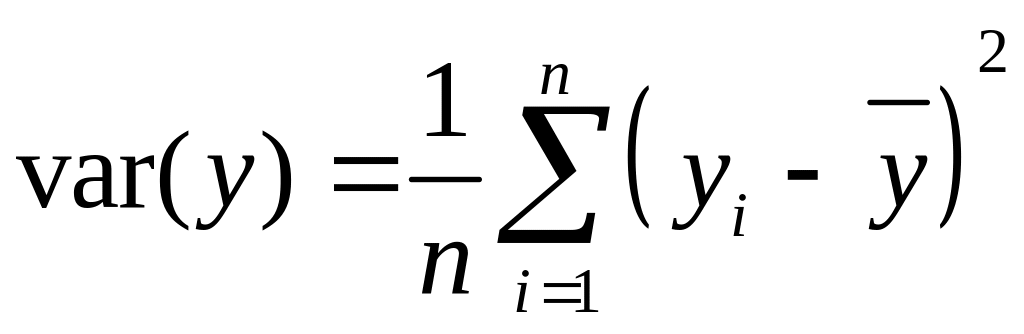— общая дисперсия результативного фактора;

var (e) = — остаточная дисперсия.

Скорректированный коэффициент множественной детерминации содержит поправку на число степеней свободы и дает такую оценку тесноты связи, которая не зависит от числа факторов в модели. Он рассчитывается по формулам (7) или (8)

(7)

(8)

где m — число независимых факторов;

n — число наблюдений.

Чем больше величина m, тем сильнее различия и .

Оценивание качества уравнения регрессии в целом состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии. Для этого выполняется сравнение фактического F_факт и критического F_крит значений критерия Фишера. F_факт рассчитывается по формуле

, (9)

где m — число параметров при переменных х (в линейной регрессии совпадает с числом включенных в модель факторов); n — число наблюдений.

Вычисленный критерий F_факт сравнивается с критическим значением F_крит, найденным по двум степеням свободы: ν₁ = m, ν₂ = n – m – 1, уровню значимости .

Если F_факт < F_крит, то гипотеза Н₀ принимается и признается статистическая незначимость, ненадежность уравнения регрессии.

Если F_факт > F_крит, то гипотеза Н₀ о случайной природе оцениваемых характеристик отвергается, признается статистическая значимость уравнения, оно может быть использовано для объяснения изменения переменной y под влиянием изменения переменной x.

Квадратный корень из коэффициента множественной детерминации называется коэффициентом множественной корреляции.

Границы изменения коэффициента множественной корреляции – от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.

Несмещенной оценкой дисперсии случайной ошибки является величина (остаточная дисперсия на одну степень свободы):

. (10)

Величина называется стандартной ошибкой регрессии.

Для расчета стандартных ошибок коэффициентов регрессии применяются формулы:

, (11)

где индексом обозначен элемент матрицы , стоящий на главной диагонали (нумерацию строк начинают с 0). Значимость коэффициента регрессии оценивается с помощью -критерия Стьюдента:

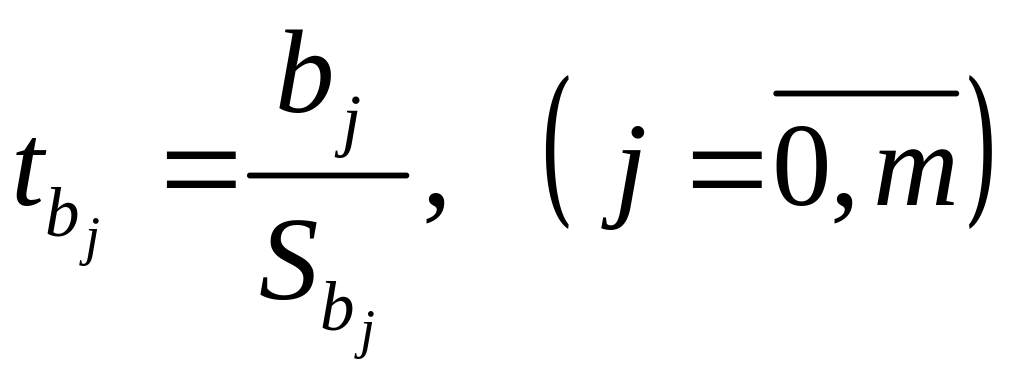. (12)

Найденные значения затем сравниваются с табличными значениями при заданном уровне значимости и числе степеней свободы . Если , то коэффициент признаётся незначимым, если , то коэффициент регрессии является статистически значимым, надежным.

При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:

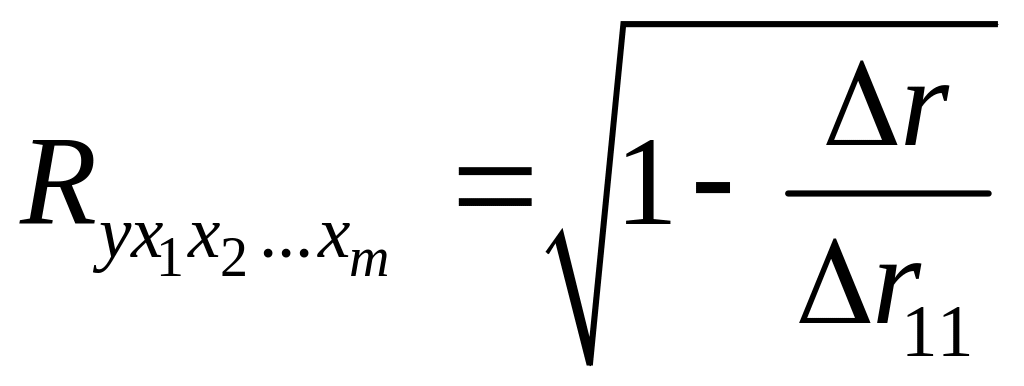, (13)

где

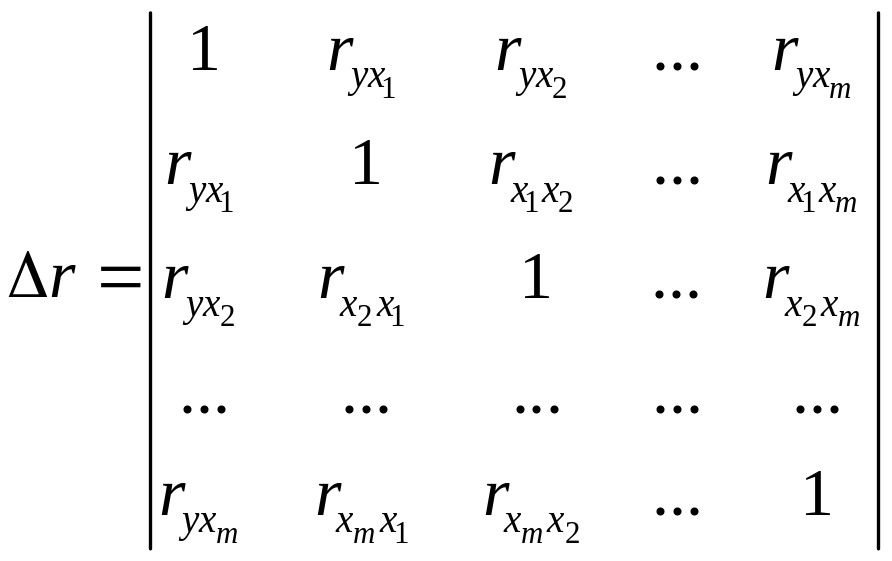(14)

— определитель матрицы парных коэффициентов корреляции;

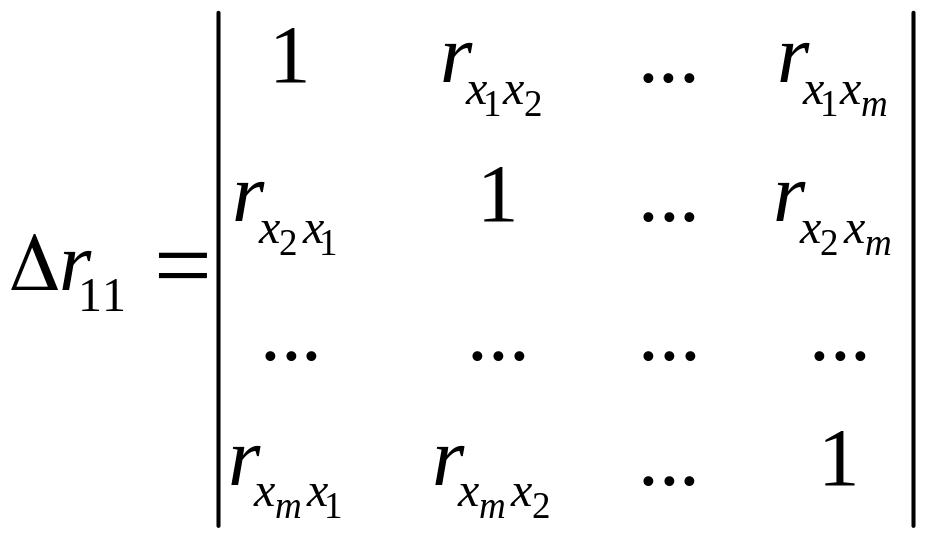(15)

— определитель матрицы межфакторной корреляции. В случае двух факторов формулы (14) и (15) примут вид:

; (16)

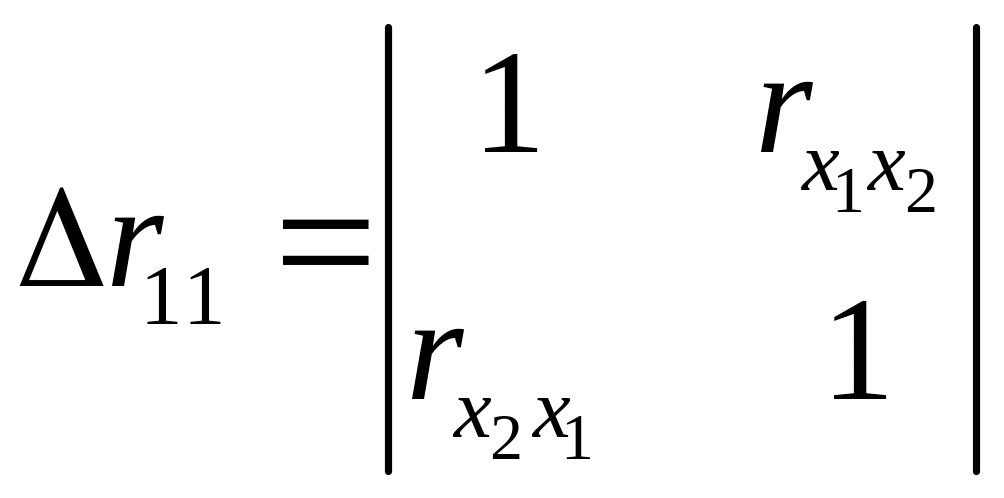. (17)

При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов. Для оценки ее наличия может использоваться определитель матрицы коэффициентов межфакторной корреляции (15). Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Ранжирование факторов, участвующих во множественной линейной регрессии, может быть достигнуто с помощью частных коэффициентов корреляции (для линейных связей), которые характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.

При двух факторах формулы для расчета частных коэффициентов корреляции примут вид:

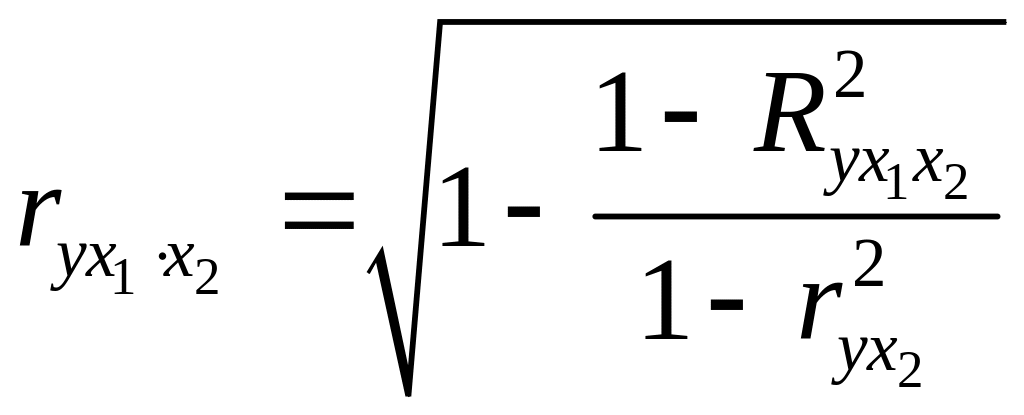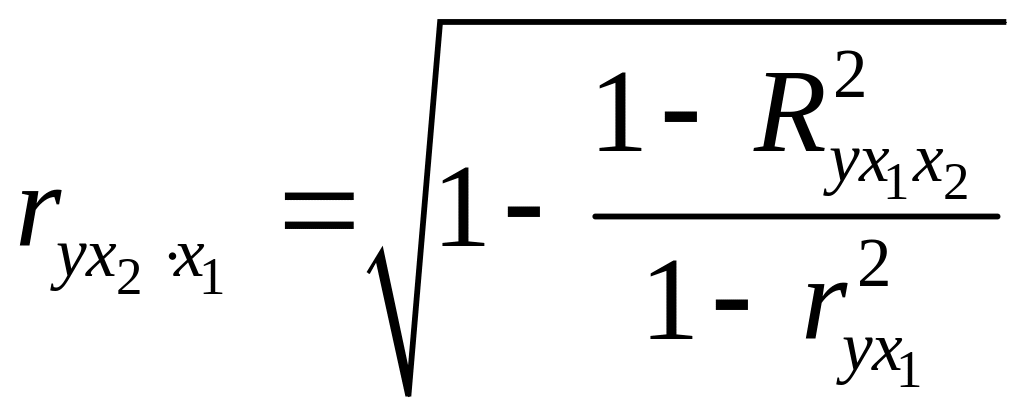; . (18)

Мерой для оценки включения фактора в модель служит частный -критерий, т.е. .

Фактическое значение частного F-критерия сравнивается с критическим при уровне значимости  и числе степеней свободы: ν₁ = 1 и ν₂ = = n – m – 1. Если фактическое значение превышает , то дополнительное включение фактора в модель статистически оправдано и коэффициент чистой регрессии при факторе статистически значим. Если же фактическое значение меньше табличного, то дополнительное включение в модель фактора не увеличивает существенно долю объясненной дисперсии признака у, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.

Для двухфакторного уравнения частные F-критерии имеют вид:

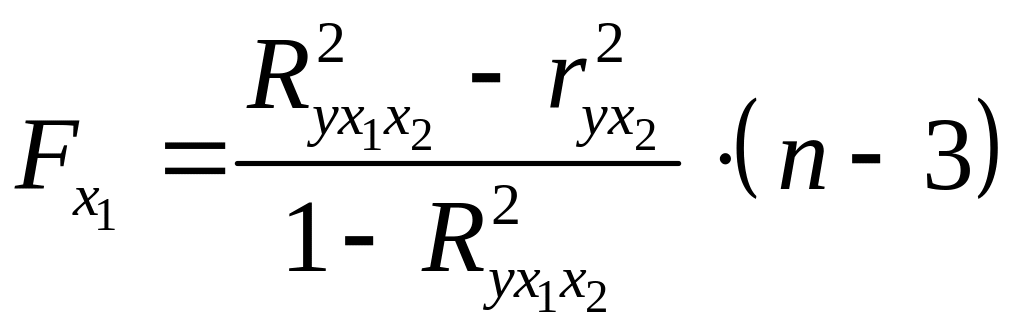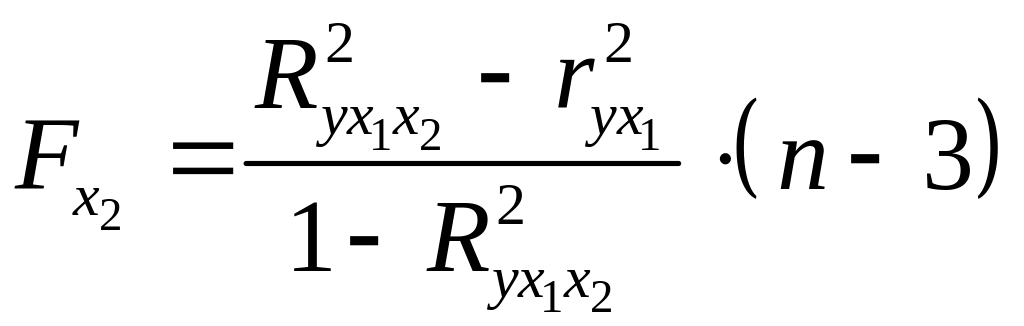, . (19)

С помощью частного F-критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор вводился в уравнение множественной регрессии последним.