2. Практическое задание

По регионам исследуется зависимость среднедневной заработной платы (фактор ) от прожиточного минимума (фактор ). Данные по вариантам приведены в папке Эконометрика \ Задание 1.

Требуется:

1. По данным варианта построить поле корреляции и сформулировать гипотезу о форме связи между факторами и .

2. Рассчитать оценки параметров уравнения линейной регрессии для факторов и . Проверить полученный результат с использованием функции ЛИНЕЙН.

3. Оценить силу линейной зависимости между факторами с помощью линейного коэффициента парной корреляции.

4. Проверить качество построенной модели с помощью средней ошибки аппроксимации и коэффициента детерминации. Проверить значимость коэффициента детерминации с помощью 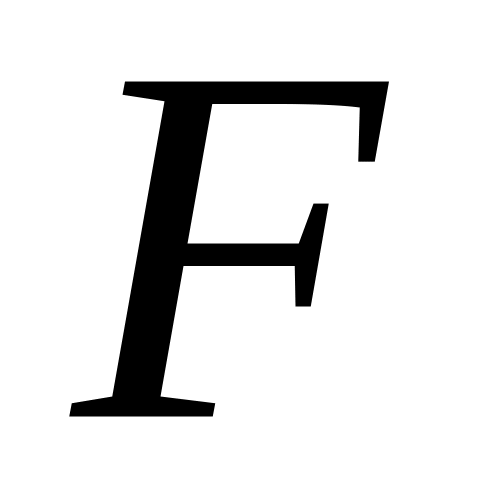-критерия Фишера при уровне значимости α = 0,01. Сделать выводы.

5. Оценить статистическую значимость коэффициентов регрессии с помощью -критерия Стьюдента, принимая уровень значимости α = 0,01. Сделать вывод. Найти границы доверительных интервалов коэффициентов.

6. На поле корреляции построить эмпирическую линию регрессии, вывести уравнение и значение коэффициента детерминации. Сравнить вычисленный в пункте 4 коэффициент детерминации с приведенным на корреляционном поле.

7. Построить графики степенной, экспоненциальной, логарифмической парных регрессий на и вывести уравнения этих регрессий и коэффициенты детерминации.

8. Рассчитать средние ошибки аппроксимации для степенного, экспоненциального и логарифмического уравнений регрессии.

9. Построить сводную таблицу, записав в нее найденные уравнения регрессии, коэффициенты детерминации и средние ошибки аппроксимации. Выбрать уравнение, наилучшим образом соответствующее данным наблюдений, и обосновать выбор.

10. По выбранному уравнению рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 30% от максимального уровня. Оценить точность прогноза, рассчитав стандартную ошибку предсказания и доверительный интервал для прогнозного значения результата.

Указание

Используя Проводник, следует создать на диске, указанном преподавателем, папку с именем ФИО / Эконометрика. Далее нужно скопировать в созданную папку рабочую книгу в соответствии с вариантом из папки Эконометрика \ Задание 1 и выполнять решение задания.

3. Решение типового задания

Пример. По территориям региона приводятся данные за 200X г. (табл. 1).

Таблица 1

Номер региона	Прожиточный минимум, ден. ед. (х)	Среднедневная заработная плата, ден. ед. (у)
1	78	133
2	82	148
3	87	134
4	79	154
5	89	162
6	106	195
7	67	139
8	88	158
9	73	152
10	87	162
11	76	159
12	115	173

Требуется:

1. Построить поле корреляции и сформулировать гипотезу о форме связи между факторами х и у.

2. Рассчитать оценки параметров уравнения линейной регрессии. Проверить результат с использованием функции ЛИНЕЙН.

3. Рассчитать линейный коэффициент парной корреляции. Оценить силу линейной зависимости между факторами.

4. Рассчитать среднюю ошибку аппроксимации. Сделать вывод.

5. Рассчитать коэффициент детерминации, проверить его значимость с помощью F - критерия Фишера при уровне значимости  = 0,05. Сделать вывод.

6. Оценить статистическую значимость коэффициентов регрессии с помощью t - критерия Стьюдента, принимая уровень значимости  = 0,05. Сделать вывод. Найти границы доверительных интервалов коэффициентов.

7. На поле корреляции построить эмпирическую прямую, вывести её уравнение и коэффициент детерминации 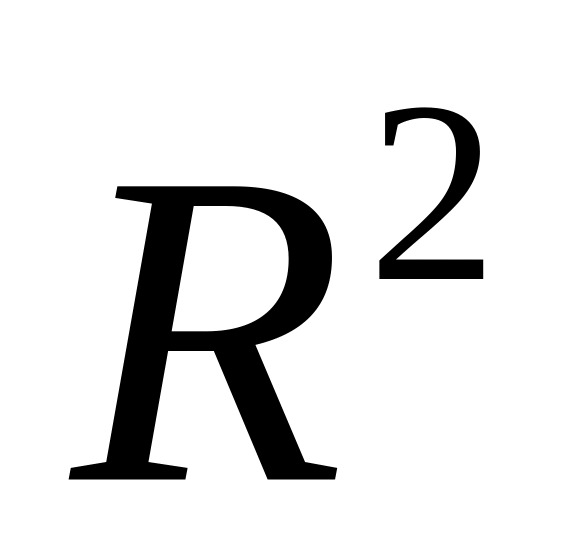с использованием опции Линия тренда. Сравнить , вычисленный в пункте 5, с приведенным на диаграмме.

8. Построить графики степенной, экспоненциальной, логарифмической парной регрессии у от х и вывести уравнения этих регрессий и коэффициенты детерминации с использованием опции Линия тренда.

9. Рассчитать средние ошибки аппроксимации для степенного, экспоненциального и логарифмического уравнений регрессии.

10. Построить сводную таблицу, записав в нее найденные уравнения регрессии, коэффициенты детерминации и средние ошибки аппроксимации. Выбрать уравнение, наилучшим образом соответствующее данным наблюдений, и обосновать выбор.

11. По выбранному уравнению рассчитать прогнозное значение результата, если прогнозное значение фактора X увеличится на 10% от максимального уровня. Оценить точность прогноза, рассчитав стандартную ошибку предсказания и доверительный интервал для прогнозного значения результата.