КОМПЬЮТЕРНЫЙ ПРАКТИКУМ ПО ЭКОНОМЕТРИКЕ

(выполнение расчетов в среде Excel)

Учебно-методическое пособие

СОДЕРЖАНИЕ

Введение 4

Тема 1. Модель парной регрессии 5

1.1. Методические указания 5

1.2. Практическое задание 9

1.3. Решение типового задания 10

Тема 2. Модель множественной регрессии 24

2.1. Методические указания 24

2.2. Практическое задание 29

2.3. Решение типового задания 30

Литература 43

Введение

«Компьютерный практикум по эконометрике (выполнение расчетов в среде Excel)» подготовлен в соответствии с учебной программой по дисциплине «Эконометрика» с учетом требований к подготовке студентов по экономическим специальностям: «Бухгалтерский учет, анализ и аудит», «Финансы и кредит», «Менеджмент», «Экономика и управление на предприятии», «Мировая экономика и международные экономические отношения».

При выборе программного средства для проведения практикума авторы руководствовались тем, что MS Excel – один из наиболее популярных пакетов в среде Windows. Этот пакет обеспечивает разнообразные методы обработки статистических данных, в частности, позволяет выполнять парный и множественный регрессионный анализ.

П особие включает две темы. Каждая из них содержит необходимый объем теоретического материала, практическое задание, варианты для выполнения задания, разобранные примеры выполнения задания.

Пособие предназначено для студентов, которые прослушали базовые курсы по высшей математике, теории вероятностей и математической статистике, информационным технологиям в экономике и имеют навыки работы в среде MS Excel.

Тема 1. Модель парной регрессии

1. Методические указания

Парная регрессия — уравнение связи между двумя переменными — и

y = ,

где — зависимая переменная (результативный фактор); — независимая, или объясняющая, переменная (фактор).

Различают линейные и нелинейные уравнения регрессии.

Линейное уравнение регрессии: ,

где и — параметры уравнения регрессии, — случайная величина, характеризующая отклонение от уравнения регрессии и включающая влияние неучтенных в модели факторов, случайных ошибок и особенностей измерения.

Нелинейные регрессии делятся на два класса:

1. регрессии, нелинейные по объясняющим переменным:

• многочлены различных степеней ;

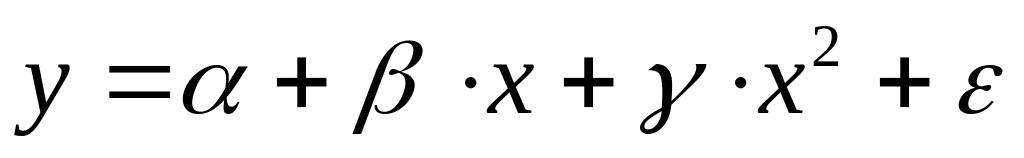• дробно-линейная регрессия ;

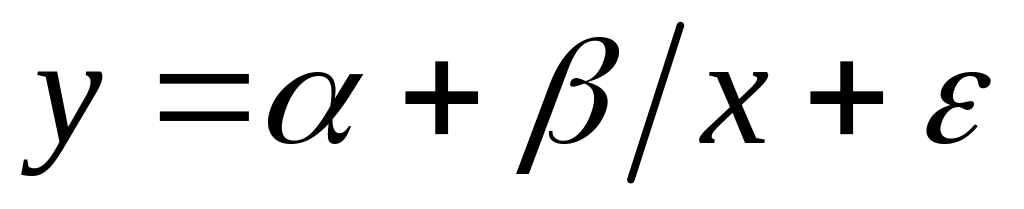2. регрессии, нелинейные по оцениваемым параметрам:

   • степенная регрессия ;

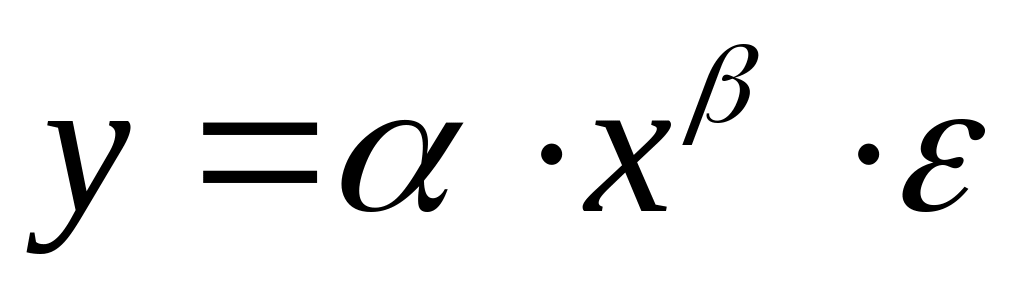   • показательная регрессия ;

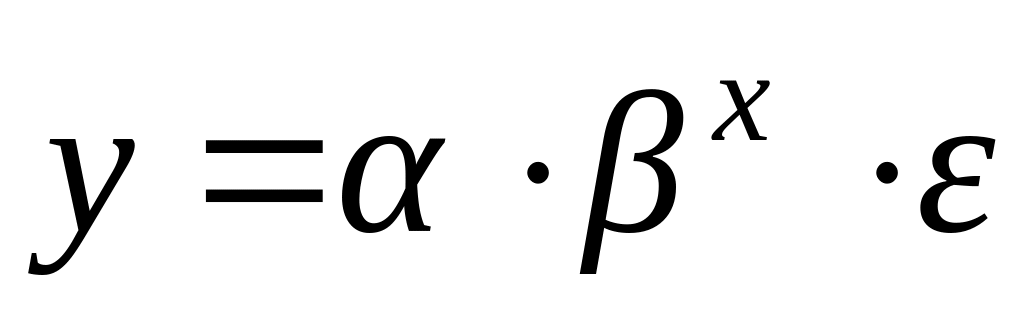   • экспоненциальная регрессия .

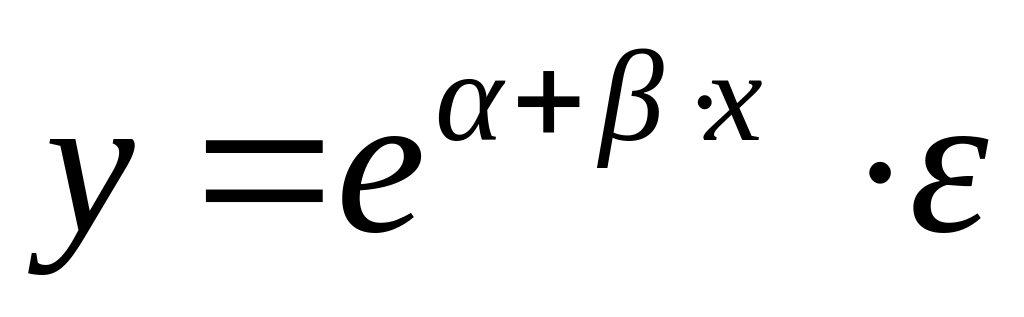Выбор вида уравнения регрессии может быть осуществлен, например, графическим методом, который основан на построении диаграммы рассеяния (поля корреляции). Для получения диаграммы в прямоугольной системе координат отмечают точки , , где n — количество наблюдаемых пар значений переменных и .

Нахождение уравнения регрессии сводится к оценке его параметров. По выборке ограниченного объема можно построить так называемое эмпирическое уравнение регрессии:

= a + b x, (1)

где a и b — коэффициенты уравнения являются оценками параметров и соответственно.

Для определения коэффициентов моделей применяется метод наименьших квадратов (МНК). Для линейных и нелинейных уравнений, приводимых к линейным, получают систему уравнений относительно коэффициентов и :

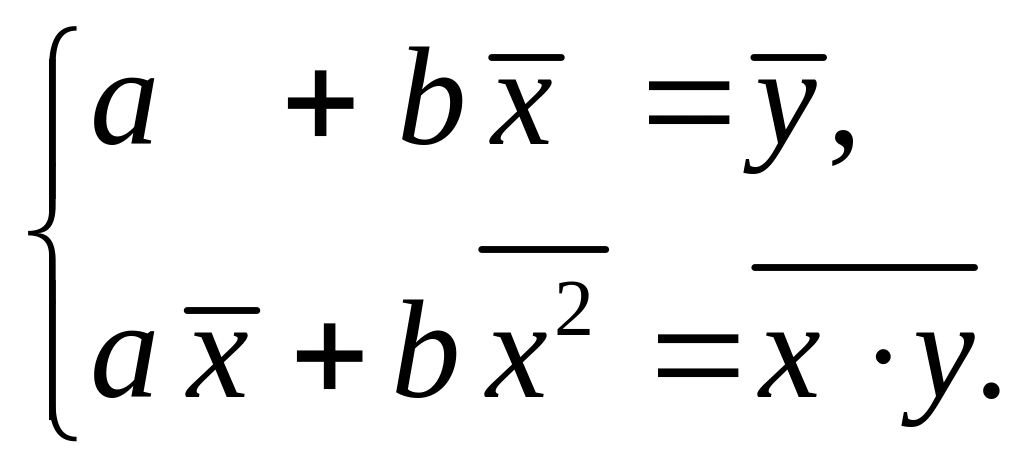(2)

Для вычисления и можно воспользоваться готовыми формулами, которые следуют непосредственно из решения системы, например по методу Крамера:

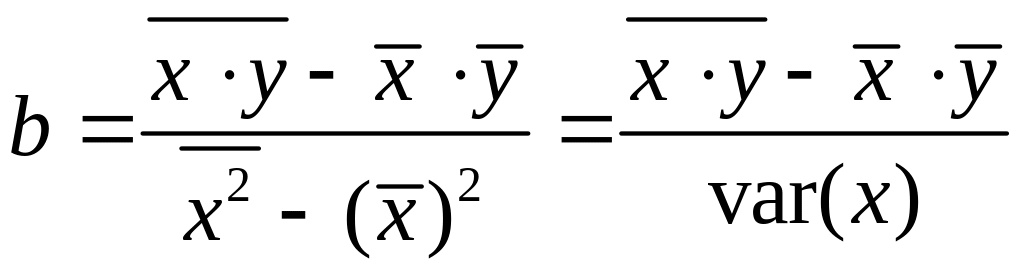, (3)

, (4)

где , , , , — средние значения:

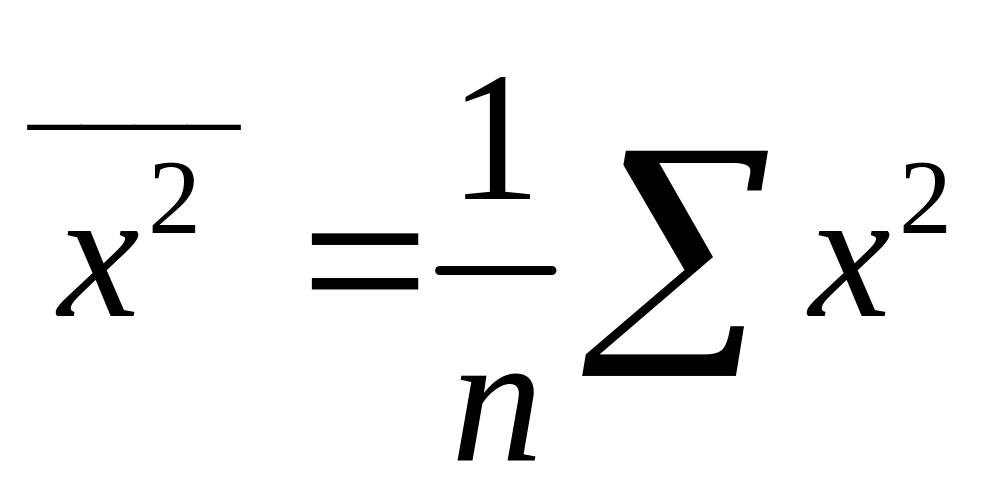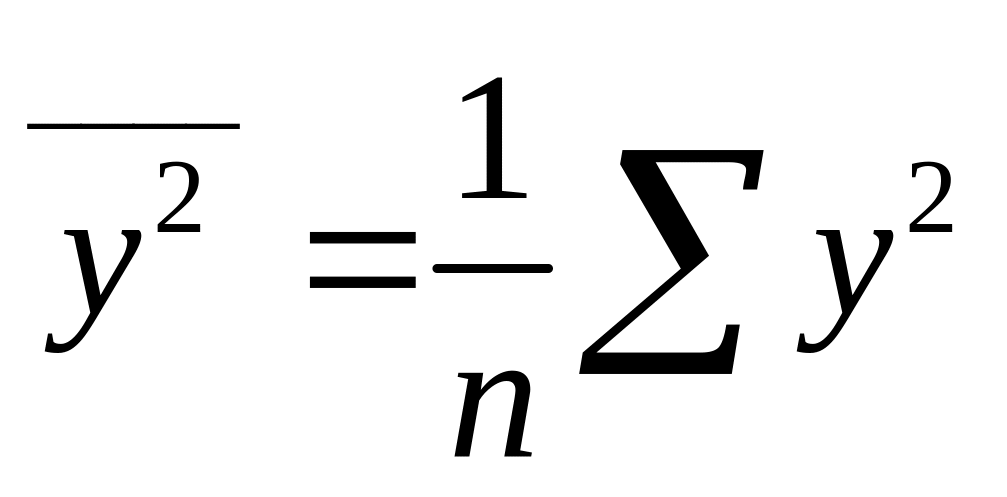; ; ; ; , (5)

— дисперсия независимого фактора , которая может быть вычислена по формуле

. (6)

В расчетах используют , дисперсию результативного фактора , которую вычисляют аналогично

. (7)

Показателем тесноты связи при использовании линейной регрессии является линейный коэффициент парной корреляции ( ):

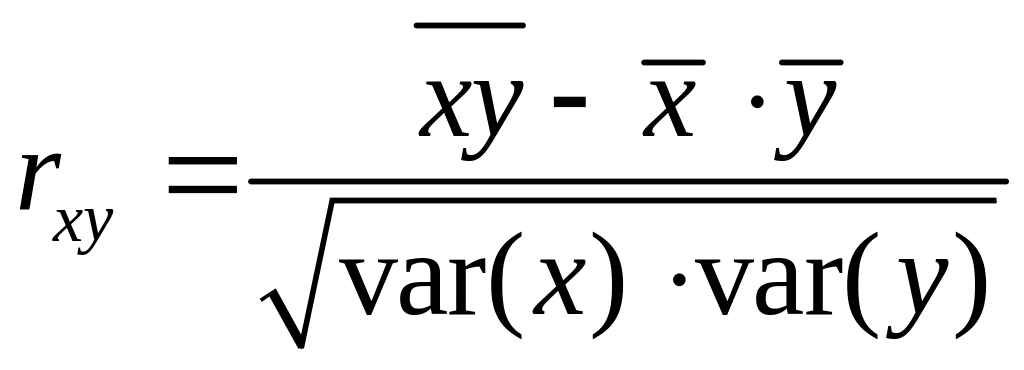. (8)

При нелинейной регрессии находят индекс корреляции (0 ≤ ρ_xy ≤ 1):

= , (9)

где — общая дисперсия результативного фактора , определяемая как

var (y) = , (10)

(формула (7) для вычисления является упрощением формулы (10));

var ( )  — дисперсия расчетных значений :

var ( ) = , (11)

 — дисперсия остатков:

var (e) = . (12)

О качестве построенной модели регрессии можно судить:

1) по средней ошибке аппроксимации

. (13)

Допустимый предел значений — не более 8 – 10%;

2) по коэффициенту детерминации R² (0 ≤ R² ≤ 1):

R² = . (14)

Чем лучше уравнение регрессии соответствует наблюдениям, тем меньше var(e) и тем ближе R² к единице, и наоборот, чем «хуже» подгонка линии регрессии к данным, тем ближе значение R² к нулю.

Оценивание качества уравнения регрессии в целом состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии. Для этого выполняется сравнение наблюдаемого (эмпирического, фактического) и критического (табличного) F_крит значений критерия Фишера.

рассчитывается по формуле

. (15)

Вычисленное значение сравнивается с критическим значением F_крит, найденным по таблицам распределения Фишера по двум степеням свободы: ν₁ = 1, ν₂ = n – 2, уровню значимости .

Если F_факт < F_крит, то гипотеза Н₀ принимается и признается статистическая незначимость, ненадежность уравнения регрессии.

Если F_факт ≥ F_крит, то гипотеза Н₀ отвергается, признается статистическая значимость уравнения. Полученная модель может быть использована для объяснения изменения переменной y под влиянием изменения переменной x.

Для оценки статистической значимости коэффициентов регрессии выдвигается гипотеза Н₀ о случайной природе показателей, т.е. о незначимом их отличии от нуля. Для оценки существенности каждого из коэффициентов а и b его величина сравнивается с его стандартной ошибкой, т.е. определяются фактические значения – критерия Стьюдента:

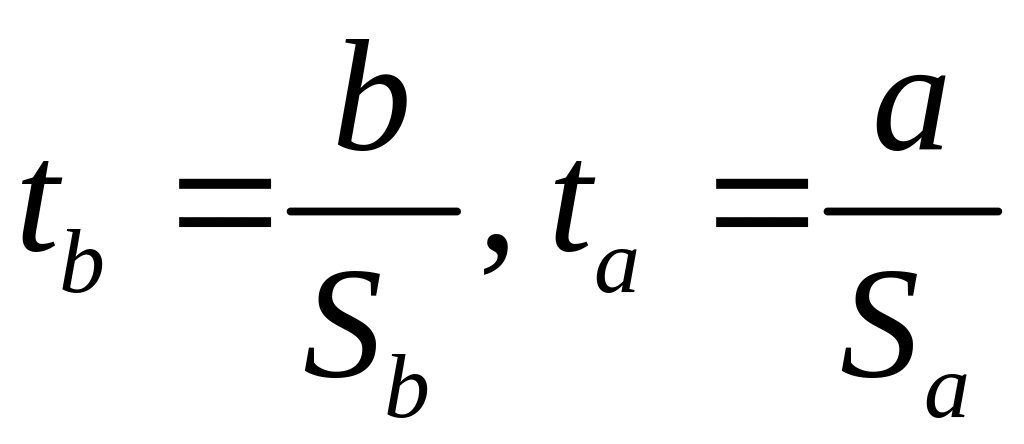, (16)

которые затем сравниваются с табличным значением при заданном уровне значимости и числе степеней свободы .

Стандартные ошибки коэффициентов регрессии определяются по формулам:

= ; (17)

= , (18)

где = ·var(e) = — остаточная дисперсия регрессии.

Если , то Н₀ принимается и признаётся случайная природа формирования коэффициентов (а, b); если , то Н₀ отвергается, т.е. коэффициенты (а, b) не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора .

Доверительные интервалы для параметров регрессии определяются с помощью неравенств:

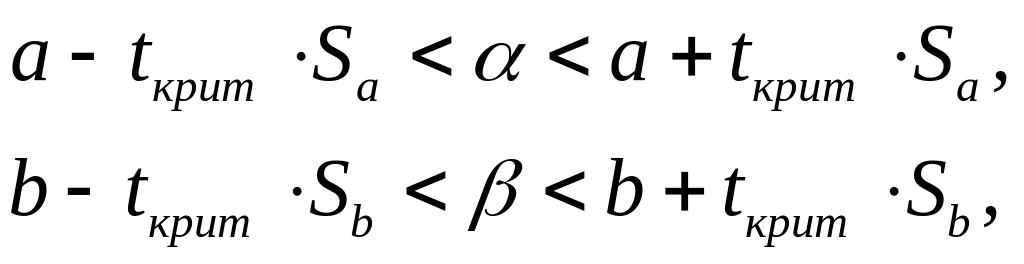
(19)

и с надежностью покрывают определяемые параметры α и β.

Если нижняя граница интервала отрицательна, а верхняя – положительна, то оцениваемый параметр полагается равным нулю.

Прогнозное значение вычисляется при подстановке в эмпирическое уравнение регрессии соответствующего (прогнозного) значения :

= a + b x_р. (20)

Стандартная ошибка предсказания может быть рассчитана по формуле

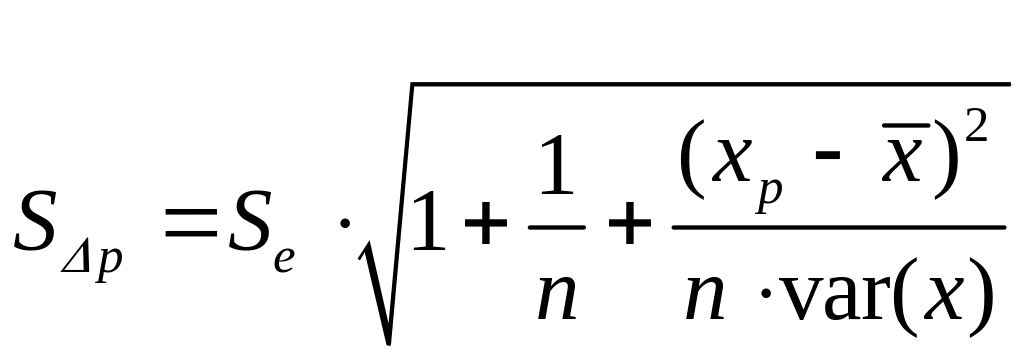, (21)

где S_e = — стандартная ошибка регрессии.

Доверительный интервал для действительного значения y_р зависимой переменной определяется выражением

– t_крит∙ S_Δp < y_р < + t_крит∙ S_Δp,. (22)

Средний коэффициент эластичности показывает, на сколько процентов отклонится в среднем результат от своей средней величины, если фактор изменится на 1% от своего среднего значения:

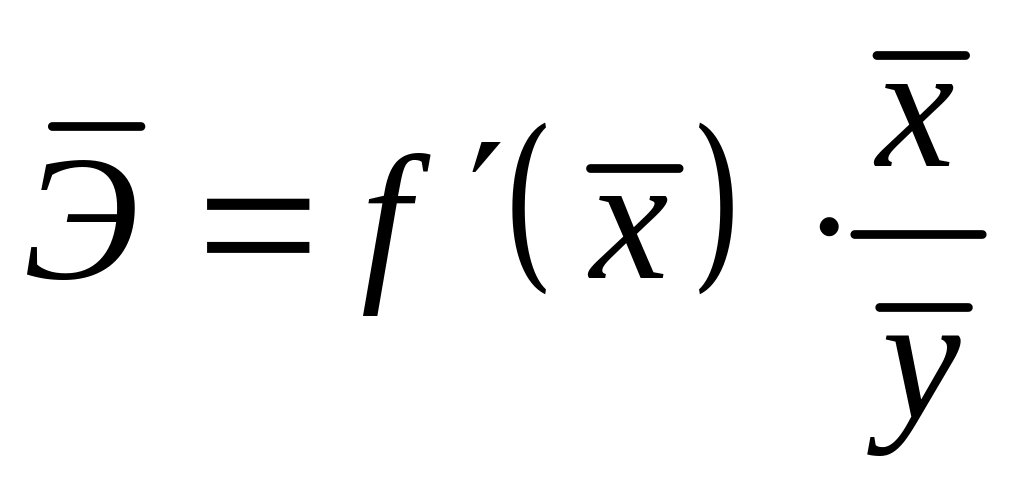. (23)