
- •Года: 97/98, 98/99, 99/00, 00/01, 01/02, 02/03, 03/04.
- •1997/1998 Учебный год. Вариант 1.
- •1997/1998 Учебный год. Вариант 2.
- •1999/2000 Учебный год. Вариант 2.
- •1999/2000 Учебный год. Вариант 3.
- •1999/2000 Учебный год. Вариант 4.
- •1999/2000 Учебный год. Вариант 5.
- •1999/2000 Учебный год. Вариант 6.
- •2000/2001 Учебный год. Вариант 1.
- •2000/2001 Учебный год. Вариант 2.
- •2000/2001 Учебный год. Вариант 3.
- •2000/2001 Учебный год. Вариант 4.
- •2000/2001 Учебный год. Вариант 5.
- •2001/2002 Учебный год. Вариант 1.
- •2001/2002 Учебный год. Вариант 2.
- •2001/2002 Учебный год. Вариант 3.
- •2001/2002 Учебный год. Вариант 4.
- •2001/2002 Учебный год. Вариант 5.
- •2002/2003 Учебный год. Вариант 1.
- •2002/2003 Учебный год. Вариант 2.
- •2002/2003 Учебный год. Вариант 3.
2000/2001 Учебный год. Вариант 5.
Задача
11.
Привести
квадратичную форму
 к каноническому виду и указать линейное
отображение, осуществляющее это
преобразование.
к каноническому виду и указать линейное
отображение, осуществляющее это
преобразование.
Ответ. Канонический вид квадратичной формы: .
Отображение осуществляется по формулам:
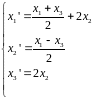
Задача 12. Совпадает с задачей 12 из варианта 4.
2001/2002 Учебный год. Вариант 1.
Задача 1. Найти комплексные корни многочлена

Решение.
Заметим, что 2 корня этого многочлена
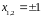 .
Поделим многочлен
.
Поделим многочлен
 на многочлен
на многочлен
 .
Получаем:
.
Получаем:
 .
Оставшиеся корни находим по формуле
корней квадратного трехчлена
.
Оставшиеся корни находим по формуле
корней квадратного трехчлена
 .
.
Задача
2.
Найти матрицу
 и исследовать ее зависимость от параметра
и исследовать ее зависимость от параметра
 .
.

Решение. Находим обратную матрицу.

При
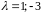 определитель матрицы
нулевой и матрица
не имеет обратной. При остальных же
значениях параметра
получается
определитель матрицы
нулевой и матрица
не имеет обратной. При остальных же
значениях параметра
получается

Задача
3.
Найти жорданову форму матрицы
 в зависимости от значений параметра
в зависимости от значений параметра
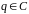 .
.

Решение.
Рассмотрим сначала
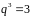 .
(Т.е.
.
(Т.е.
 )
В этом случае у матрицы
единственное собственное число
)
В этом случае у матрицы
единственное собственное число
 .
Заметим, что
.
Заметим, что
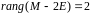 .
Таким образом, жорданова форма матрицы
– одна жорданова клетка с собственным
числом 2.
.
Таким образом, жорданова форма матрицы
– одна жорданова клетка с собственным
числом 2.
Пусть
теперь
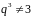 .
Тогда у матрицы
два собственных числа: 2 (кратности 2) и
.
Тогда у матрицы
два собственных числа: 2 (кратности 2) и
 (кратности 1). Вычислим ранг матрицы
(кратности 1). Вычислим ранг матрицы
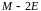 .
При
.
При
 ,
при
,
при
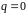 получаем, что
получаем, что
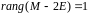 .
Поэтому:
.
Поэтому:
Ответ:
при
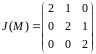 ;
при
;
при
 ;
при остальных
;
при остальных


2001/2002 Учебный год. Вариант 2.
Задача 1. Найти комплексные корни многочлена

Решение.
Заметим, что
 являются корнями этого многочлена.
являются корнями этого многочлена.
 .
Остальные корни
.
Остальные корни
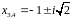
Задача
2.
Найти пересечение подпространств
и
 в
в
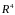 и исследовать зависимость ответа от
параметра
.
Здесь
– линейная оболочка множества
и исследовать зависимость ответа от
параметра
.
Здесь
– линейная оболочка множества
 ,
B – линейная оболочка множества
,
B – линейная оболочка множества


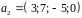
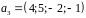
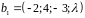


Решение.
Ищем пересечение подпространств, исходя
из условия
 .
Получаем:
.
Получаем:

При
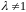 получаем
получаем
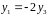 ,
поэтому пересечение
и
натягивается
на векторы
,
поэтому пересечение
и
натягивается
на векторы
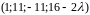 и
и
 .
(При
.
(При
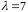 эти вектора совпадают).
эти вектора совпадают).
При
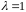 Получаем
Получаем
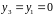 .
И пересечение подпространств
и
натягивается на вектор
.
.
И пересечение подпространств
и
натягивается на вектор
.
Ответ:
При
или
 ;
при
;
при

 .
.
Задача
3.
При каких значениях параметра
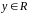 матрица
матрица
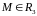 подобна диагональной?
подобна диагональной?
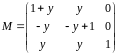
Решение.
Заметим, что у матрицы
собственное число
(кратности 3). Вычислим ранг матрицы
 .
При
.
При

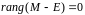 и жорданова форма просто матрица
и жорданова форма просто матрица
 ;
при
;
при

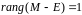 и жорданова форма недиагональна (состоит
из 2 жордановых клеток).
и жорданова форма недиагональна (состоит
из 2 жордановых клеток).
2001/2002 Учебный год. Вариант 3.
Задача 1. Найти комплексные корни многочлена

Ответ.

Задача 2. Найти матрицу и исследовать ее зависимость от параметра .

Решение.
Заметим, что при
 или
или
 матрица
вырождена и
не существует.
матрица
вырождена и
не существует.

Задача 3. Найти жорданову форму матрицы в зависимости от значений параметра .

Ответ.
при
 получается
получается
 ;
при
получается
;
при
получается
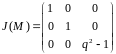 при
при
 получаем
получаем
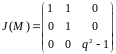
2001/2002 Учебный год. Вариант 4.
Задача 1. Найти комплексные корни многочлена

Ответ.
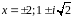 .
.
Задача 2. Найти пересечение подпространств и в и исследовать зависимость ответа от параметра . Здесь – линейная оболочка множества , – линейная оболочка множества

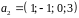



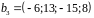
Ответ.
При
получаем
 ;
при
;
при
 ;
при
;
при
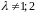 получаем
получаем

Задача 3. При каких значениях параметра матрица подобна диагональной?
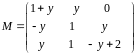
Ответ: жорданова форма диагональна тогда и только тогда, когда . Решение аналогично задаче 3 варианта 2 этого же года.
