2000/2001 Учебный год. Вариант 2.
Задача
11.
Привести квадратичную форму
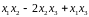к каноническому виду и указать линейное
отображение, осуществляющее это
преобразование.
Решение аналогично решению задачи 11 в варианте 1.
Ответ:
Канонический вид квадратичной формы:
.
Отображение осуществляется по формулам:
Задача
12.
Доказать, что для любой матрицы
имеет место разложение
где
и
– матрица, транспортированная к
Решение.
Мы знаем, что
.
Кроме того,
.
Поэтому
и
.
(Потому что
).
Получаем,
что
.
Осталось доказать, что
.
(В таком случае, сумма будет прямой, а
из соотношения на размерности, она будет
равна всему пространству).
Предположим,
что пересечение не пусто. Т.е. есть
какой-то вектор вида
,
который зануляется матрицей
.
Т.е. существует
,
такой что
.
Рассмотрим
скалярное произведение
,
положив естественный базис ортонормированным.
Тогда скалярное произведение произвольных
векторов
,
вычисляется по формуле
.
Получаем
.
А отсюда следует, что вектор нулевой. Следовательно, пересечение нулевое. Что и требовалось доказать.
Ремарка.
Если в данной задаче поле вещественных
чисел заменить на произвольное кольцо 
,
то утверждение задачи станет неверным.
Например, рассмотрим в кольце
матрицу
.
Она нильпотентна ступени 2 (т.е.
);
она симметрична, т.е.
.
Возьмем вектор
.
Он лежит и в образе, и в ядре. Таким
образом, ядро и образ не пересекаются
по нулю и их сумма – не прямая.
2000/2001 Учебный год. Вариант 3.
Задача
11.
Привести квадратичную форму
к каноническому виду и указать линейное
отображение, осуществляющее это
преобразование.
Ответ.
Канонический вид квадратичной формы:
.
Отображение осуществляется по формулам:
Задача
12.
Пусть
и
Доказать, что
где
–
след
Решение.
Напомним, что характеристика поля может
быть только простым числом (т.е.
– простое число). Заметим, что биномиальные
коэффициенты
делятся на
при
.
Вычислим
Средние
члены занулились, так как
;
в конце мы написали знак “”,
потому что при нечетных
там действительно знак “”,
а при четных
(т.е. при
)
это одинаково.
Поскольку
характеристический многочлен для
матрицы
,
то коэффициент при
равен
.
Т.е.
это коэффициент при
в многочлене
.
По теореме о произведении определителей
.
Характеристический многочлен для
матрицы
,
т.е.
возводим в степень
.
Поскольку
– это характеристика, то для любых
элементов поля верно, что
(нетрудно доказать индукцией по количеству
слагаемых). Поэтому
Поскольку
,
коэффициент при
в многочлене
равен
.
Сравнивая две части, получаем
2000/2001 Учебный год. Вариант 4.
Задача
11.
Привести
квадратичную форму
к каноническому виду и указать линейное
отображение, осуществляющее это
преобразование.
Ответ.
Канонический вид квадратичной формы:
.
Отображение осуществляется по формулам:
Задача
12.
Вычислить определитель
Решение. Вычтем первую строку из всех остальных.
Разложим по последней строке. Потом один из получившихся определителей аналогичен исходному, а другой разложим по последнему столбцу. Получим:
С
учетом того, что
,
используя метод мат.индукции не трудно
доказать, что
