Года: 97/98, 98/99, 99/00, 00/01, 01/02, 02/03, 03/04.
1997/1998 Учебный год. Вариант 1.
Задача 7. Привести матрицу к жордановой форме и определить её жорданов базис
Решение. Для начала найдем собственные числа.
Поэтому
собственные числа:
.
Значит, жорданова форма:
Найдем собственный вектор собственного числа 4:
Получаем:
.
Возьмем
.
Найдем
собственные вектора чисел
:
Получаем:
Возьмем
Задача
8.
Решить матричное уравнение
,
где
,
,
.
Решение.
X=A-1CB-1.
Получаем:
.
1997/1998 Учебный год. Вариант 2.
Задача 7. Привести матрицу к жордановой форме и определить её жорданов базис
Решение. Вычислим собственные числа:
Собственные
числа
и
.
Вычислим ранг матрицы
,
чтобы определить, сколько жордановых
клеток с числом
:
.
Поэтому
жорданова форма
.
Найдем
из условия
;
.
Например,
.
Тогда
.
Найдем
из условия
.
Например,
.
Задача
8.
Решить матричное уравнение
,
где
,
.
Решение.
.
Тогда
.
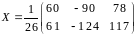1997/1998 учебный год. Вариант 3.
Задача 7. Привести матрицу к жордановой форме и определить её жорданов базис
Решение аналогично другим вариантам, приведем только ответ.
;
.
Задача 8. Решить матричное уравнение , где
,
,
.
Решение.
.
1997/1998 учебный год. Вариант 4.
Задача 7. Привести матрицу к жордановой форме и определить её жорданов базис
Решение аналогично предыдущим вариантам, приведем только ответ.
Форма:
Базис:
.
Задача
8.
Решить матричное уравнение
,
где
,
.
Ответ:
1997/1998 учебный год. Вариант 5.
Задача 7. Привести матрицу к жордановой форме и определить её жорданов базис
Решение аналогично предыдущим вариантам. Приведем только ответ.
Форма:
.
Базис:
.
Задача
8.
Решить матричное уравнение
,
где
,
.
Ответ.
1998/1999 учебный год. Вариант 1.
Задача
3.
Решить систему уравнений: 
Решение.
Умножим справа первое уравнение на
матрицу
;
второе на
(обратные к матрицам при Х). Получим:
Вычитаем
из второго первое и получаем:
.
Умножаем справа это равенство на матрицу
.
Получим:
.
Из первого уравнения выражаем
.
Получаем:
.
Задача
4.
Найти наибольший общий делитель
многочленов
Решение.
Задача
5.
Построить ортогональный базис линейного
подпространства, порожденного системой
векторов
,
,
.
Решение. Воспользуемся процессом ортогонализации.
1998/1999 учебный год. Вариант 2.
Задача
3.
Решить систему уравнений: 
Ответ.
.
Задача
4.
Найти наибольший общий делитель
многочленов
Ответ.
.
Задача
5.
Построить ортогональный базис линейного
подпространства, порожденного системой
векторов
,
,
.
Ответ.
.
1998/1999 учебный год. Вариант 3.
Задача
3.
Решить систему уравнений: 
Ответ.
.
Задача
4.
Найти наибольший общий делитель
многочленов
Ответ.
.
Задача
5.
Построить ортогональный базис линейного
подпространства, порожденного системой
векторов
,
,
.
Ответ:
,
,
.
1998/1999 учебный год. Вариант 4.
Задача
3.
Решить
систему уравнений: 
Ответ.
.
Задача
4.
Найти наибольший общий делитель
многочленов
Ответ.
.
Задача
5.
Построить ортогональный базис линейного
подпространства, порожденного системой
векторов
,
,
.
Ответ.
,
,
.
1998/1999 учебный год. Вариант 5.
Задача
3.
Решить
систему уравнений: 
Ответ.
.
Задача
4.
Найти наибольший общий делитель
многочленов
Ответ.
.
Задача
5.
Построить ортогональный базис линейного
подпространства, порожденного системой
векторов
,
,
.
Ответ.
,
,
.
1998/1999 учебный год. Вариант 6.
Задача
3.
Решить
систему уравнений: 
Ответ.
.
Задача
4.
Найти наибольший общий делитель
многочленов
Ответ.
.
Задача
5.
Построить ортогональный базис линейного
подпространства, порожденного системой
векторов
,
,
.
Ответ:
,
,
.
1999/2000 учебный год. Вариант 1.
Задача
3.
Многочлен
делится без остатка на
;
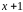а при делении на
дает в остатке
.
Найти остаток от деления многочлена
на многочлен
.
Решение.
Мы знаем, что
и что
.
Пусть
.
Найдем
.
.
.
Получаем
;
.
Ответ:
остаток
.
Задача
4.
Число
является корнем уравнения
,
.
Найти значение
и решить уравнение над полем комплексных
чисел.
Решение.
Преобразуем число
в более простой вид.
Из
условия, что
является корнем многочлена, получаем:
.
Получаем
;
Заметим, что
– постороннее значение, поскольку
– действительное число.
Решим
уравнение
.
Получаем
.
Решения:
.
Задача 5. Исследовать систему и найти общее решение в зависимости от параметра .
Решение.
При
получаем единственное уравнение
.
При
получаем
Получаем
при
система несовместна; а при
решение единственно:
Ответ:
При
система не совместна;
при
;
при
,