6.2. Переходные процессы в цепях с двумя накопителями энергии

Цель

1. Исследование переходного процесса, вызванного разрядом конденсатора через последовательно соединенные резистор и катушку индуктивности, при комплексных сопряженных корнях характеристического уравнения.

2. Исследование переходного процесса, вызванного разрядом конденсатора через последовательно соединенные резистор и катушку индуктивности, при действительных отрицательных корнях характеристического уравнения.

Приборы и элементы

3. Осциллограф.

4. Источник постоянного напряжения.

5. Резистор.

6. Конденсатор.

7. Катушка индуктивности.

Краткие теоретические сведения

Переходный процесс при подключении заряженного конденсатора емкостью С к последовательно соединенной цепи из резистора c сопротивлением R и катушки c индуктивностью L может быть описан с помощью следующего уравнения

L ∙ C ∙ + R ∙ C ∙ + i = 0,

где i – ток в цепи.

Если корни характеристического уравнения, полученного путем замены в данном уравнении на р обозначений производных тока цепи,

L ∙ C ∙ p² + R ∙ C ∙ p + 1 = 0

являются комплексными сопряженными:

р_1,2 = ̶ δ = ̶ δ ϳ ∙ ,

где δ = R / (2 ∙ L) – коэффициент затухания;

– частота собственных колебаний;

частота свободных колебаний,

то переходный процесс будет иметь колебательный затухающий характер:

Решением уравнения, описывающего данный переходный процесс, является следующее выражение

i = ̶

где – начальное напряжение на конденсаторе.

Выражение для напряжения на конденсаторе при колебательном затухающем характере переходного процесса имеет вид

u_C = 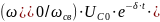sin( ,

где - начальное напряжение на конденсаторе;

ⱷ = arctg( / δ).

Апериодический переходный процесс, происходящий при разряде конденсатора на последовательно соединенную RL-цепь, описывается тем же линейным дифференциальным уравнением второго порядка, что и колебательный затухающий. Однако оба корня его характеристического уравнения будут действительными отрицательными:

p_1,2 = ̶ δ β,

где β =

При этом решение названного дифференциального уравнения выглядит таким образом:

i = ̶ ̶ ).

Напряжение на конденсаторе при апериодическом характере переходного процесса изменяется по закону:

u = ̶ ).

Порядок проведения экспериментов

Эксперимент 1. Исследование переходного процесса, вызванного разрядом конденсатора через последовательно соединенные резистор и катушку индуктивности, при комплексных сопряженных корнях характеристического уравнения

Соберите схему, которая приведена на рис. 6. 3.

Рис. 6. 3. Схема для исследования переходного процесса, вызванного разрядом конденсатора через последовательно соединенные резистор и катушку индуктивности, при комплексных сопряженных корнях характеристического уравнения

Включите процесс моделирования переходного процесса. С помощью двойного щелчка ЛКМ на знаке осциллографа добейтесь расширенного его изображения. Установите следующие настройки осциллографа: по горизонтали – 0,5 мс / дел., по вертикали – 2 В / дел. Зарисуйте кривую переходного процесса и занесите результаты моделирования в табл. 6. 5.

Таблица 6. 5

Результаты исследований переходного процесса при разряде конденсатора на последовательно соединенную цепь из резистора и катушки индуктивности при комплексных сопряженных корнях характеристического уравнения

Время, мкс	i, A, экспериментальный	i, A, расчетный
50
100
150
200
250
300
350
400
450

Вычислите значения тока в данной цепи при разряде конденсатора в моменты времени, указанные в табл. 6. 5, и запишите их в соответствующую строку этой таблицы. Сравните результаты эксперимента и расчета.

Эксперимент 2. Исследование переходного процесса, вызванного разрядом конденсатора через последовательно соединенные резистор и катушку индуктивности, при действительных отрицательных корнях характеристического уравнения

Соберите схему, которая приведена на рис. 6. 4.

Рис. 6. 4. Схема для исследования переходного процесса, вызванного разрядом конденсатора через последовательно соединенные резистор и катушку индуктивности, при двух действительных отрицательных корнях характеристического уравнения

Включите процесс моделирования. С помощью двойного щелчка ЛКМ на знаке осциллографа добейтесь расширенного его изображения. Установите следующие настройки осциллографа: по горизонтали – 0,5 мс / дел., по вертикали – 5 В / дел. Зарисуйте кривую переходного процесса и занесите результаты моделирования в табл. 6. 6. При измерениях тока и напряжения на экране осциллографа для повышения точности используйте визиры.

Таблица 6. 6

Результаты исследований переходного процесса при разряде конденсатора на последовательно соединенную цепь из резистора и катушки индуктивности при действительных отрицательных корнях характеристического уравнения

Время, мкс	i, A, экспериментальный	i, A, расчетный
50
100
150
200
250
300
350
400
450

Вычислите значения тока в данной цепи при разряде конденсатора в моменты времени, указанные в табл. 6. 6, и запишите их в соответствующую строку этой таблицы. Сравните результаты эксперимента и расчета.