Ділення з відновленням залишку
Алгоритм ділення модулів чисел з відновленням остач полягає у виконанні таких дій.
1. Подвоїти модуль діленого .
2. Відняти від подвоєного модуля діленого модуль дільника. Одержана різниця є першою остачею.
3. Проаналізувати знак остачі R. Якщо , то черговому розряду частки присвоїти цифру 1 і перейти до п. 5; якщо ж R < 0, то черговому розряду частки присвоїти цифру 0.
4. Відновити остачу, додавши модуль
дільника
.
5. Подвоїти остачу.
6. Визначити чергову остачу, віднявши від попередньої остачі модуль дільника.
Перейти до п. 3.
П. 3 - п. 6 виконувати до одержання всіх необхідних цифр частки.
За своїм характером операція ділення відноситься до операцій, що дають не завжди точний результат, тому ознакою закінчення операції ділення може бути досягнення заданої точності. Якщо в процесі ділення одержується остача R = 0, то операція зупиняється й у решту розрядів частки записується нуль. Звичайно формальною ознакою кінця операції ділення є одержання такої самої кількості розрядів у частці, яку мають операнди.
Подвоєння діленого та остачі практично виконується шляхом зсуву коду вліво на один розряд.
Приклад 1. Поділити число А = - 0, 10100 на число В = 0, 11011, використовуючи метод ділення з відновленням остач.
Розв'язання. Для даних чисел маємо:
=1;
= 0, 10100;
=0;
= 0, 11011. Визначаємо знак частки:
=1
0=1.
Віднімання будемо виконувати як додавання
додаткових кодів, тому
=
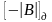1,00101.
Усі дії, що виконуються в процесі ділення, наведені в табл. 1.
Відповідь: С= - 0, 10111.
З наведеного прикладу випливає, що цифри частки є інверсними значеннями знакових розрядів чергових остач. Треба також відзначити, що результат подвоєння іноді може бути > 1. Однак таке переповнення розрядної сітки усувається на наступному кроці алгоритму, оскільки після подвоєння завжди виконується віднімання.
Основні недоліки розглянутого методу ділення такі:
аритмічність процесу ділення, яка обумовлена нерегулярністю виконання відновлення остачі, що призводить до ускладнення блоку керування діленням;
відносно мала швидкість ділення, оскільки в середньому для половини кроків потрібно виконувати додаткове додавання, що забезпечує відновлення остач.
Для ритмізації процесу ділення можна виконувати фіктивну дію у тих випадках, коли відновлення остачі не потрібне, що призведе до збільшення часу виконання операції. Разом з тим, операцію можна спростити, якщо відмовитись від відновлення остач.
Таблиця .1 - Приклад ділення з відновленням остач
Тема 1.2. Виконання арифметичних операцій над числами з плаваючою комою (пк)
Лекція №3с. Множення, ділення чисел з плаваючою комою
Множення чисел з плаваючою комою
Для чисел
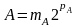і
,
що представлені в формі з ПК, добуток
обчислюється за формулою:
,
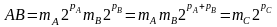де
,
.
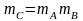Звідси випливає, що процес множення складається з чотирьох етапів:
множення мантис;
додавання порядків;
нормалізація й округлення мантиси добутку;
корегування порядку добутку.
Перші два етапи можуть виконуватись одночасно, оскільки вони незалежні один від одного. При цьому множення мантис може бути здійснене будь-яким з розглянутих методів множення.
У загальному випадку результат множення мантис може бути одержаний в ненормалізованій формі. Причому порушення нормалізації можливо тільки зліва. Воно усувається шляхом зсуву коду мантиси на один розряд вліво і, відповідно, корегується порядок добутку шляхом віднімання одиниці від суми порядків. Округлення мантиси здійснюється додаванням одиниці до (п+1)-го розряду.
Під час виконання операції множення чисел з плаваючою комою можуть мати місце такі особливі випадки.
Якщо порядок результату є найбільшим від'ємним числом, то необхідно формувати машинний нуль.
Коли виникає переповнення додатного порядку і воно не усувається після нормалізації і корегування порядку, то необхідно формувати ознаку переповнення порядку.
Ці особливі випадки можна передбачити в алгоритмі операції множення введенням корегування добутку на підставі ознак результату.
Особливості ділення чисел з плаваючою комою
Для чисел і , що представлені в формі з плаваючою комою, частка визначається за формулою:
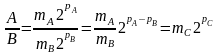
де
,
.
Звідси випливає, що процес ділення складається з чотирьох етапів:
ділення мантис;
віднімання порядків;
нормалізація мантиси частки;
корегування порядку частки.
Перші два етапи можуть виконуватись
одночасно, оскільки вони незалежні один
від одного. При цьому ділення мантис
повністю співпадає з діленням чисел,
що представлені в формі з фіксованою
комою. Відміна полягає лише в тому, що
мантиси операндів можуть співвідноситись
одна з одною довільно. Оскільки мантиси
діленого і дільника - нормалізовані
числа, то можливі такі випадки:
;
.
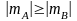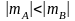Коли мантиса діленого більше або дорівнює мантисі дільника, то на початку ділення одержується цифра частки, що дорівнює 1 і яка записується в цілу частину частки. Решта дій над мантисами аналогічні діям над числами, що представлені в формі з фіксованою комою. Одержана при цьому мантиса частки буде мати порушення нормалізації праворуч. Воно усувається шляхом зсуву коду мантиси на один розряд управо і, відповідно, корегується порядок частки шляхом додавання одиниці до різниці порядків.
Коли мантиса діленого менше мантиси дільника, то на початку ділення одержується цифра частки, що дорівнює 0 і яка записується в цілу частину частки. Далі ділення мантис продовжується за правилами ділення чисел, що представлені в формі з фіксованою комою. Одержана при цьому мантиса частки буде мати нормалізовану форму.
Під час виконання операції ділення чисел з плаваючою комою можуть мати місце такі особливі випадки.
Якщо дільник дорівнює нулю, то формується сигнал "Зупинка машини".
Оскільки в процесі ділення порядки віднімаються, то можливе переповнення розрядної сітки порядків. Коли виникає переповнення в бік від'ємних значень порядку і воно не усувається після нормалізації і корегування порядку, то мантисі результату приписується машинний нуль, а порядку - найбільше від'ємне число.
У разі переповнення додатного порядку необхідно формувати ознаку переповнення порядку.
Ці особливі випадки можна передбачити в алгоритмі операції ділення введенням аналізатора дільника на нуль і корегування частки на підставі ознак результату.