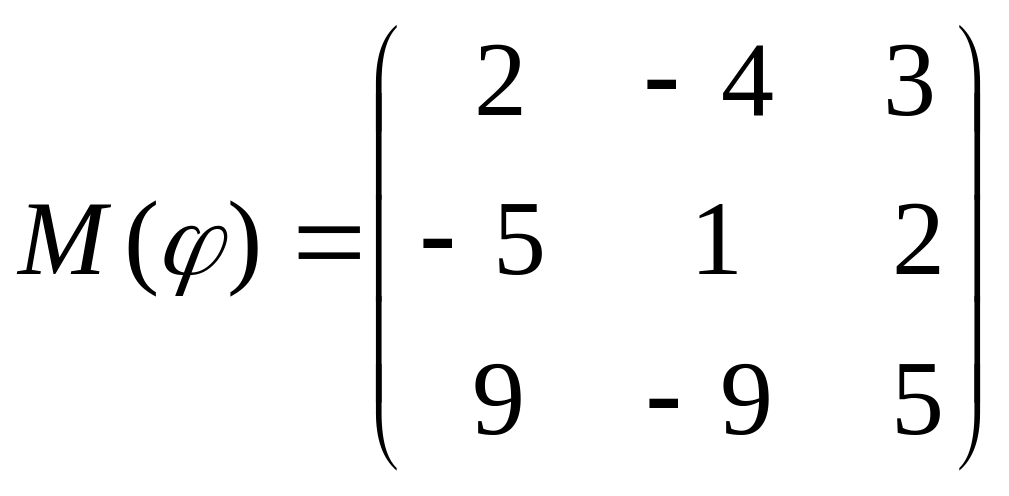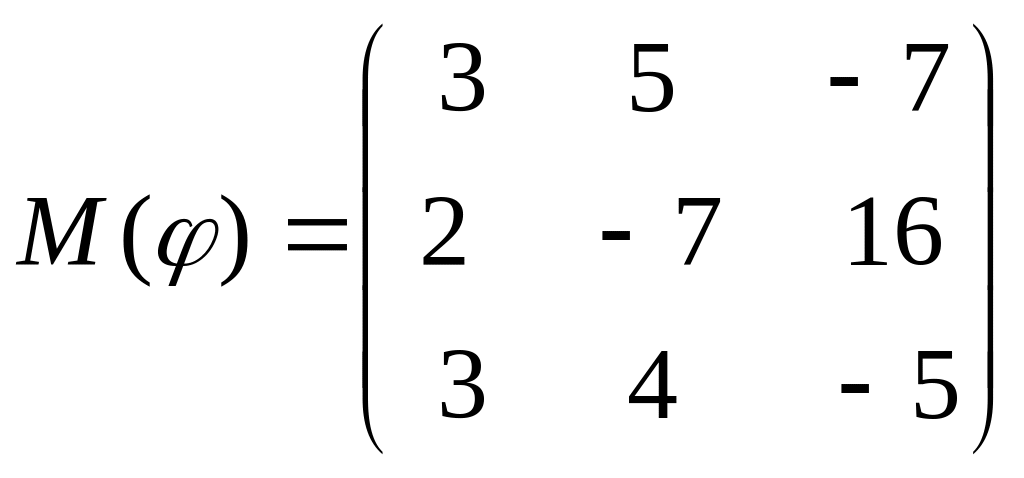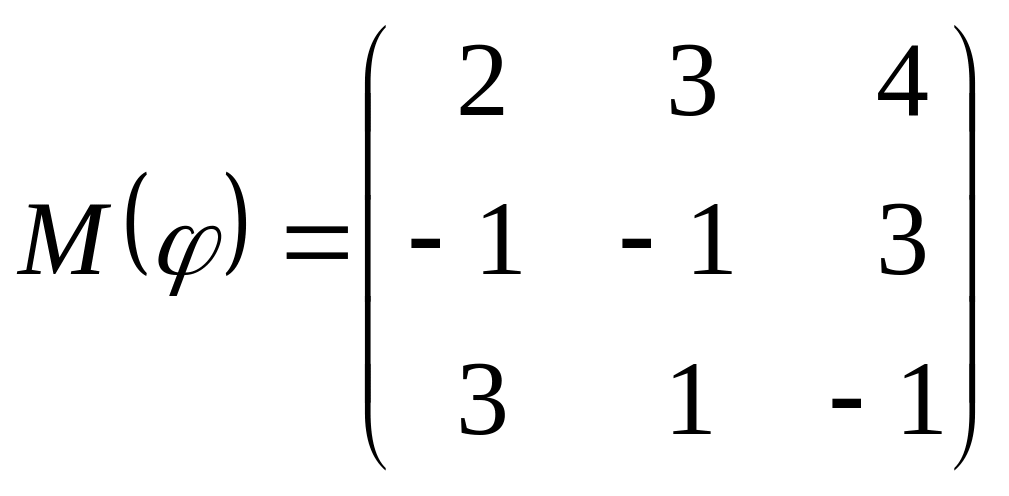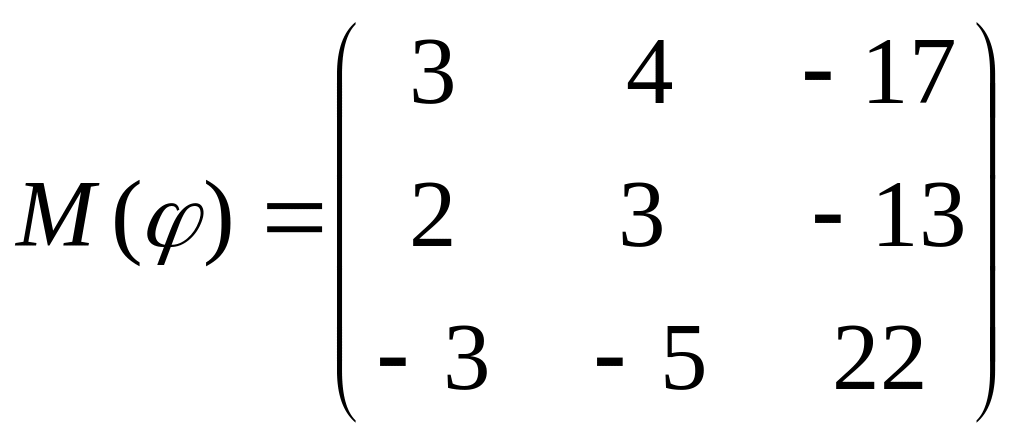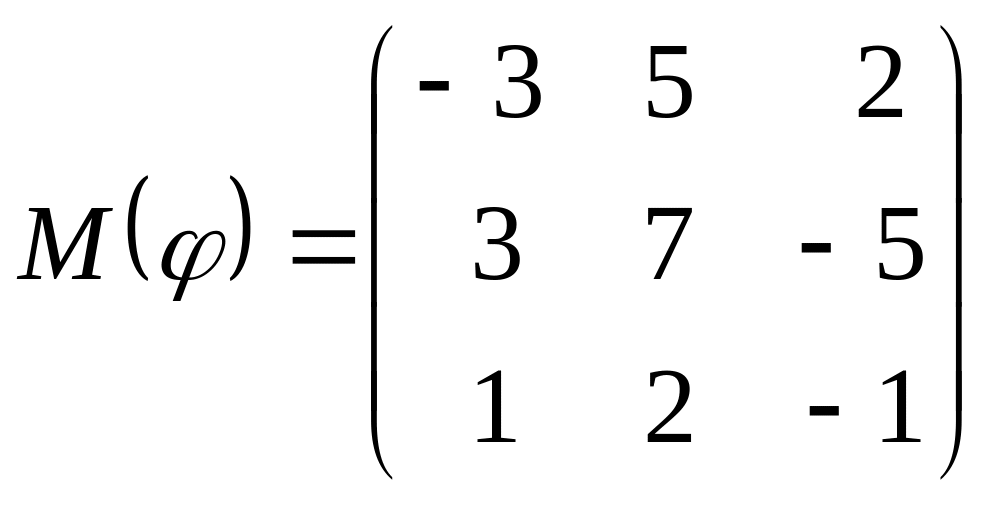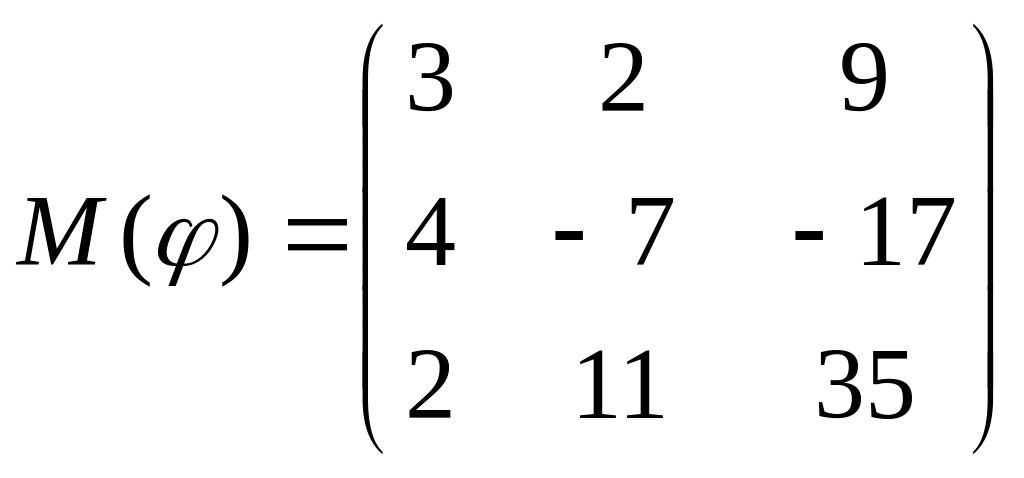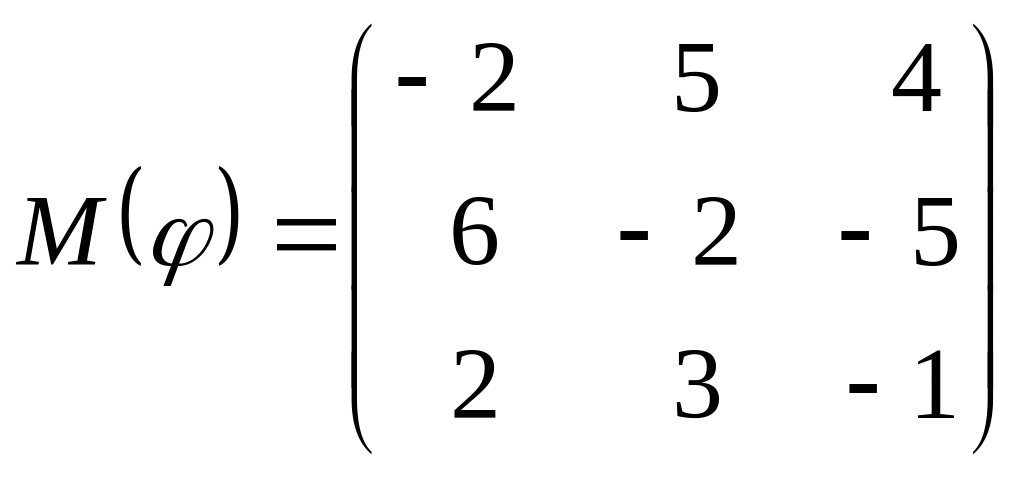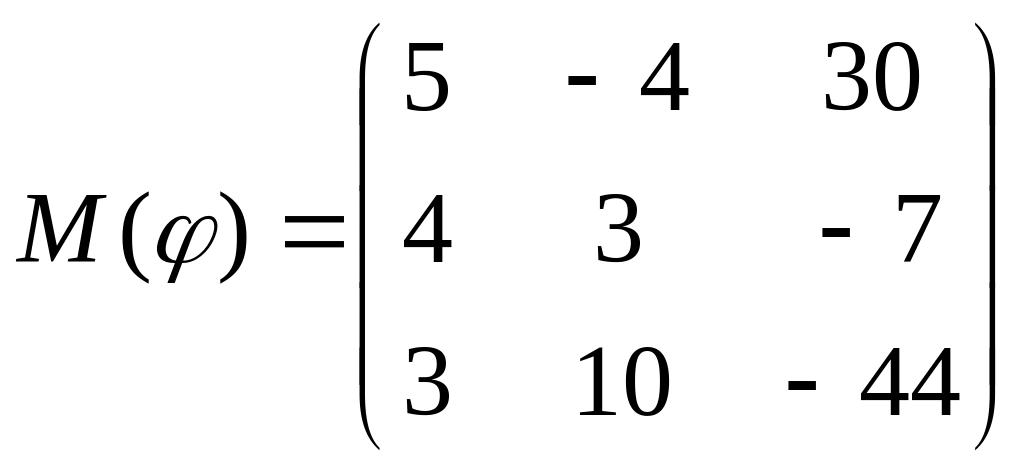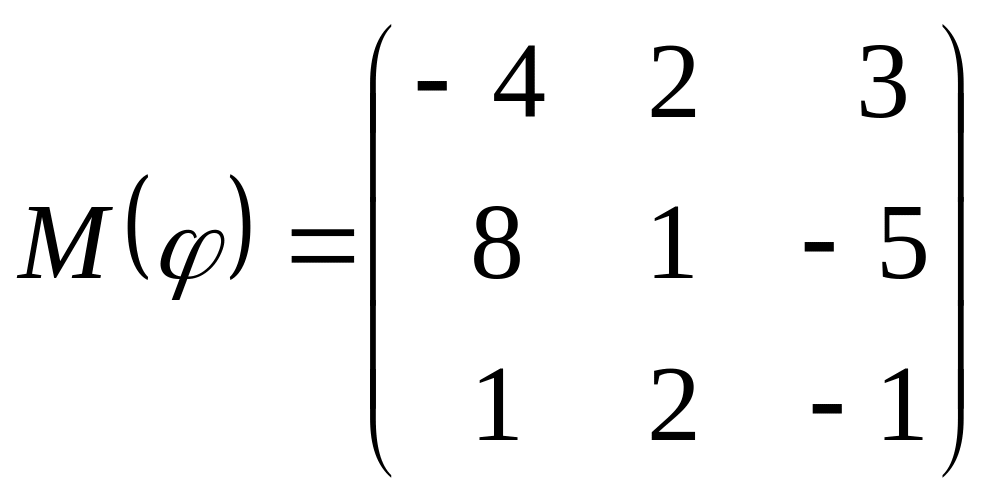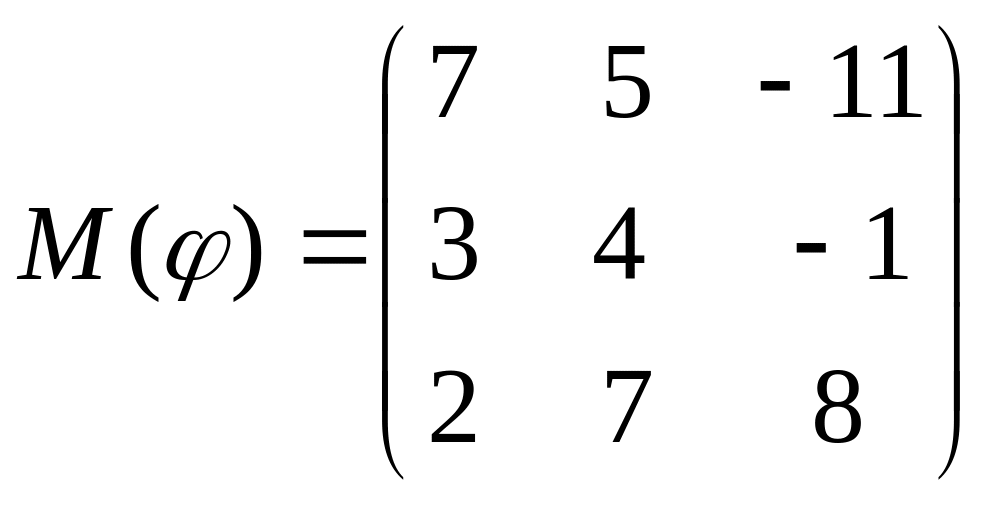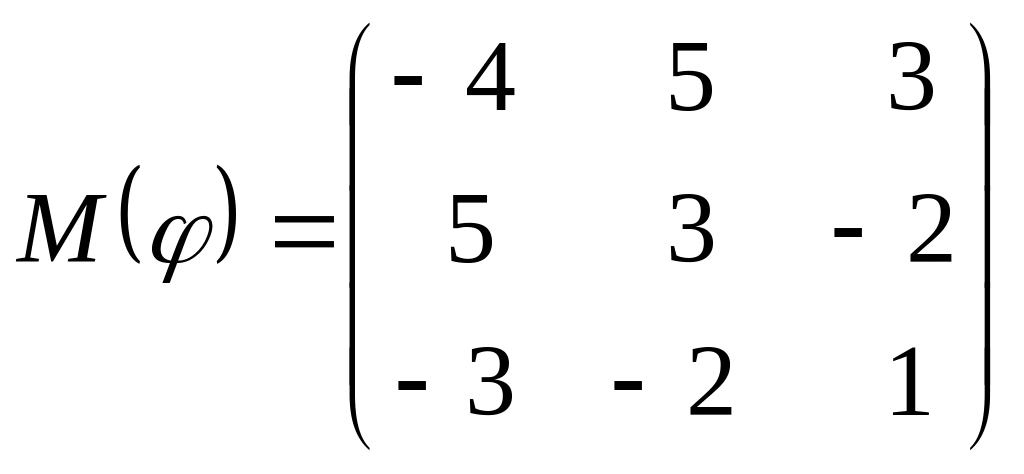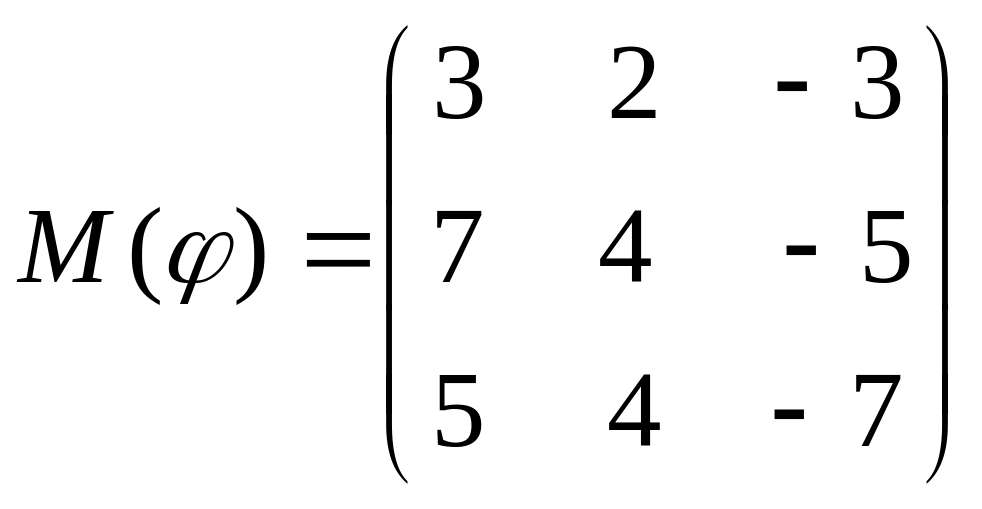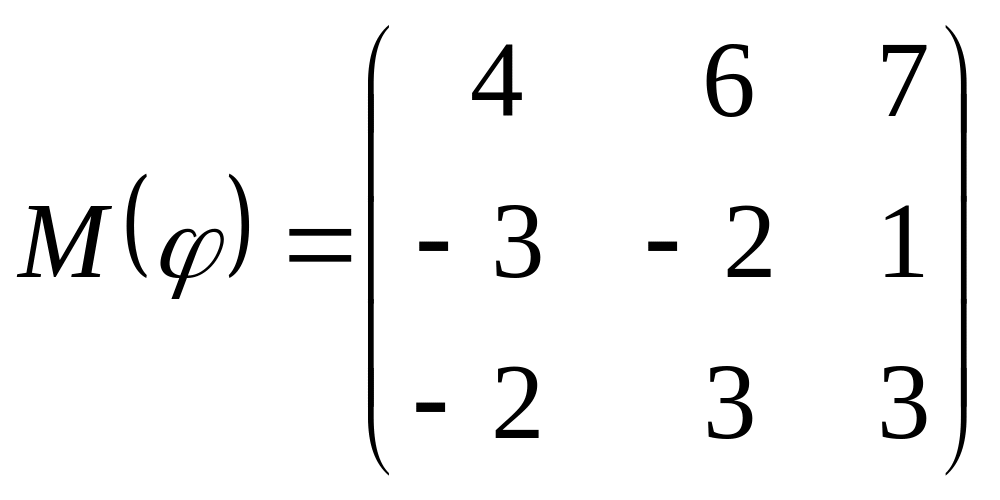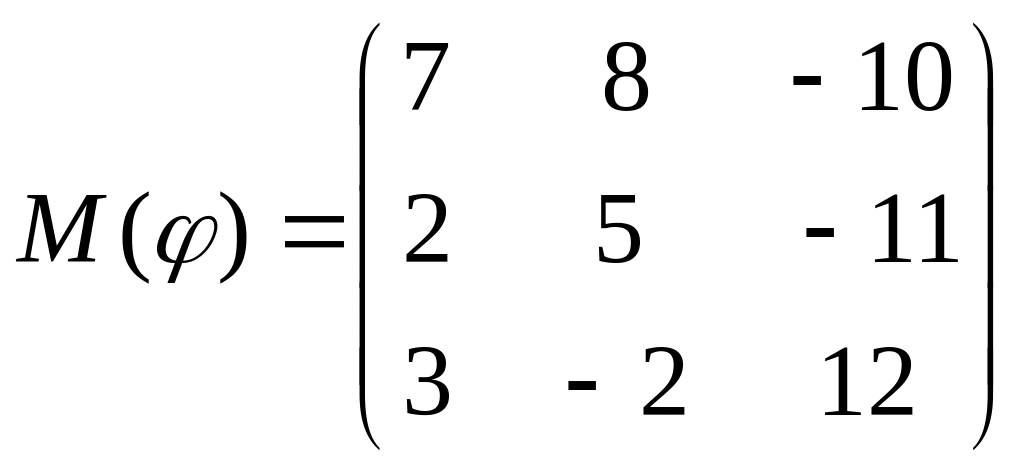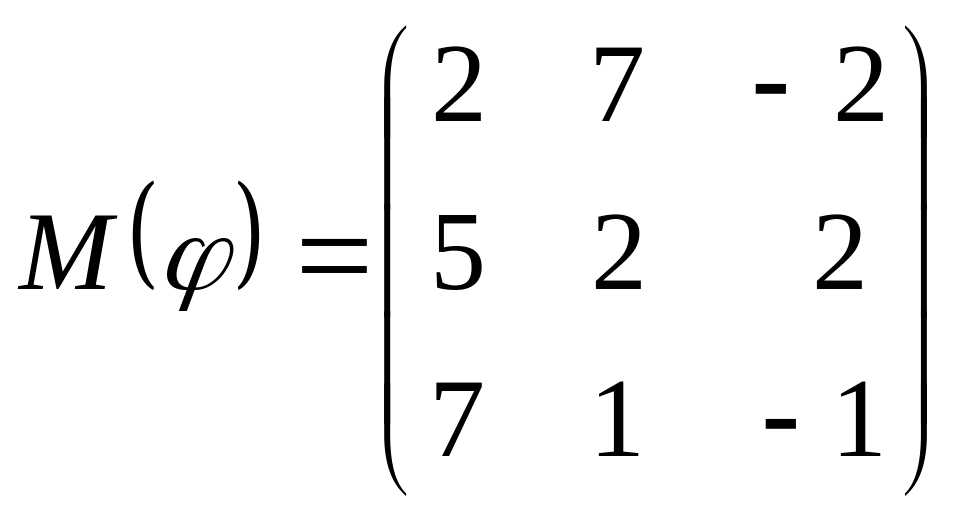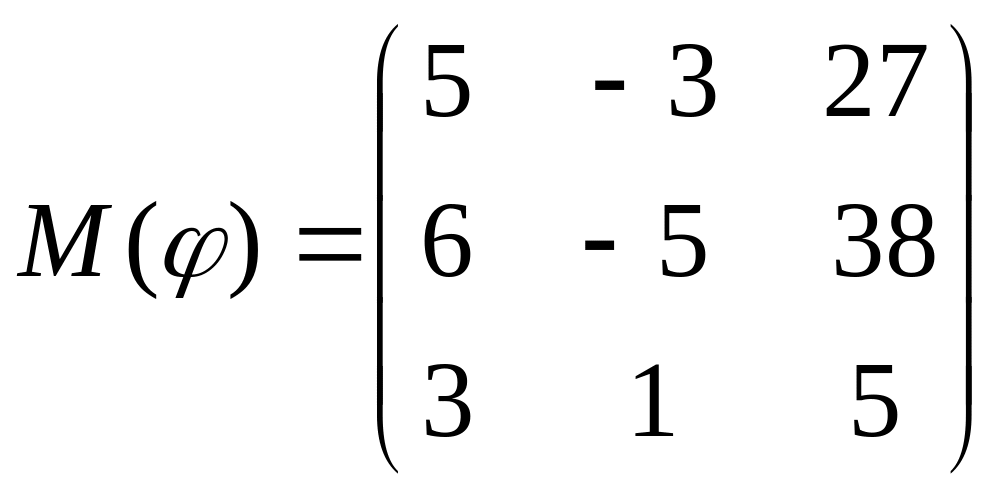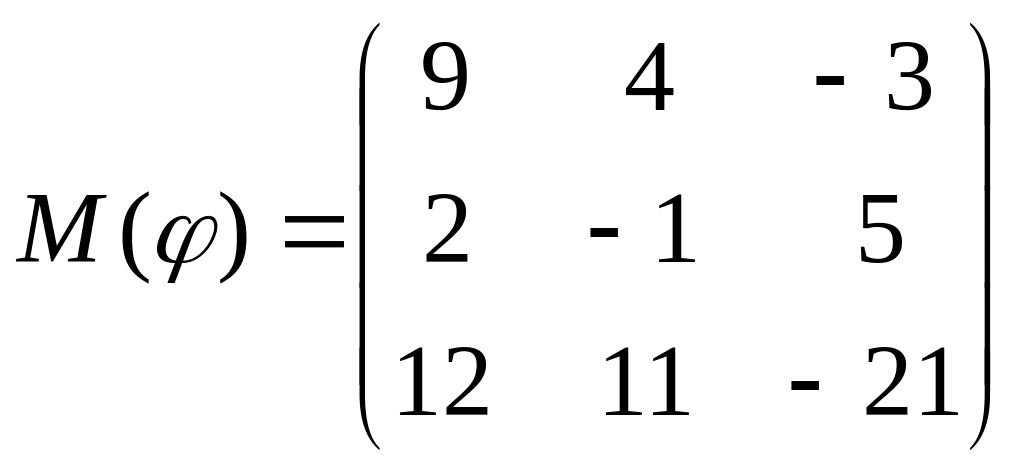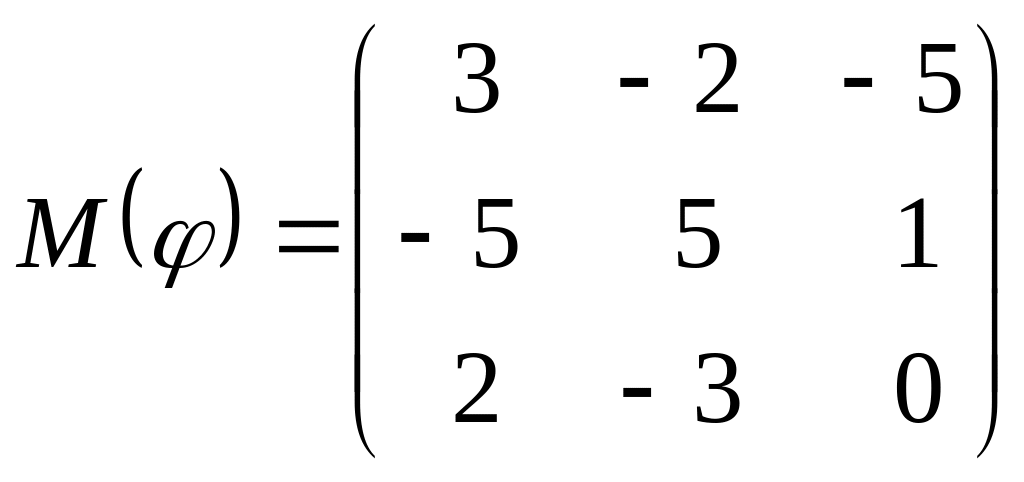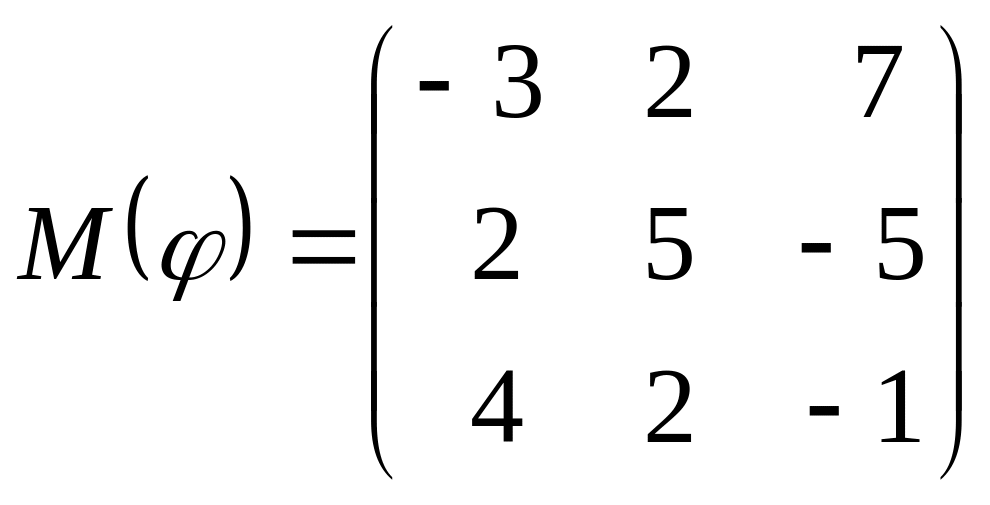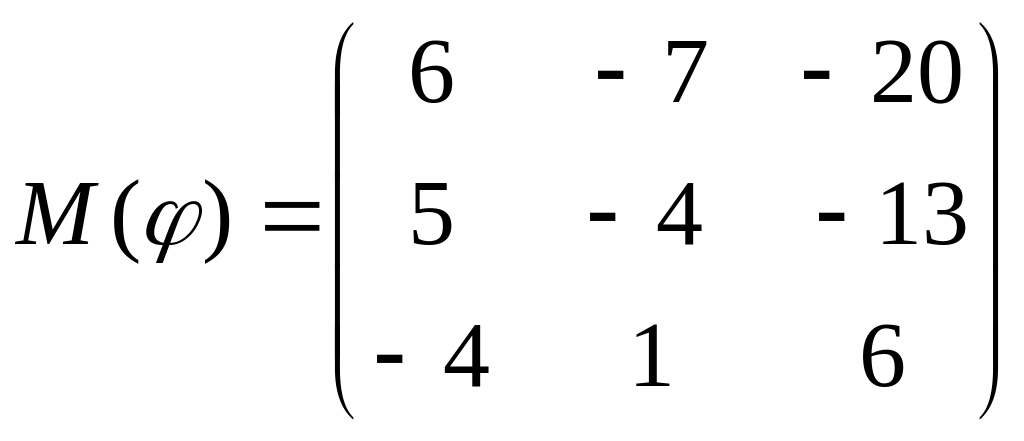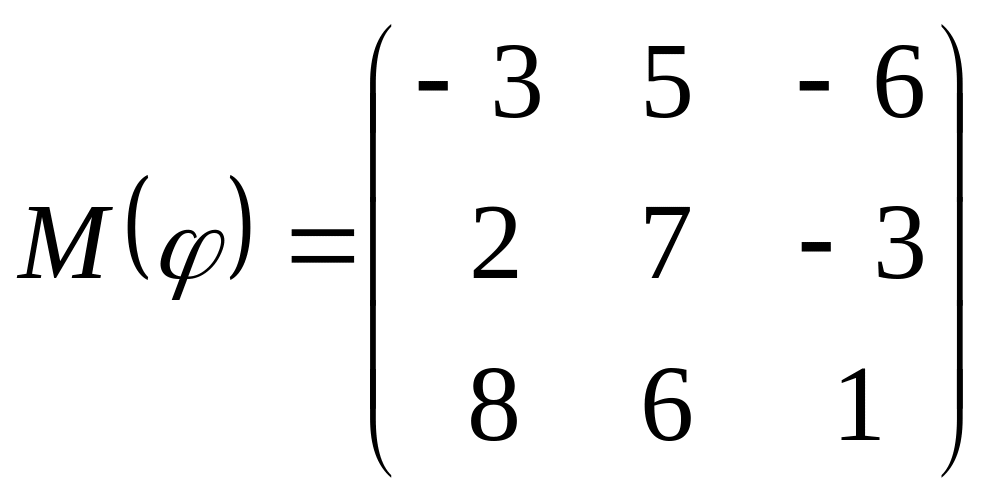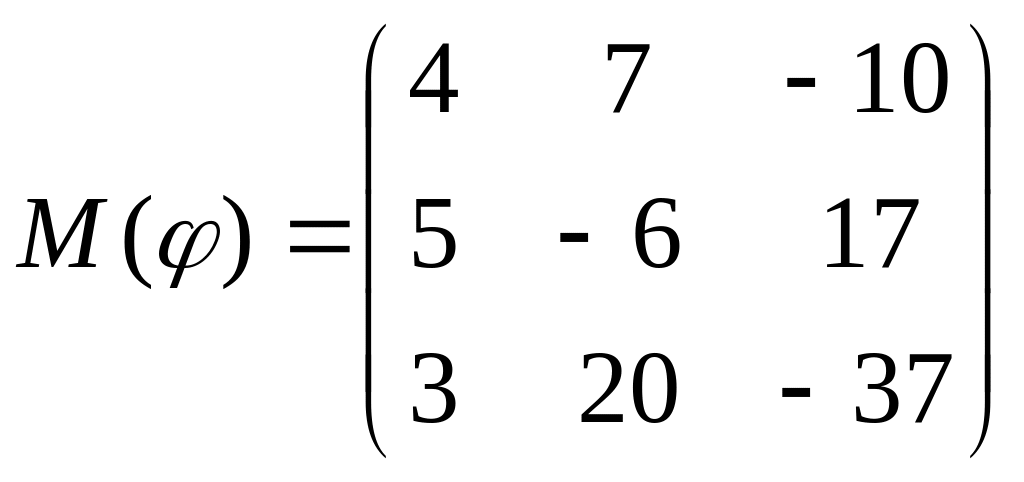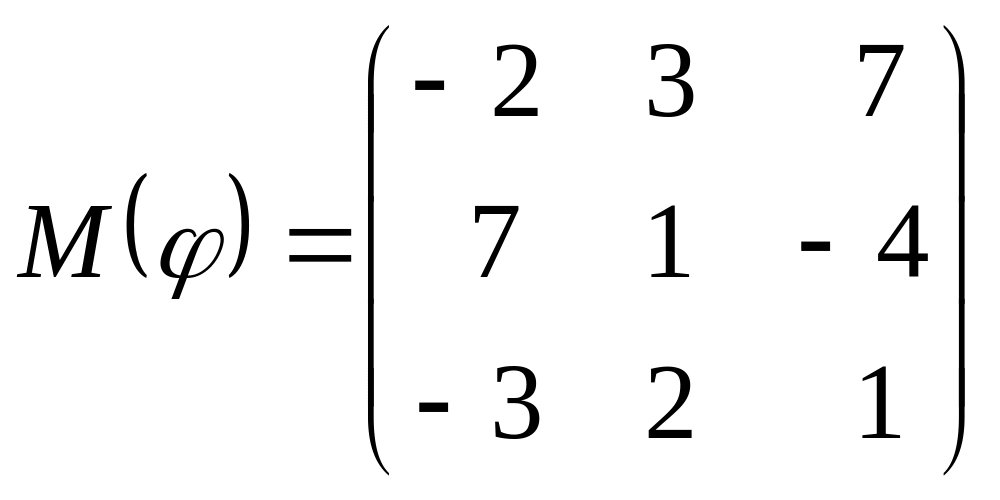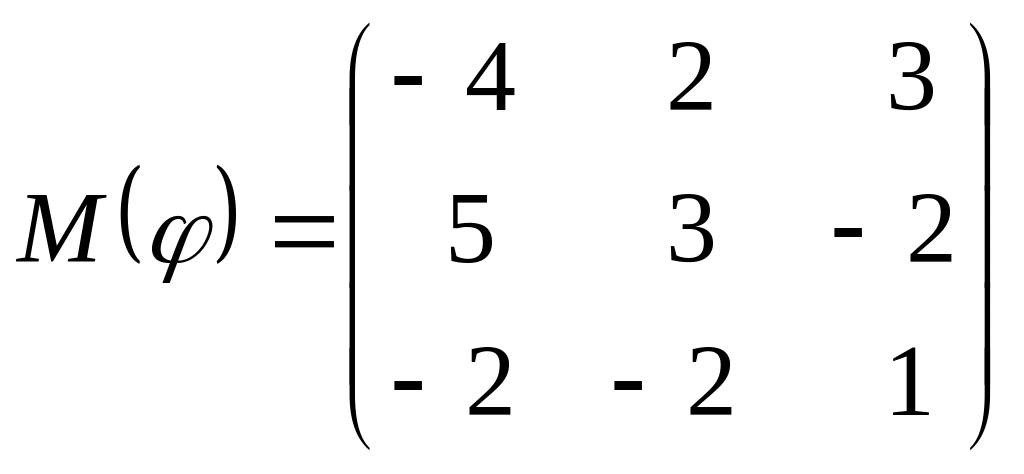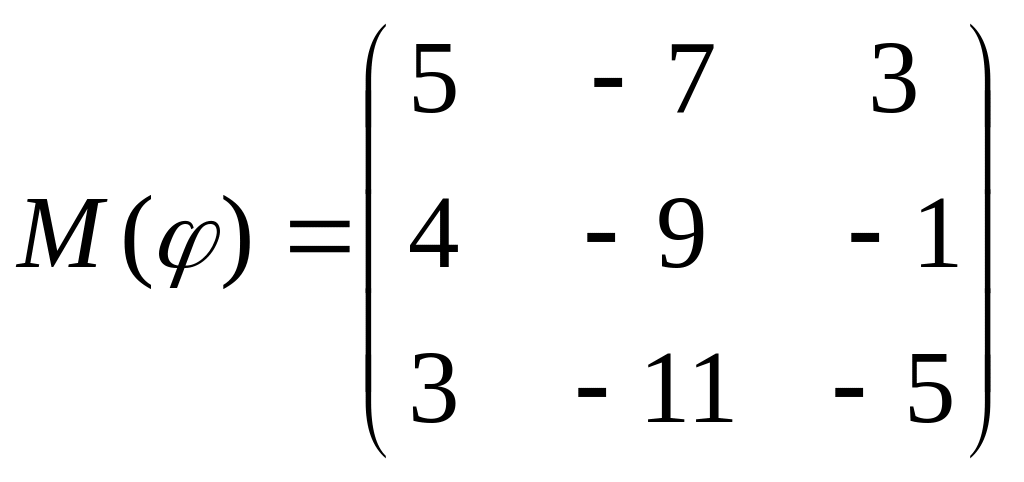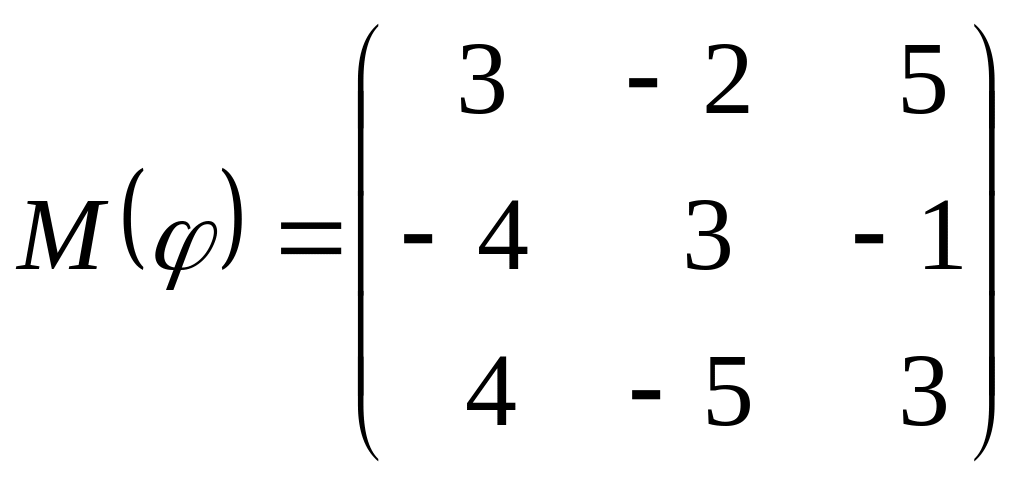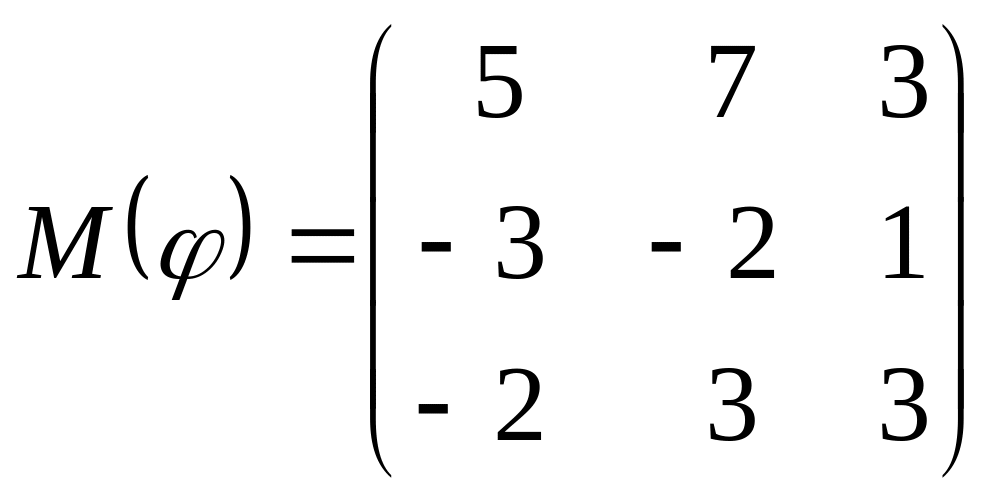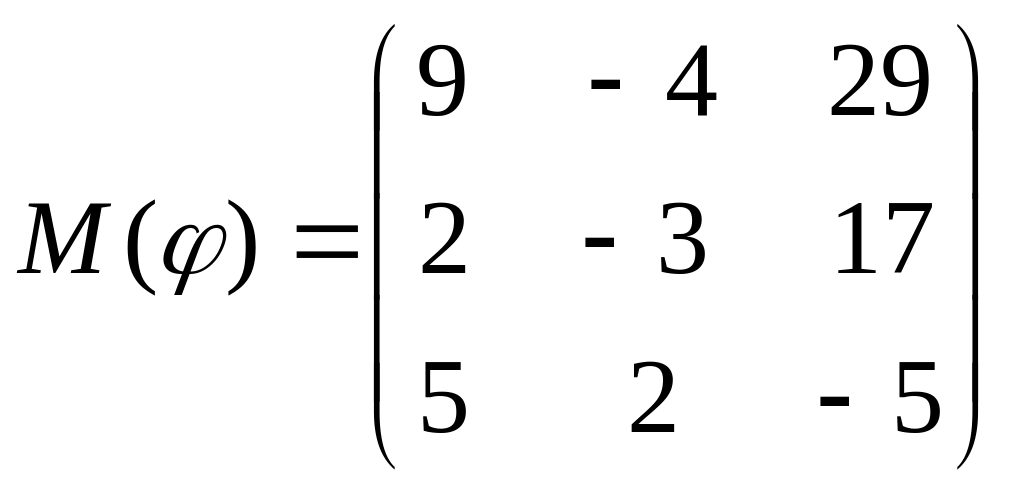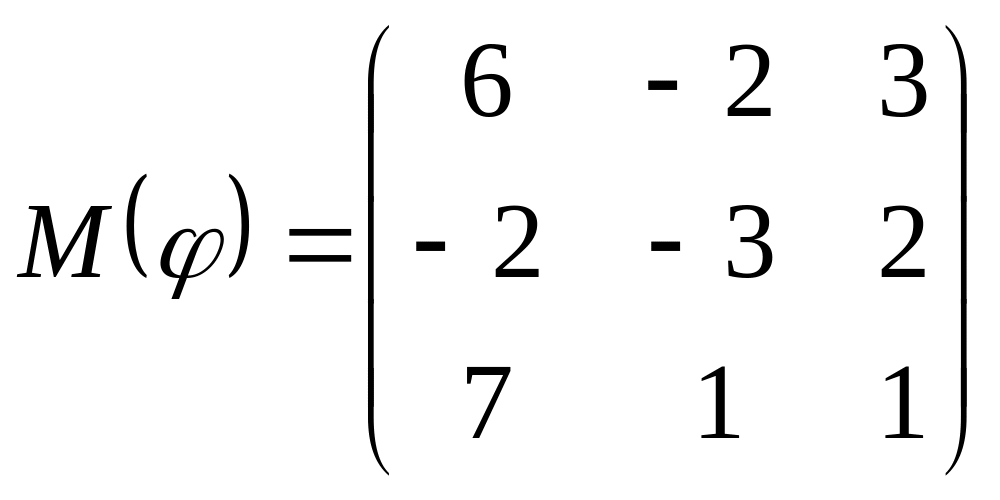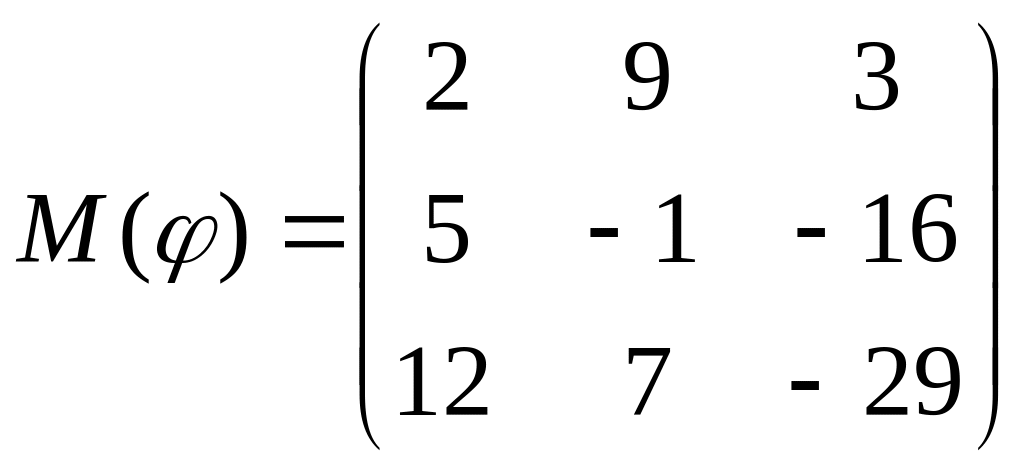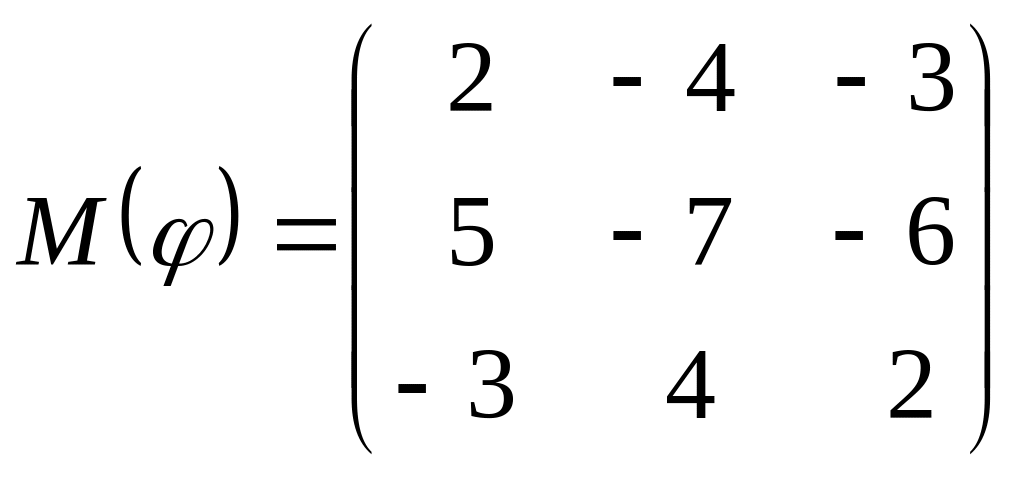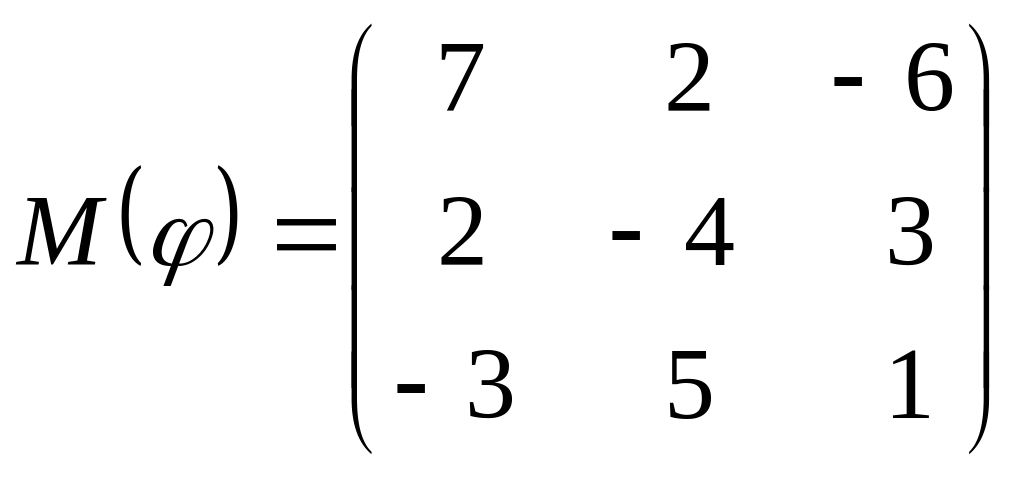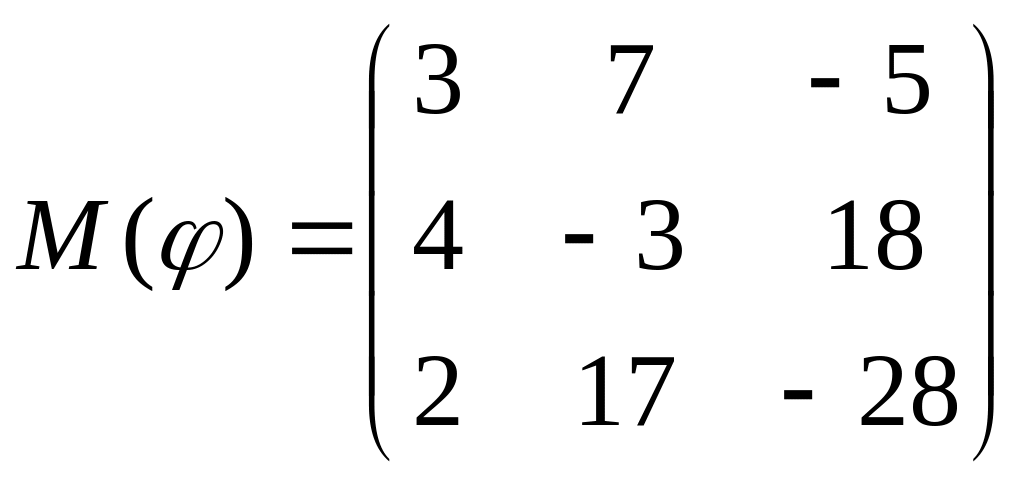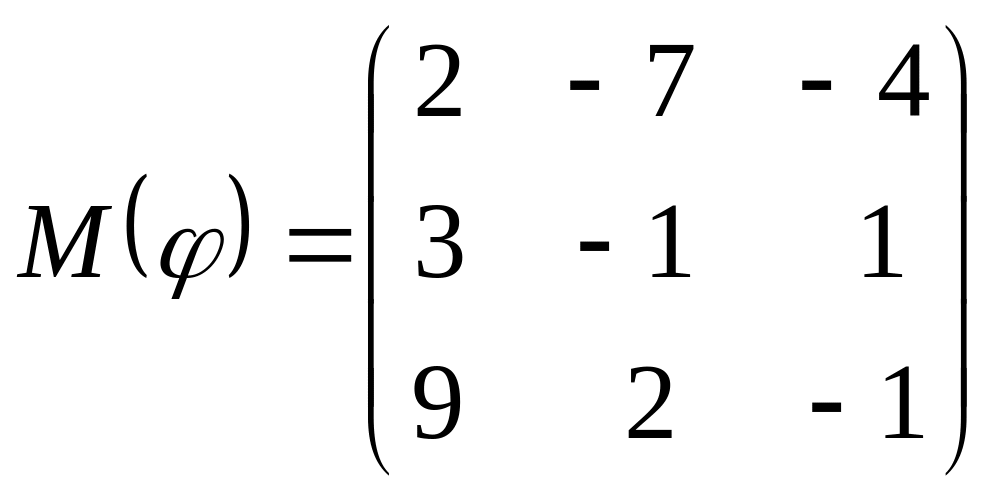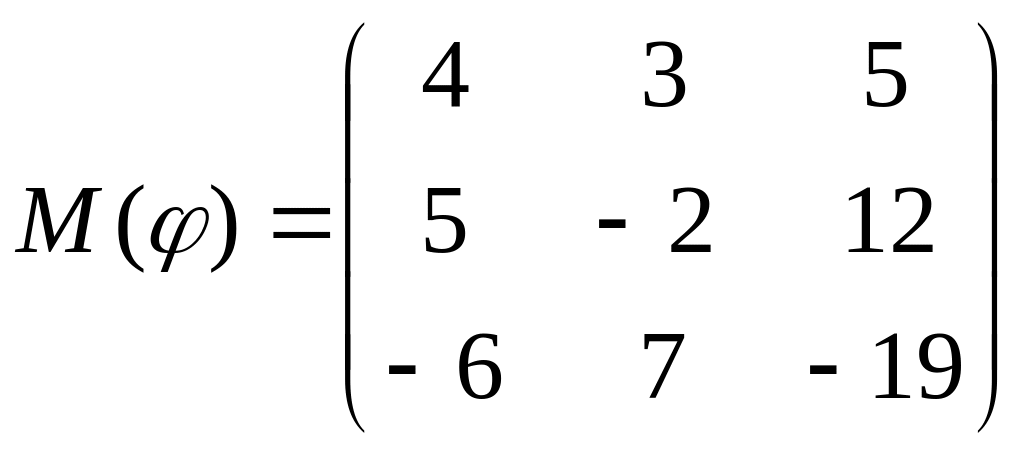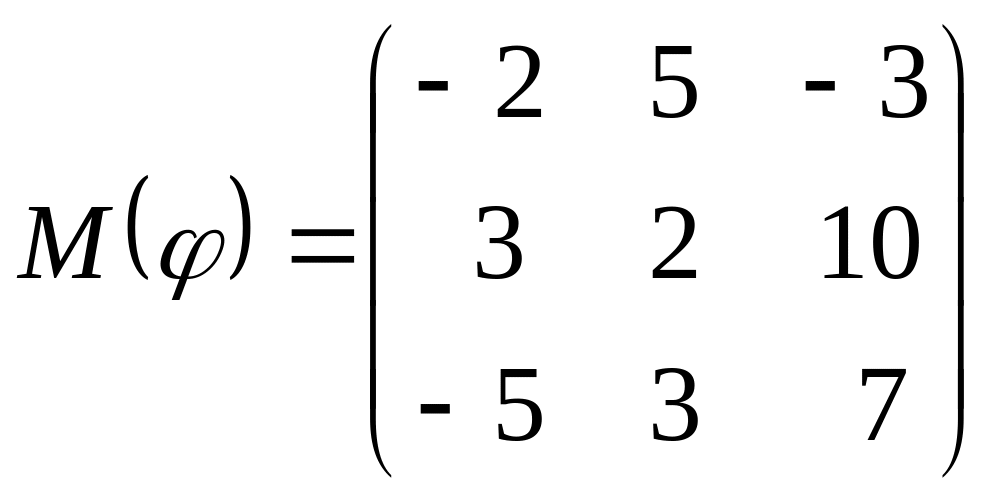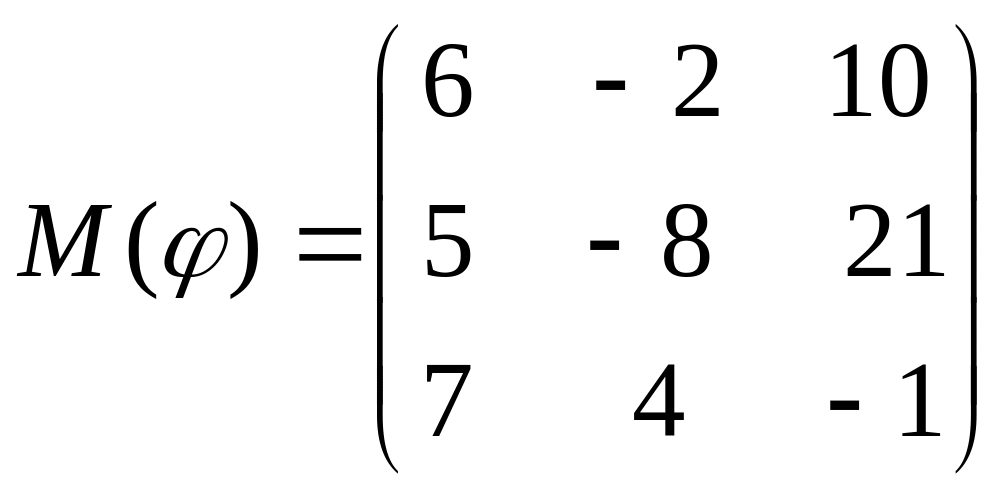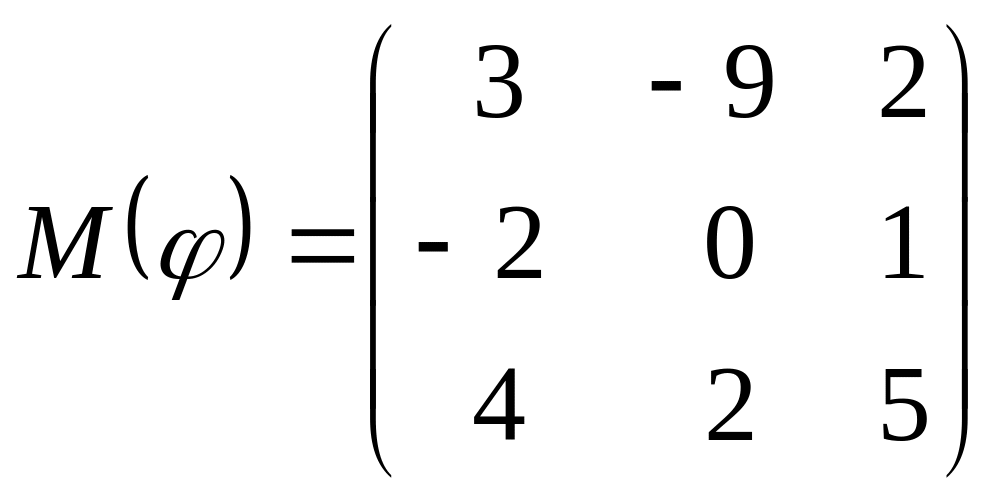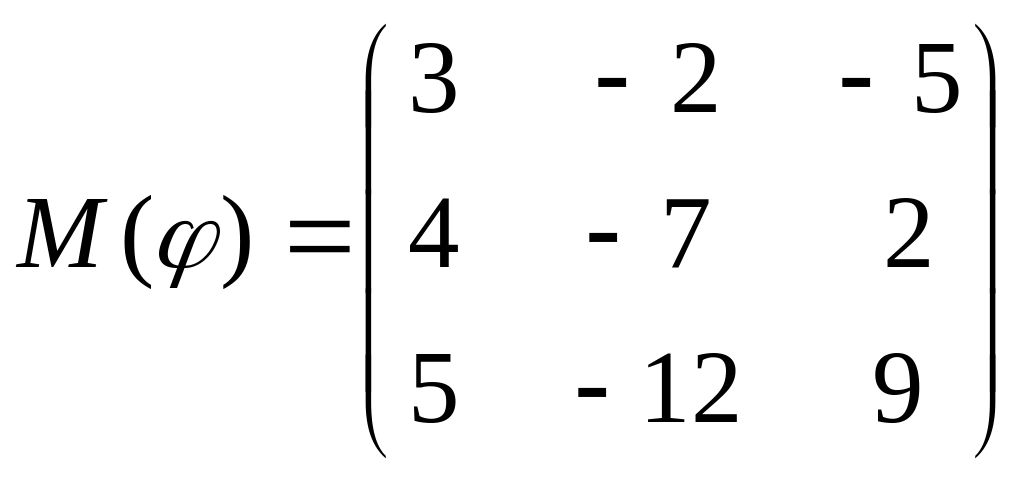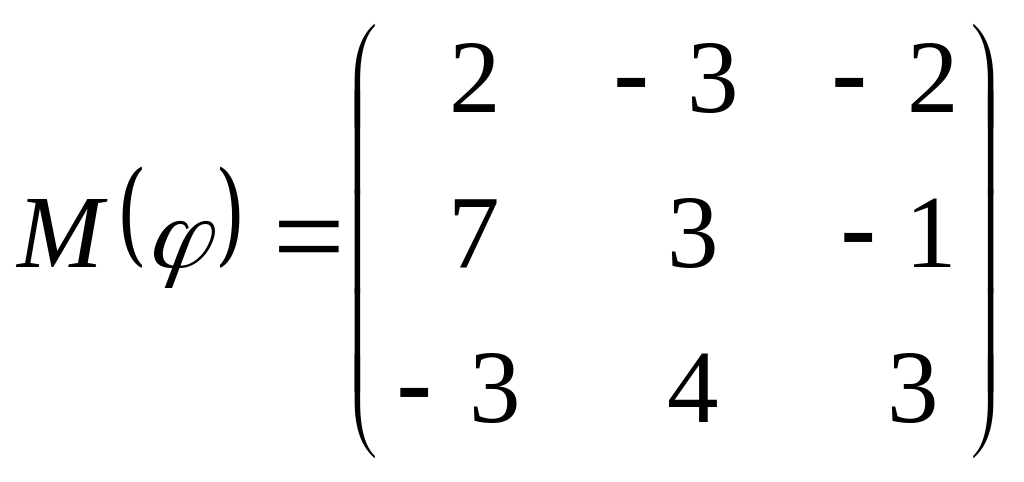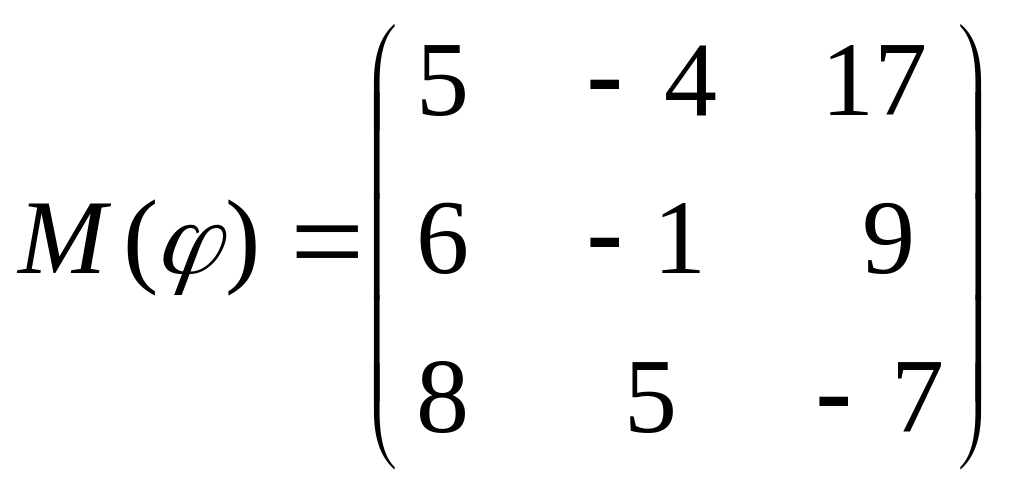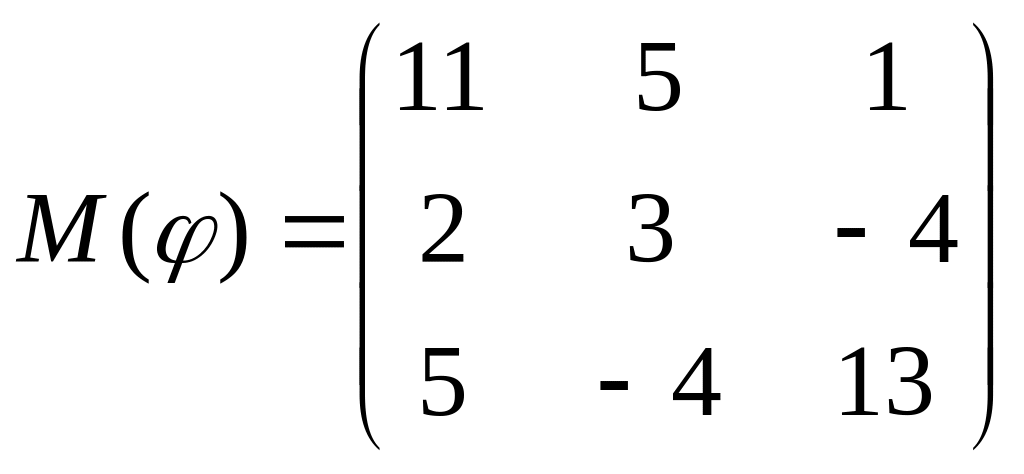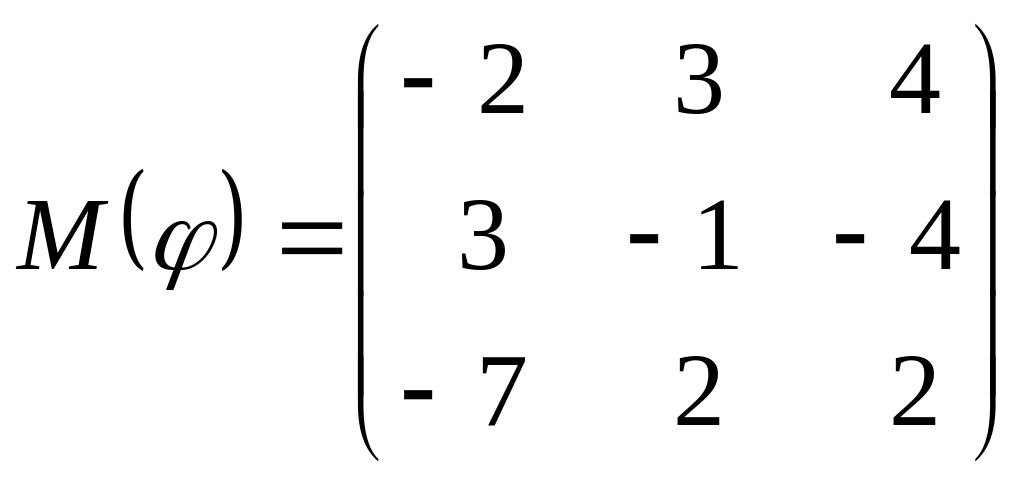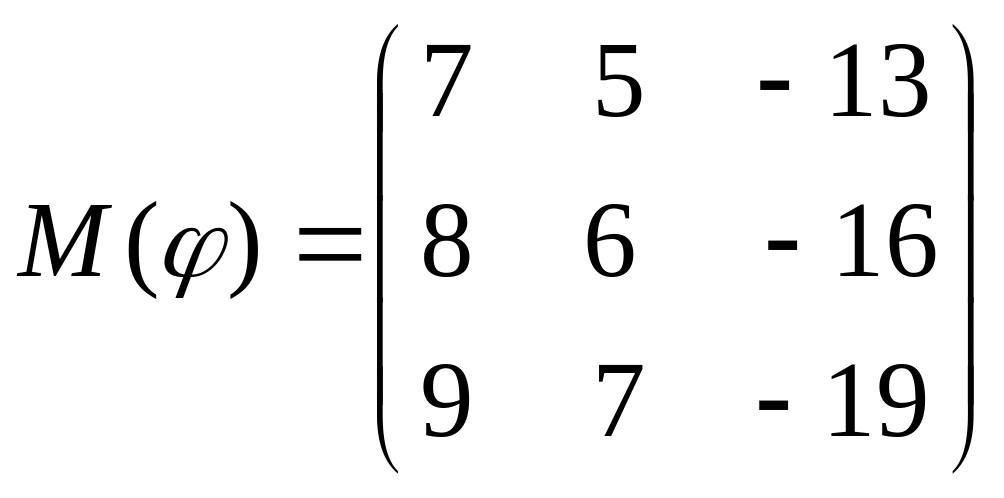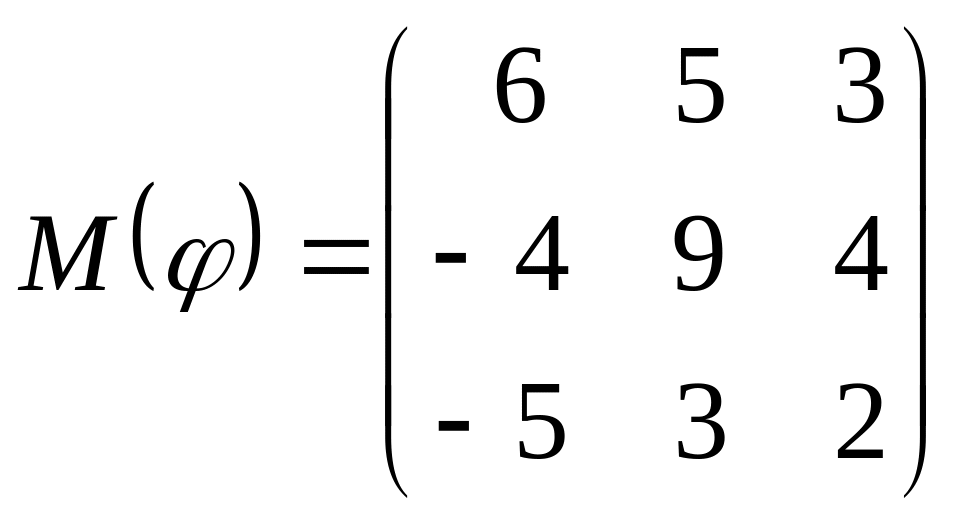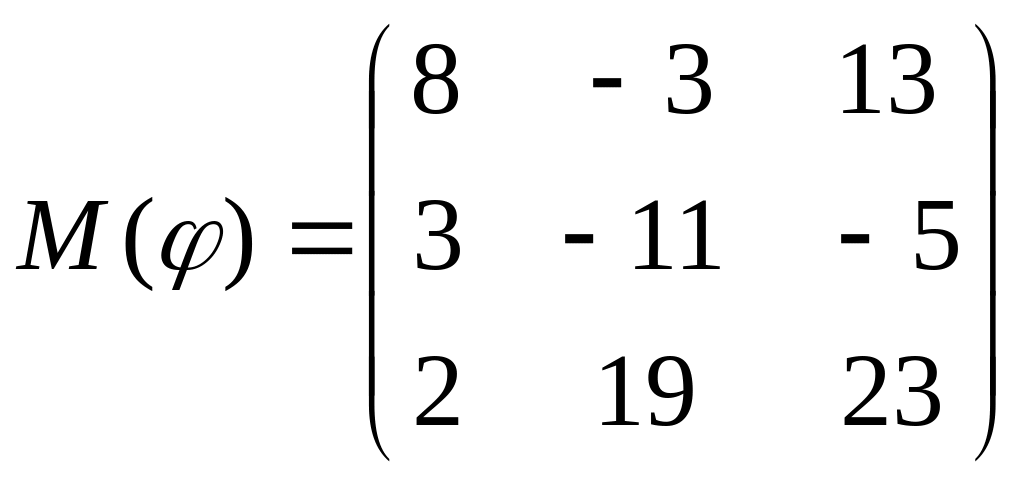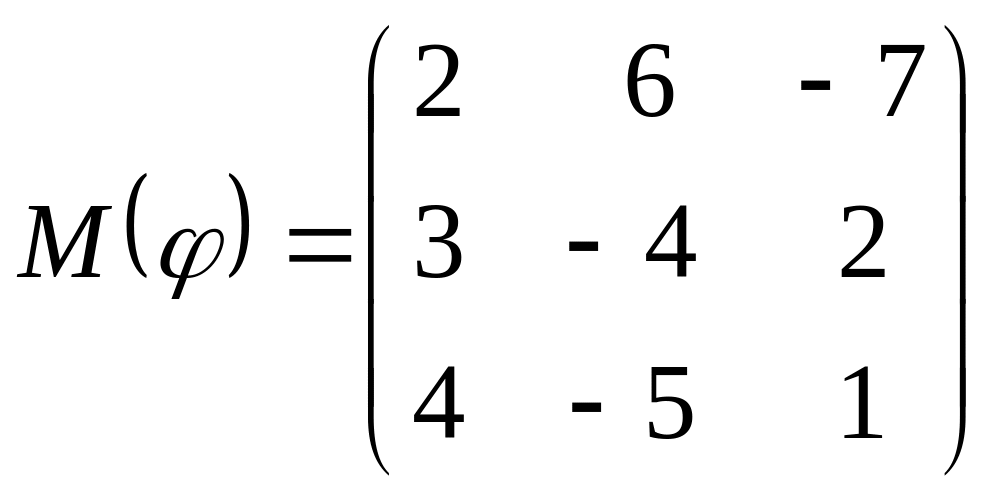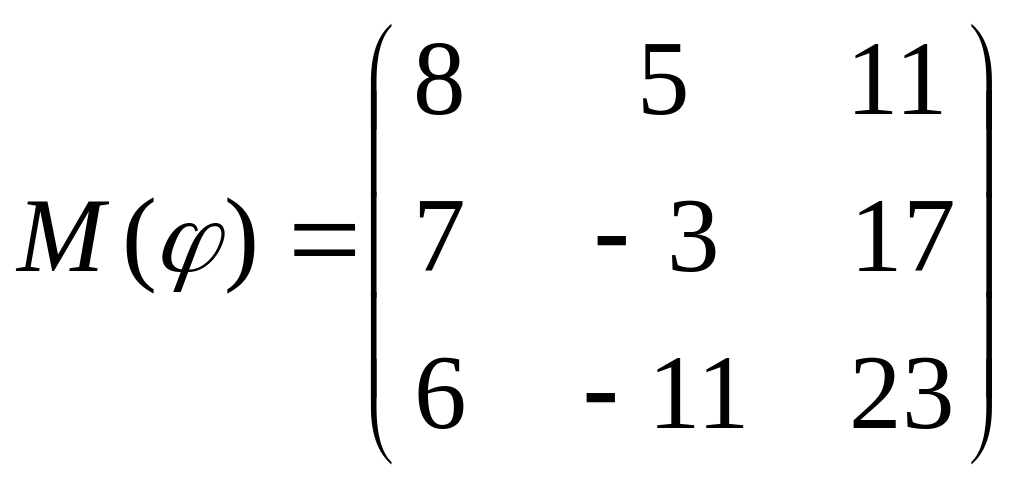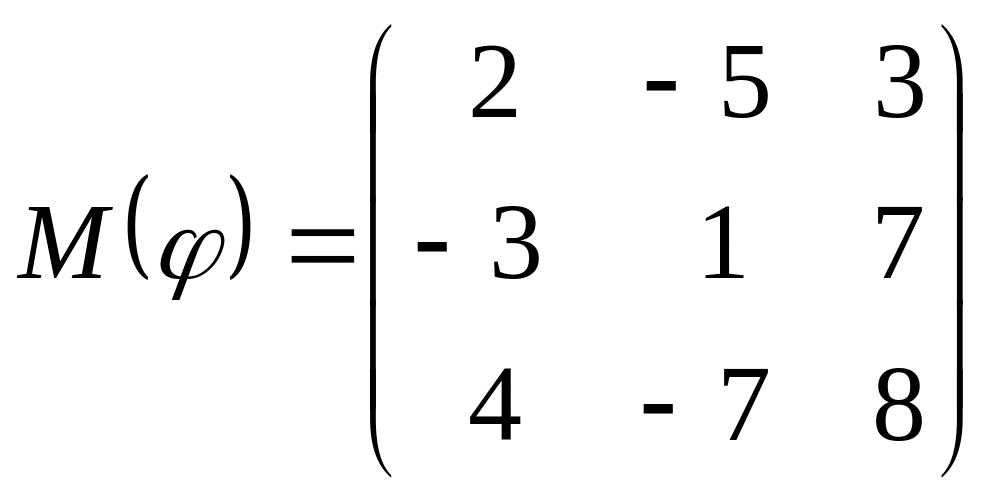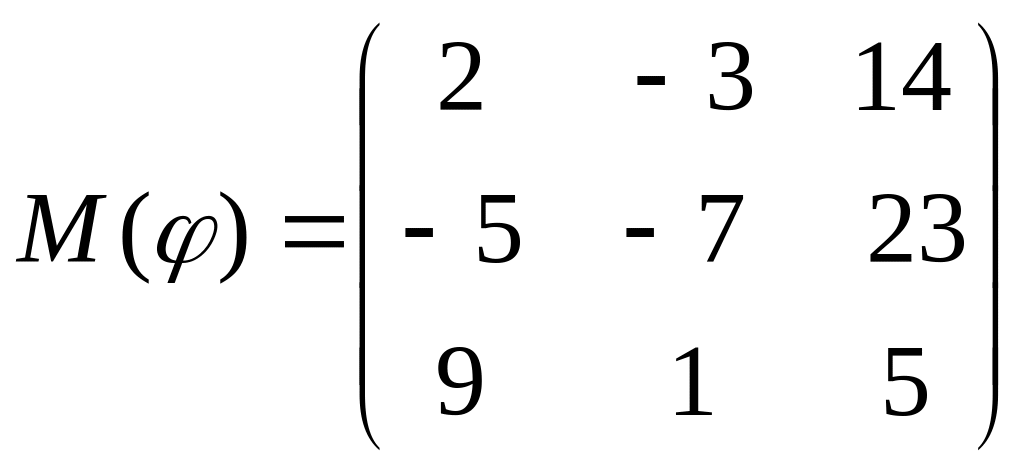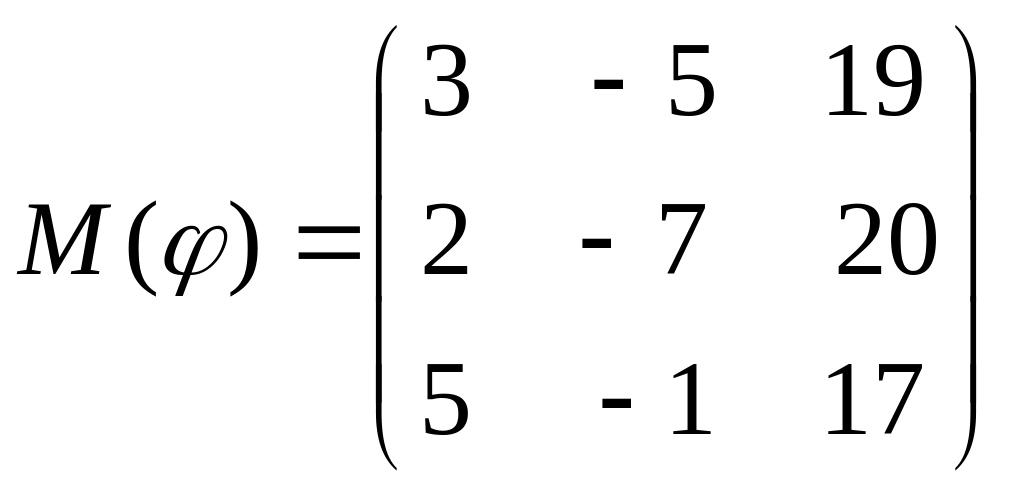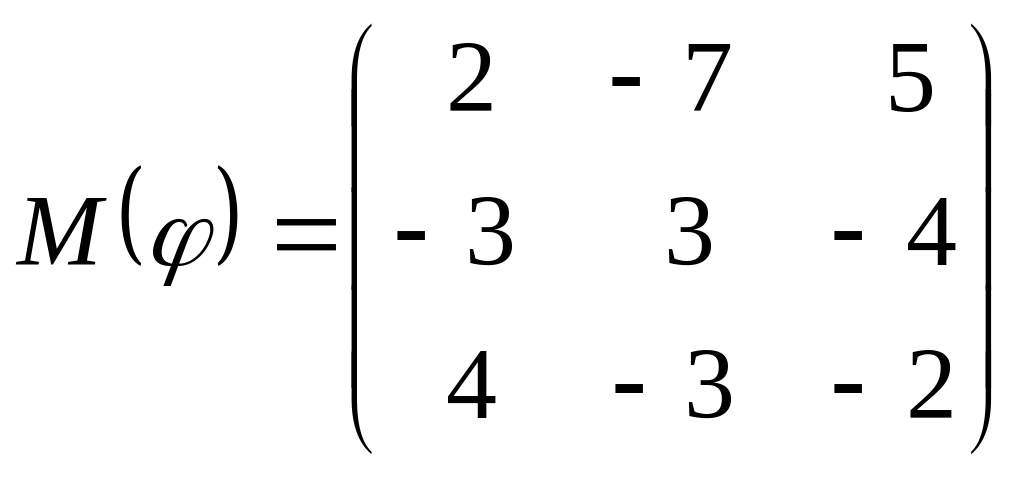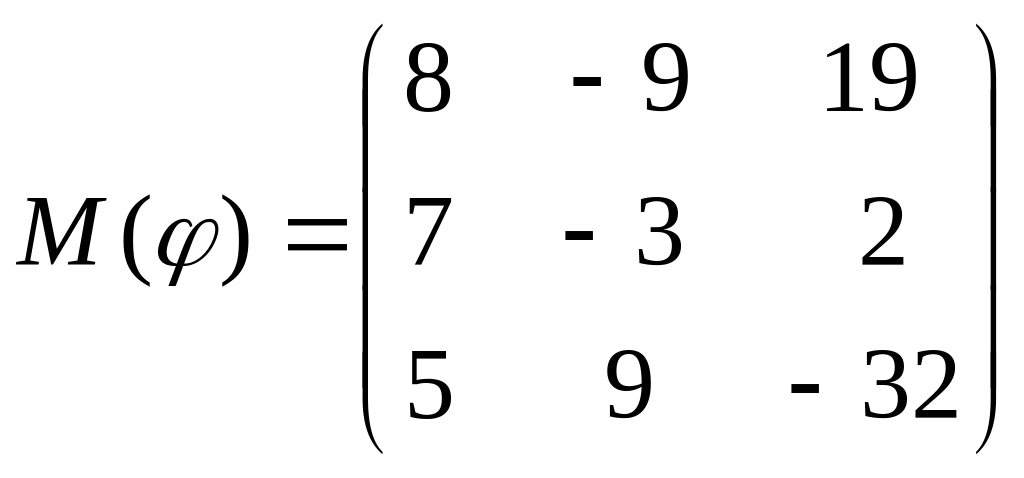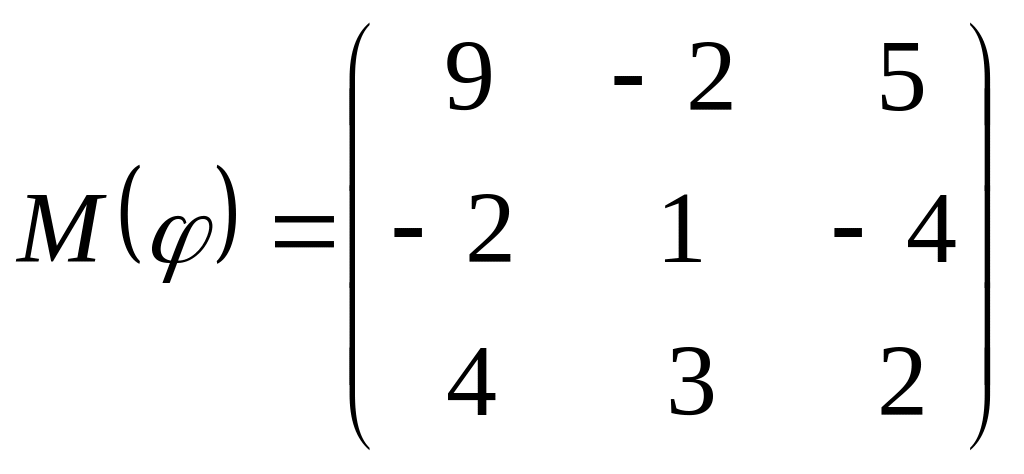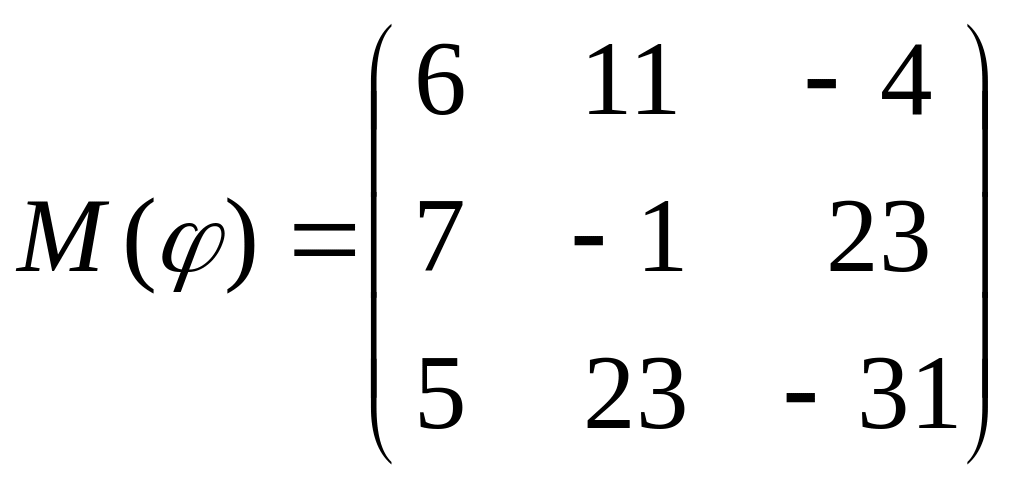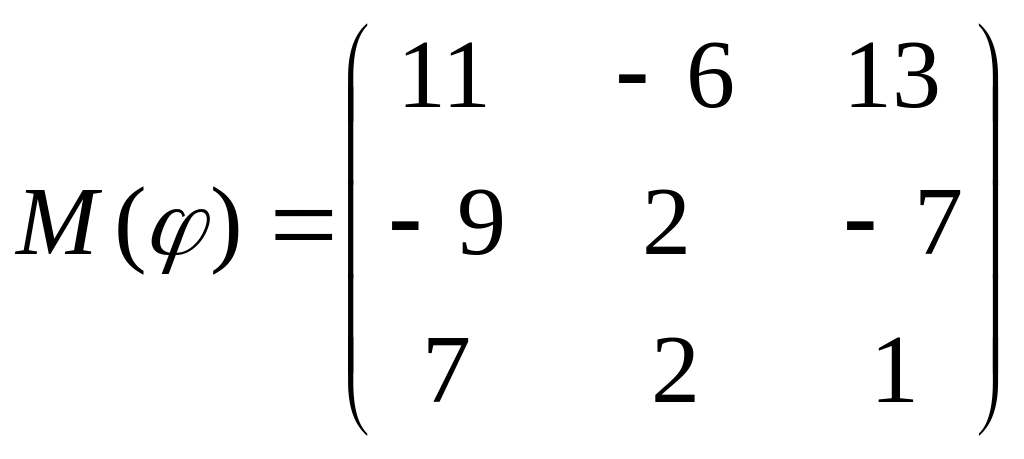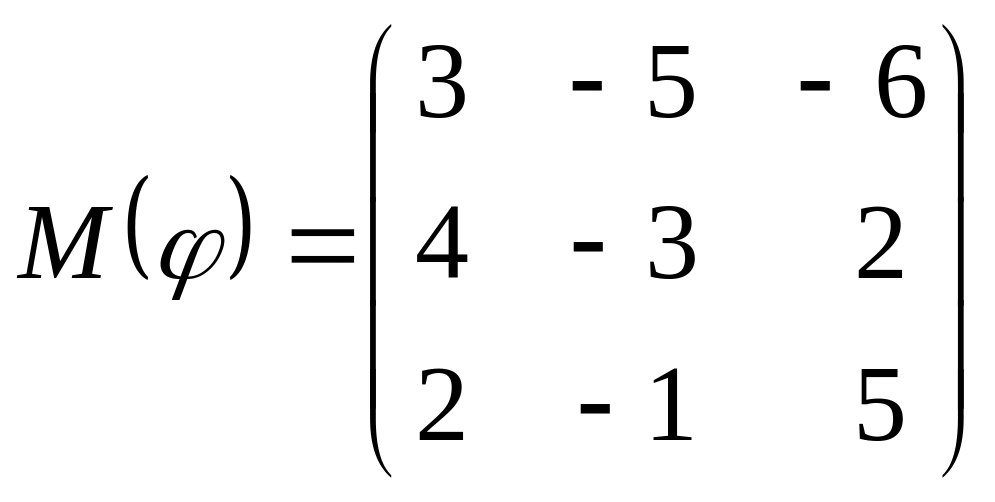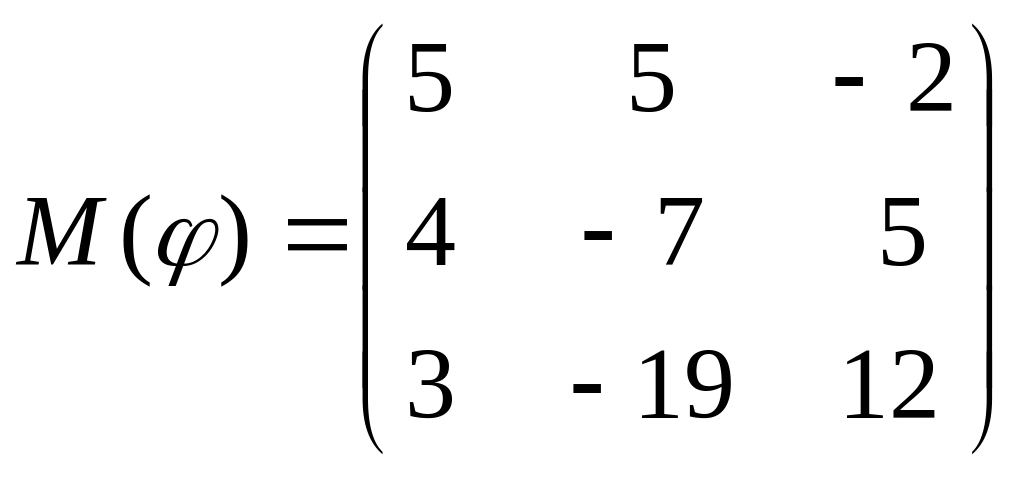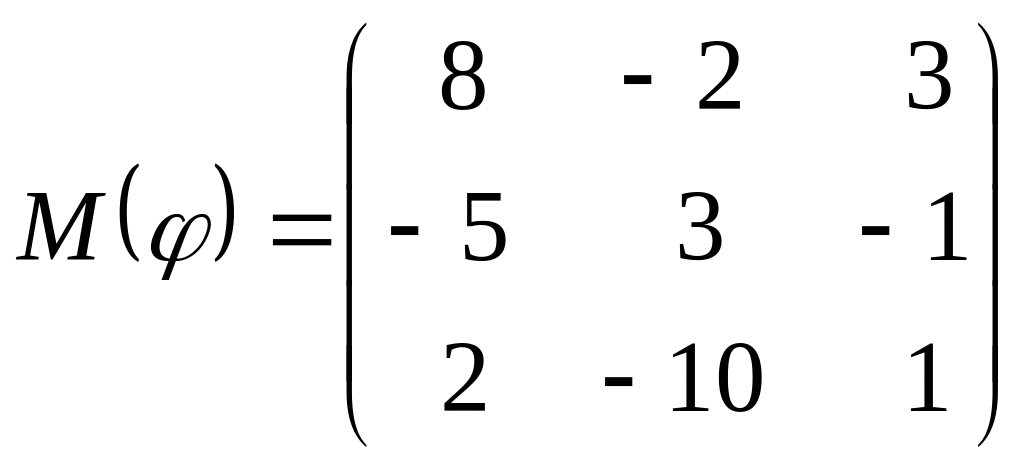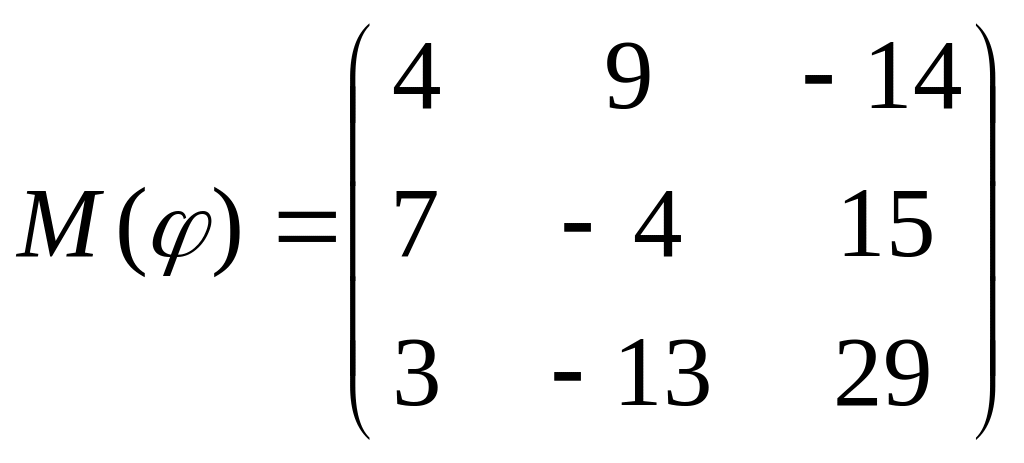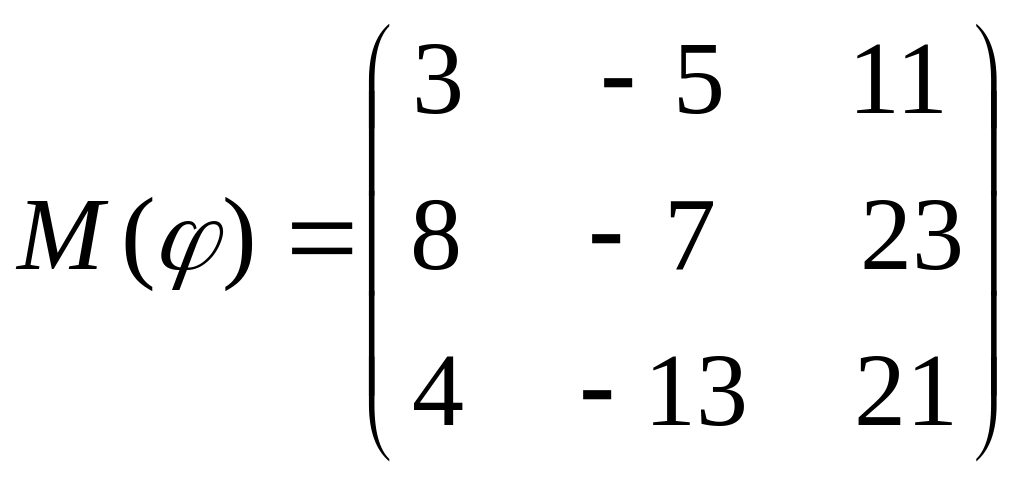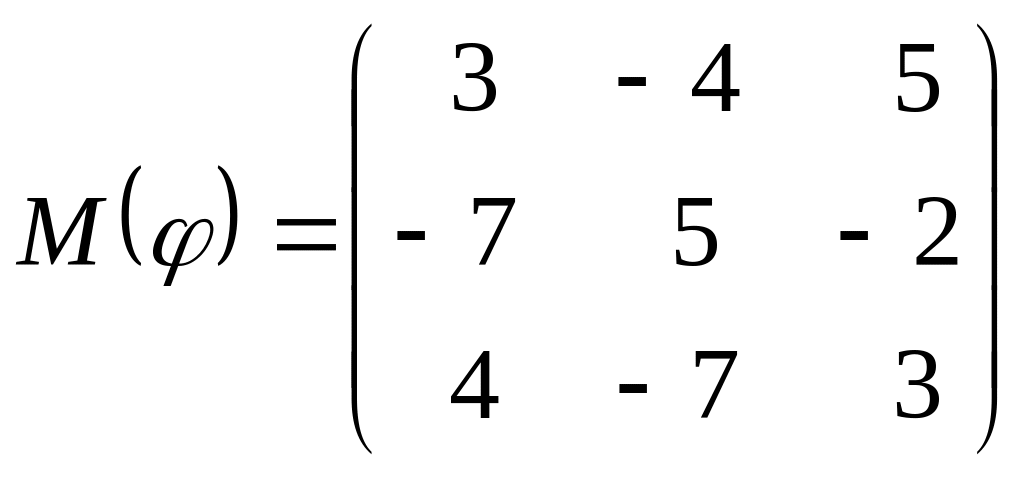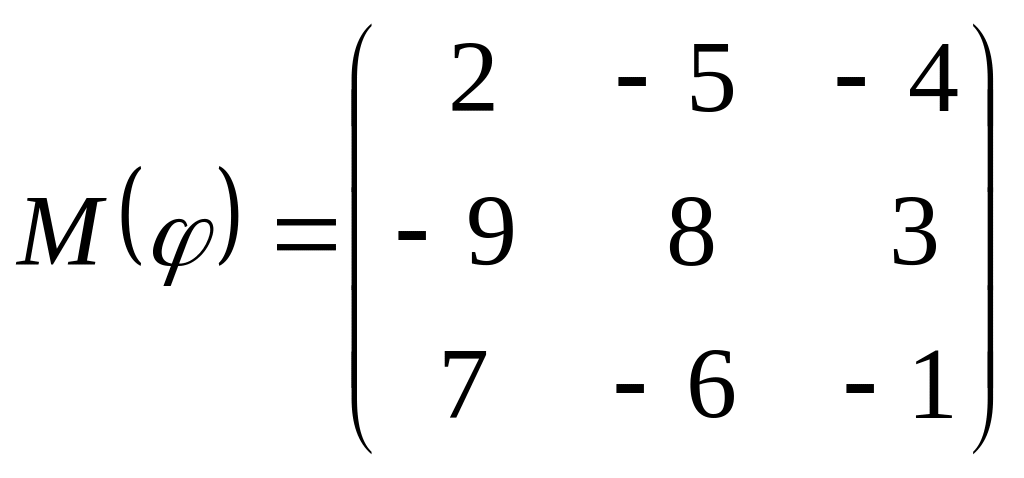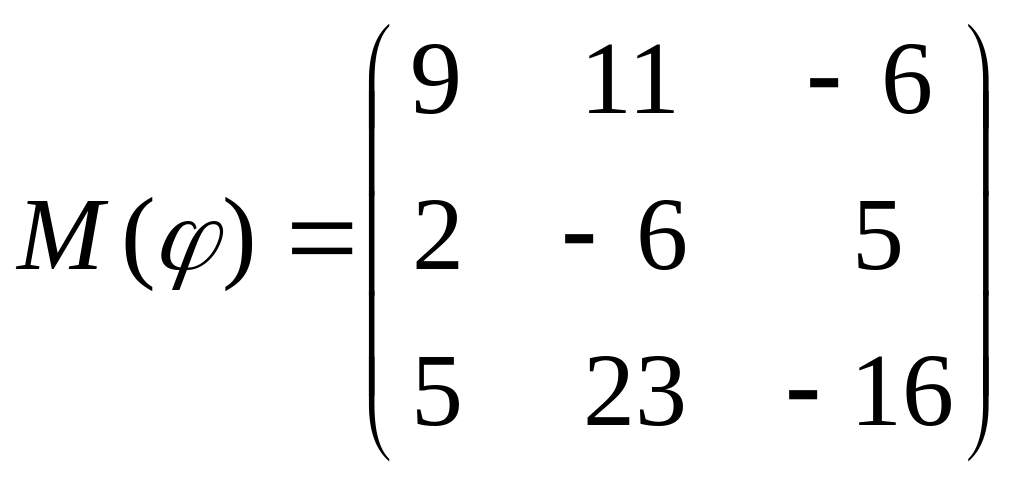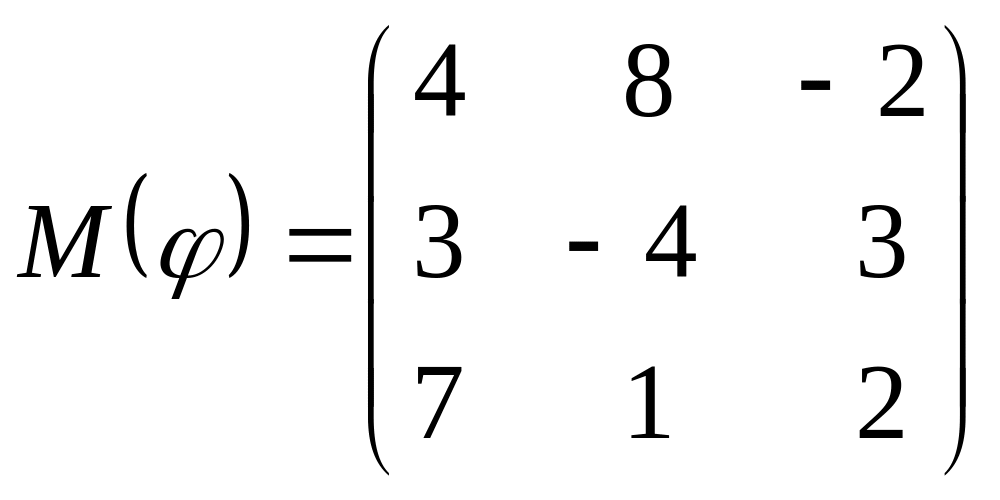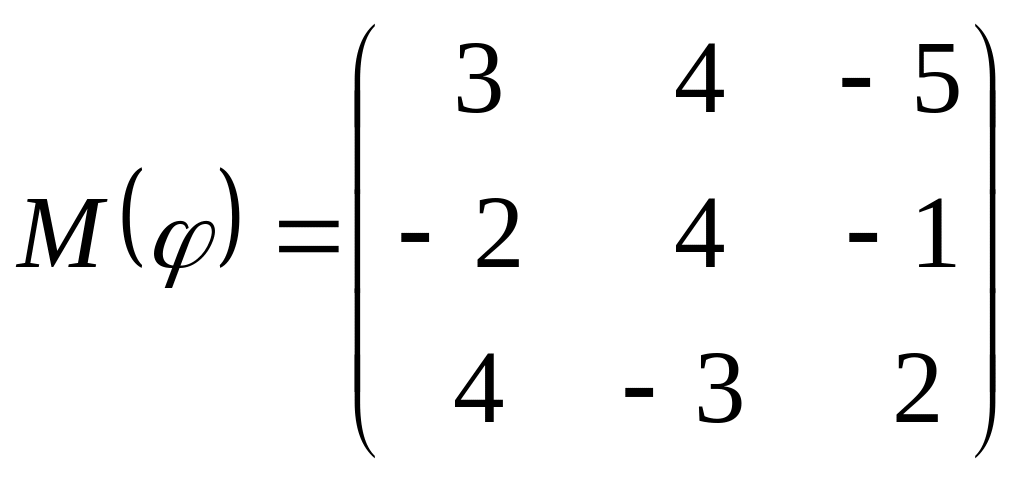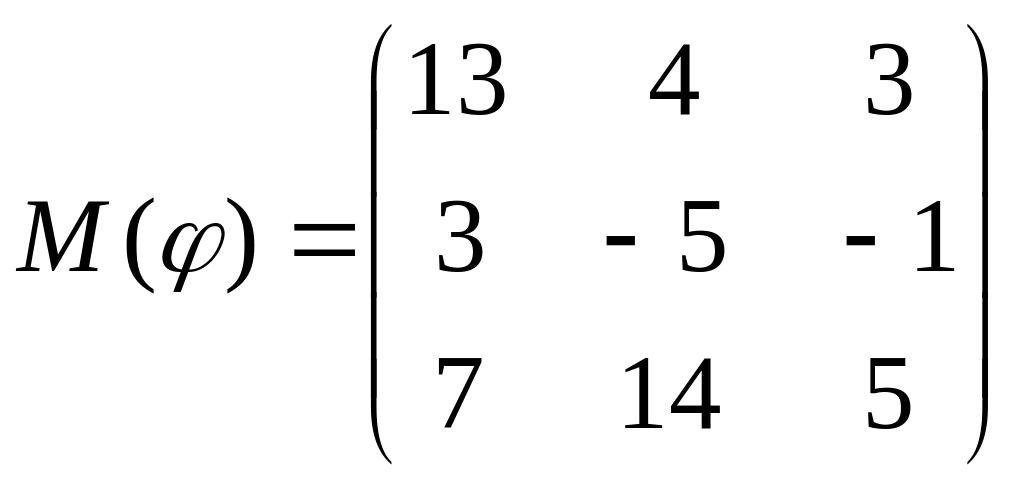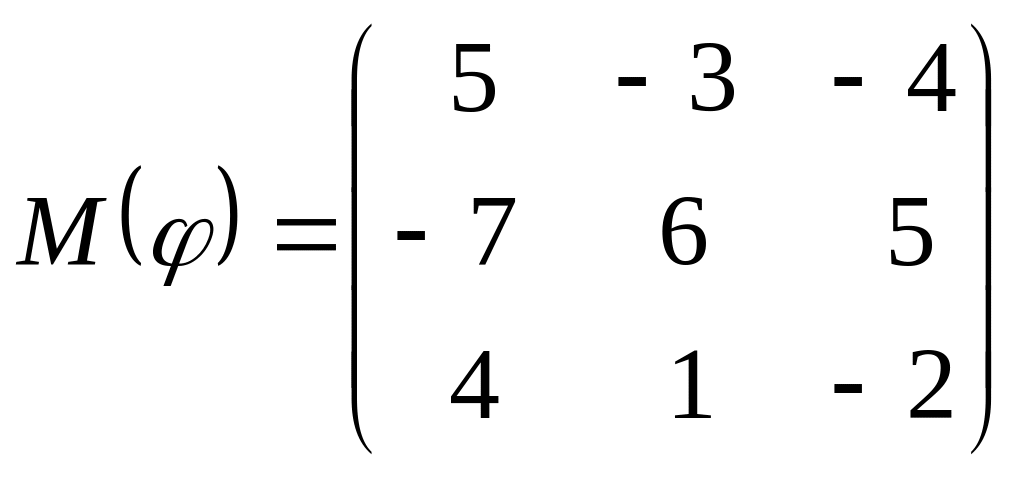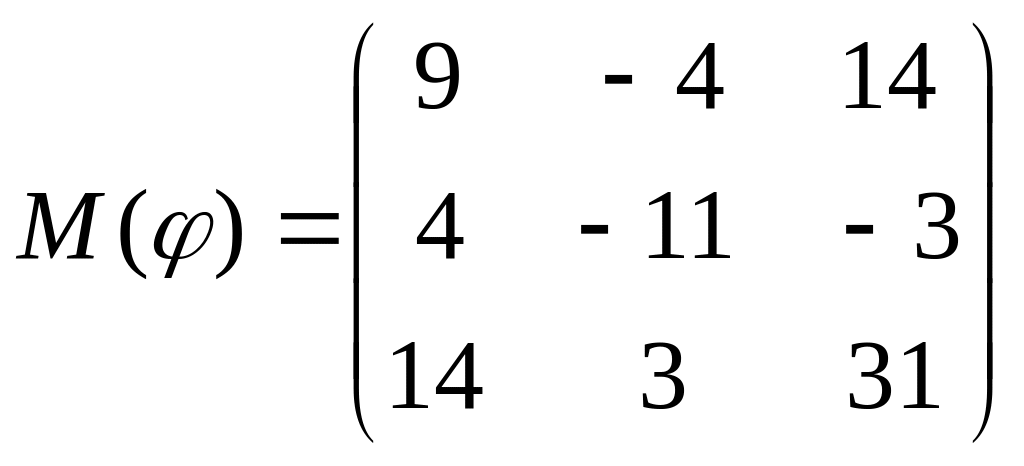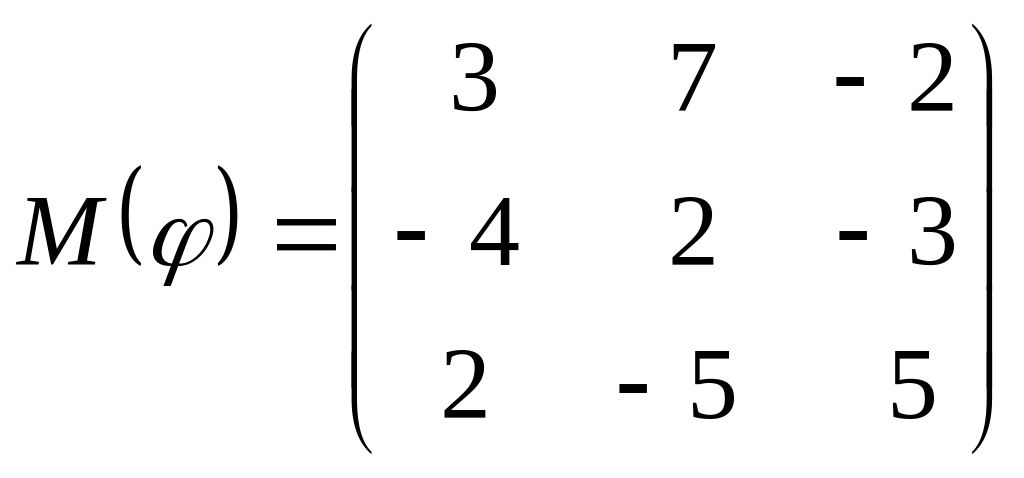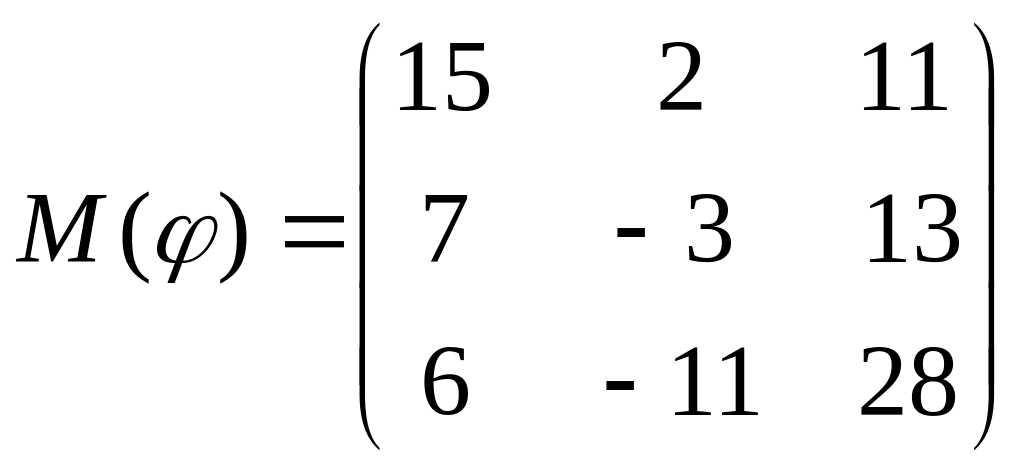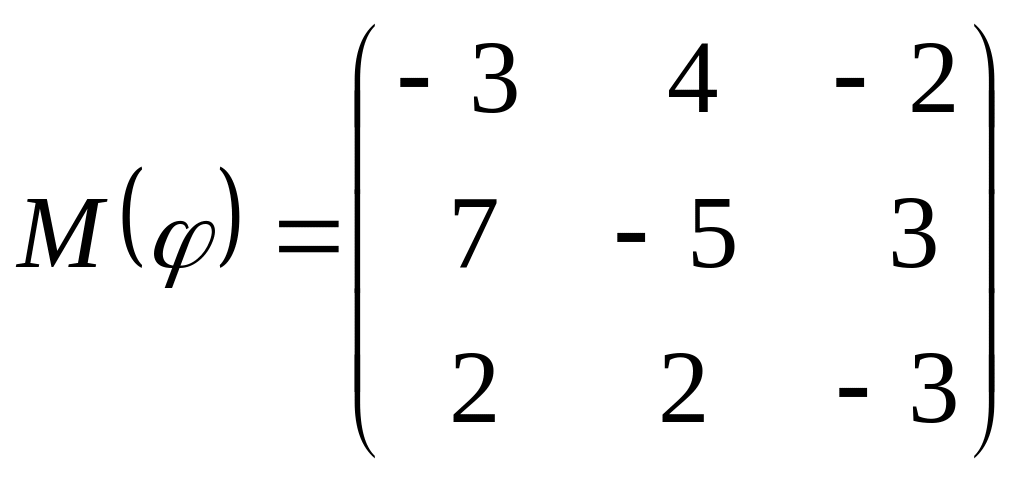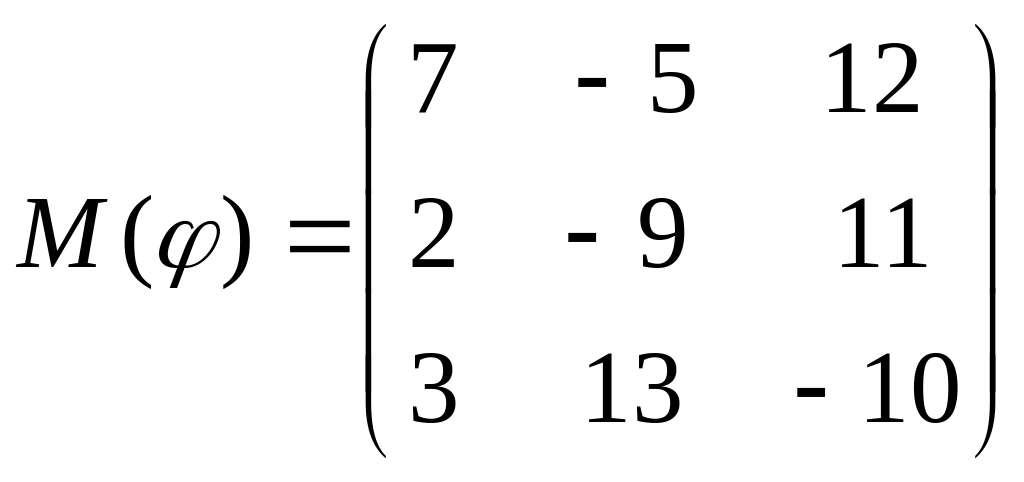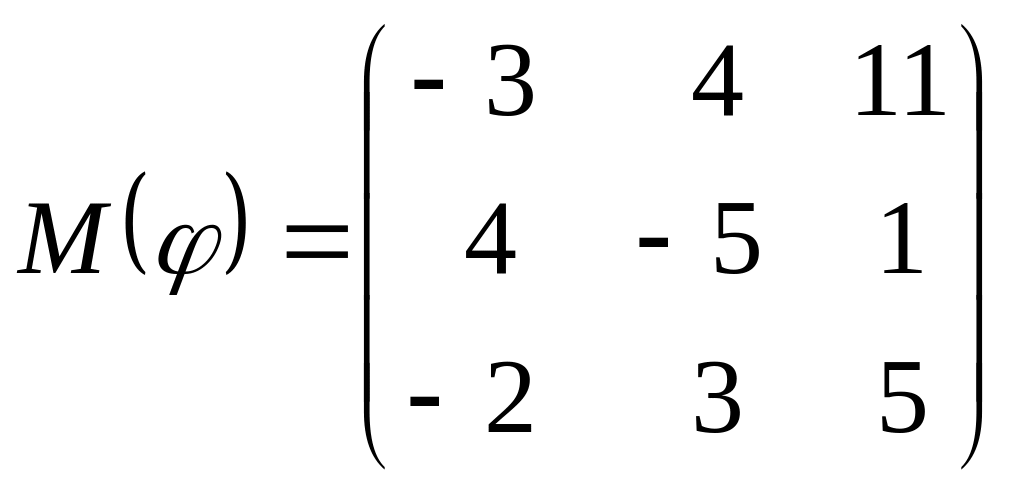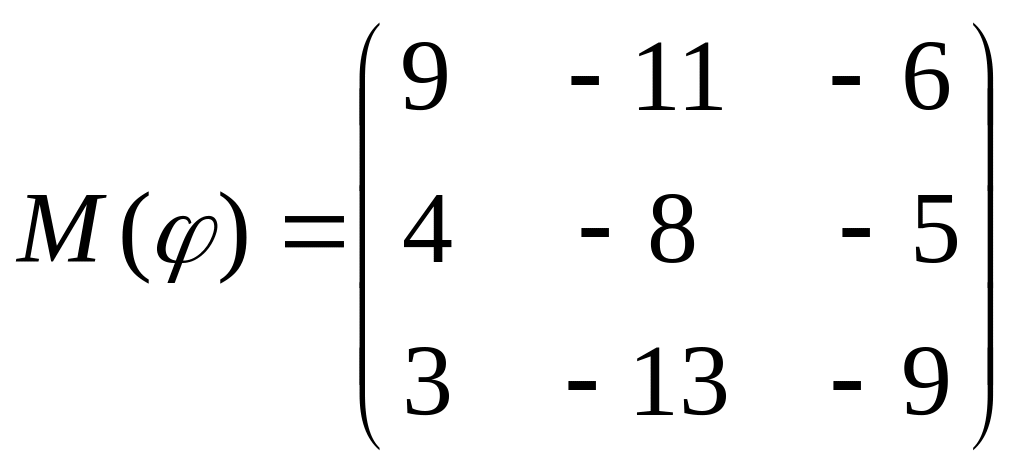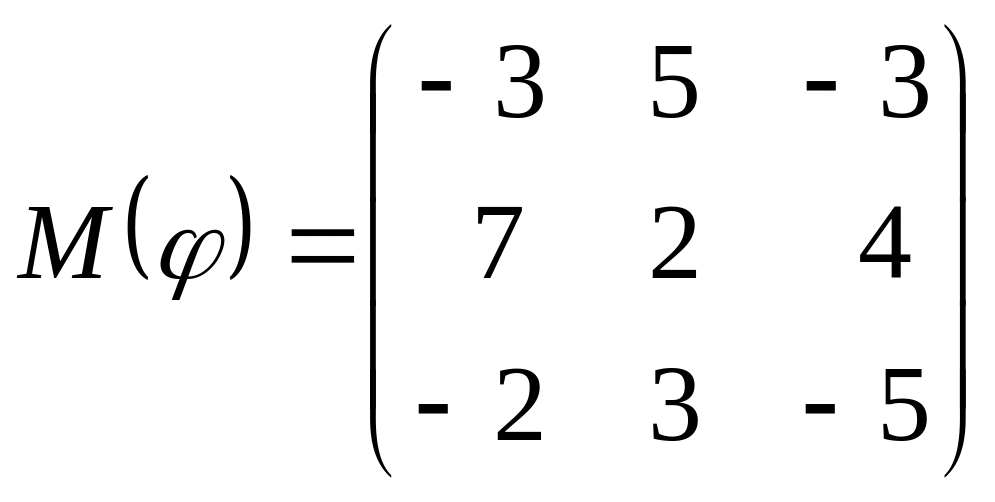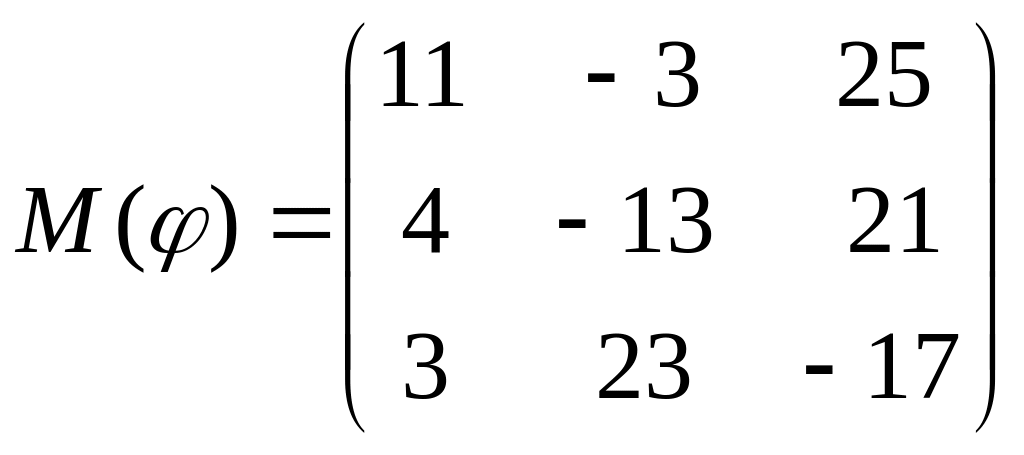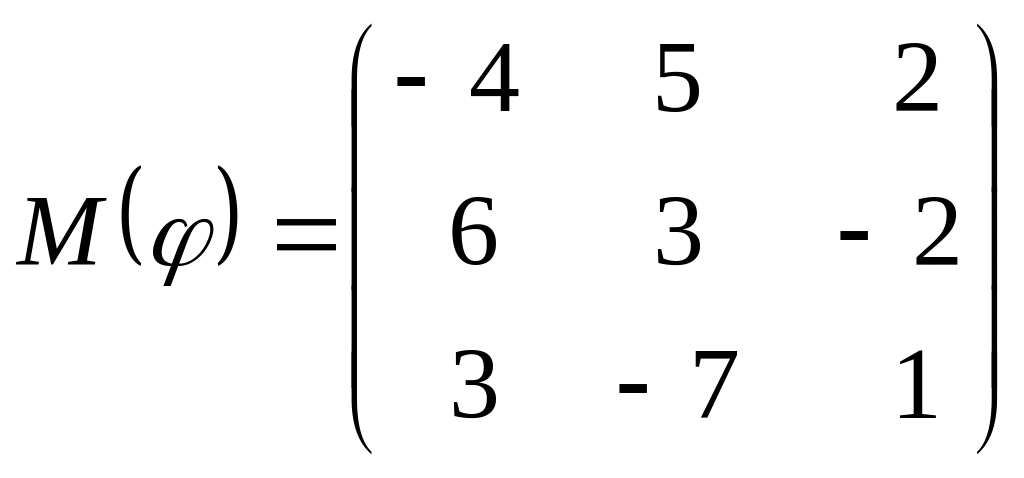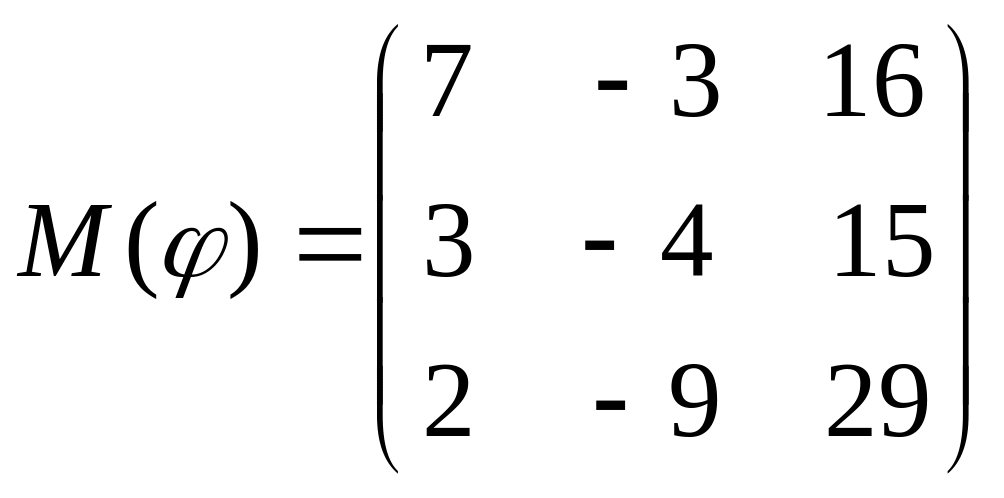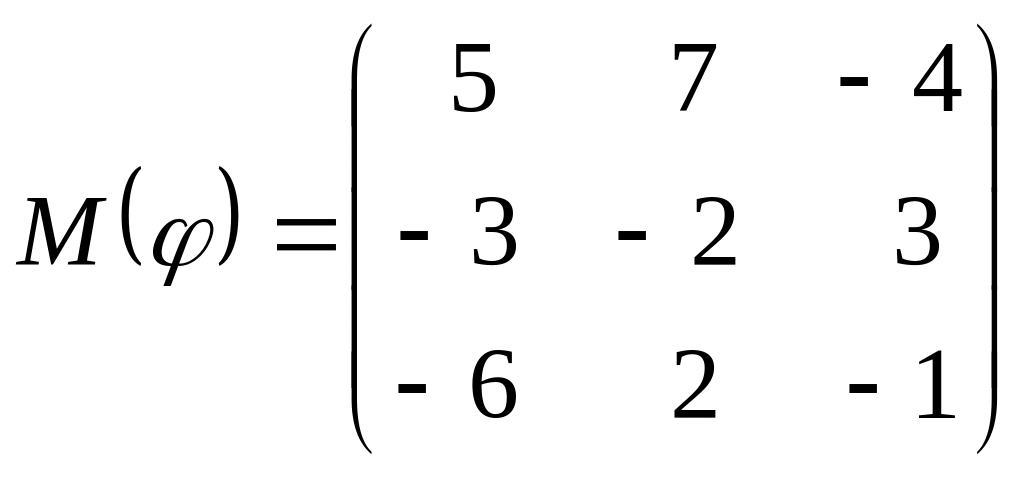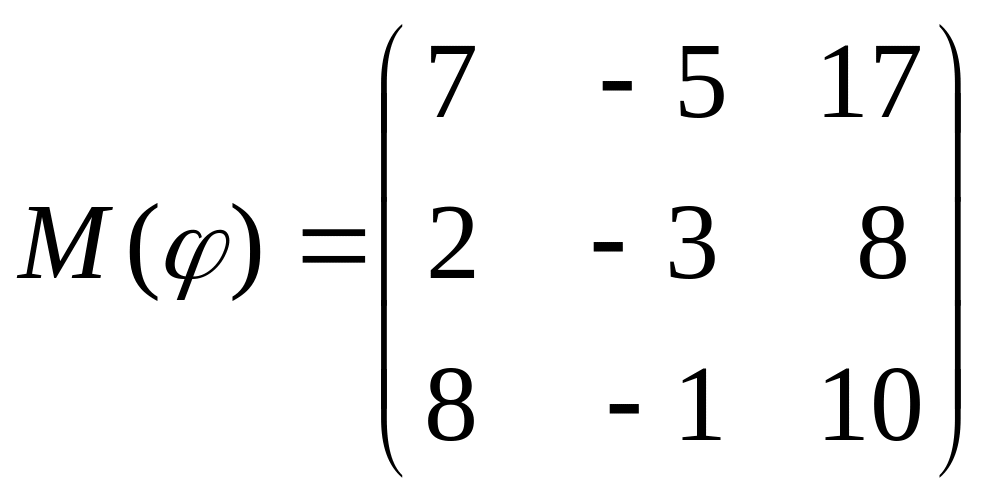6. Побудувати ортогональне доповнення підпростору до простору . Виконати перевірку. Яка розмірність ?
Вар. |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
31 |
|
32 |
|
33 |
|
34 |
|
35 |
|
36 |
|
37 |
|
38 |
|
39 |
|
40 |
|
41 |
|
42 |
|
43 |
|
44 |
|
45 |
|
46 |
|
47 |
|
48 |
|
49 |
|
50 |
|
7
а-в).
З’ясувати, чи є оператор φ
, заданий координатами, як функція
координат вектора
,
лінійним. У випадку лінійності знайти
його матрицю. Виконати перевірку. У
випадку нелінійності
проілюструвати на прикладі
невиконання
умов (умови) лінійного оператора.
Вар. |
7а |
7б |
7в |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
|
30 |
|
|
|
31 |
|
|
|
32 |
|
|
|
33 |
|
|
|
34 |
|
|
|
35 |
|
|
|
36 |
|
|
|
37 |
|
|
|
38 |
|
|
|
39 |
|
|
|
40 |
|
|
|
41 |
|
|
|
42 |
|
|
|
43 |
|
|
|
44 |
|
|
|
45 |
|
|
|
46 |
|
|
|
47 |
|
|
|
48 |
|
|
|
49 |
|
|
|
50 |
|
|
|
8 а-б). Лінійний оператор φ задано матрицею М(φ). Побудувати Ker φ та Іm φ, встановити їх розмірності. Чому дорівнює ранг і дефект лінійного оператора? Виконати перевірку.
Вар. |
8а |
8б |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|
|
31 |
|
|
32 |
|
|
33 |
|
|
34 |
|
|
35 |
|
|
36 |
|
|
37 |
|
|
38 |
|
|
39 |
|
|
40 |
|
|
41 |
|
|
42 |
|
|
43 |
|
|
44 |
|
|
45 |
|
|
46 |
|
|
47 |
|
|
48 |
|
|
49 |
|
|
50 |
|
|
9 а-б). Знайти власні вектори та власні значення лінійного оператора φ, заданого матрицею. Виконати перевірку.
10. Звести матрицю А до діагонального вигляду. Указати базис, в якому матриця А має діагональний вигляд.
Вар. |
9а |
9б |
10 |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
|
30 |
|
|
|
31 |
|
|
|
32 |
|
|
|
33 |
|
|
|
34 |
|
|
|
35 |
|
|
|
36 |
|
|
|
37 |
|
|
|
38 |
|
|
|
39 |
|
|
|
40 |
|
|
|
41 |
|
|
|
42 |
|
|
|
43 |
|
|
|
44 |
|
|
|
45 |
|
|
|
46 |
|
|
|
47 |
|
|
|
48 |
|
|
|
49 |
|
|
|
50 |
|
|
|
