Поверхностные интегралы I и II родов.
Пусть
-
ориентируемая кусочно - гладкая
поверхность,
и
-
скалярная и векторная функции, определённые
на
и непрерывные вдоль каж- дой из
поверхностей
.
Определение 1. Поверхностным интегралом первого рода от функции по кусочно-гладкой поверхности называют сумму поверхностных интегралов первого ро- да от по поверхностям .
Обозначают это понятие символом
.
Таким образом,
.
Определение 2. Поверхностным
интегралом второго рода от вектор-функции
по стороне
кусочно-гладкой поверхности
называют сумму поверхностных интегралов
второго рода от
по
.
Обозначают это понятие символом
Σ
. Таким образом,
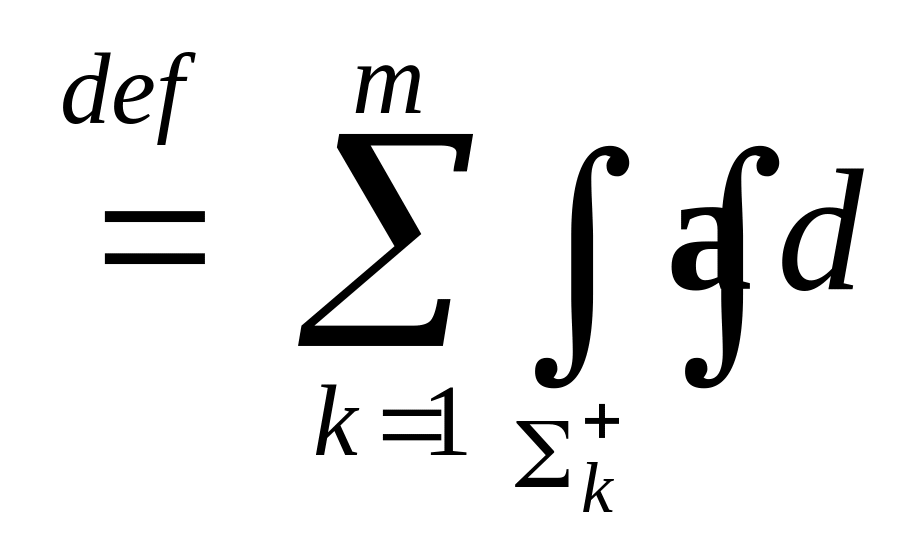Σ
Σ
2.3. Формулы Стокса и Остроградского –Гаусса..
Пусть функции и непрерывны и имеют непрерывные частные производные первого порядка по каждому из своих аргументов в некоторой об- ласти . Обозначим: ;
;
Пусть
-
ориентируемая кусочно - гладкая
поверхность, содержащаяся в области
,
а простой и кусочно- гладкий контур
- край этой поверхности. Пусть
-
одна из сторон поверхности
,
а
-
одна из ориентаций её края. Будем
говорить, что сторона
и
ориентация края
согласованы, если наблюдатель,
идущий по стороне
вдоль края
,
оставляет поверхность слева от себя.
Теорема. (Стокс) Пусть вектор-функция и кусочно-гладкая поверх- ность удовлетворяют указанным выше условиям. Тогда dΣ , где - одна из сторон поверхности , а Г - край , ориентация которого согласована со сторо- ной .
► Пусть
-
ориентируемая кусочно - гладкая
поверхность,
-
согласованная ориентация краёв, а
-
сторона поверхности
,
согласованная с ориен- тацией
её
края; здесь
.
По формуле Стокса для поверхности
простой отно- сительно координатной
оси ( п. 1.4.)
dΣ
,
.
Сложив эти равен- ства почленно, получим:
Σ.
Сумма в правой части этого равенства
равна, очевидно,
dΣ
. Пусть
- дуга, общая для каких –то двух контуров
и
набора
(
следовательно,
не является частью края Г поверхности
)..
Ори- ентация, полученная
от
,
противоположна ориентации, полученной
ею от
.
При составлении суммы
интегрирование
по
производится дважды, причём в
противоположных направлениях, а такие
интегралы аннулируют друг друга. Значит,
в сумме
будут аннулированы все интегралы по
дугам, не принадлежащим краю Г;
поэтому
.
◄
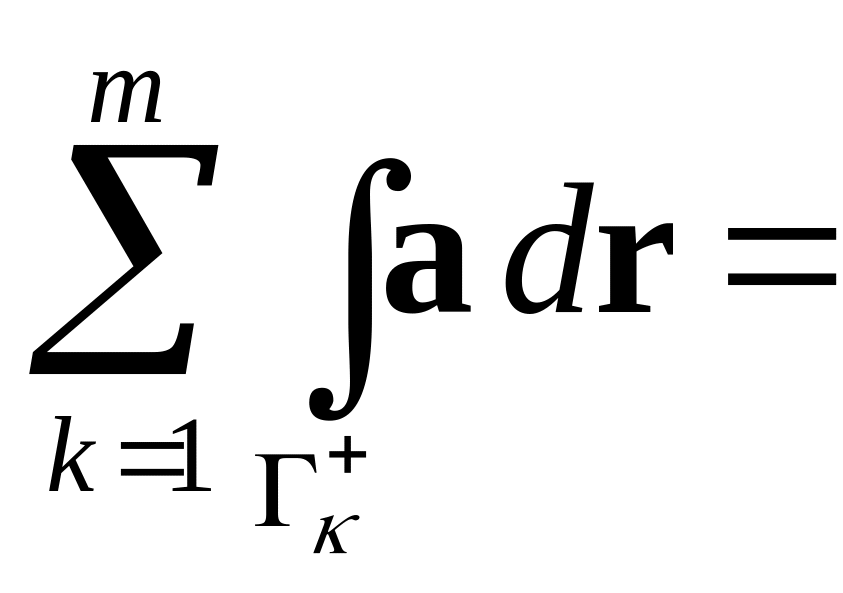
Пусть
-
ограниченная область, граница которой
представляет собой кусочно- - гладкую
замкнутую поверхность
.
Будем различать две стороны такой
поверхности – внутреннюю
и внешнюю
-
в соответствии с направлением орта
нормали.
Теорема ( Остроградский, Гаусс)
Пусть
-
ограниченная область, граница ко- торой
представляет собой кусочно - гладкую
замкнутую поверхность
.
Пусть функция
и
,
а также их производные
и
непрерывны на
.
Тогда
.
► Доказательство этого равенства
приведём для частного случая: будем
считать, что множество
является простым относительно каждой
из координатных осей. Таким свойством
обладают, например, шар, эллипсоид,
параллелепипед. В указанных условиях
докажем три равенства:
*)
,
**)
;
***)
.
Докажем равенство ***), пользуясь простотой множества относительно оси :
.
Здесь
-
проекция точки Р (х,у,z)
на плоскость
,
В – проекция множества X.
В представляет собой плоскую
область, границей которой является
простой кусочно-глад- кий контур
.
Функции
и
непрерывно дифференцируемы в В. Внешняя
сторона
поверхности
,
ограничивающей X,
состоит из трех компонент:
.
Здесь
- нижняя сторона поверхности
,
уравнение которой
,
-
верхняя сторона поверхности
,
уравнение которой
,
а
-
внешняя сторона цилиндрической
поверхности, образующие которой
параллельны оси
,
направляющей является контур
(впрочем, эта компонента может
отсутствовать, как, например, в случае,
когда Х есть шар). Таким образом,
.
есть поверхностный интеграл от
вектор-функции
,
где
,
а
.
Вектор а параллелен оси
.
Значит, его проекция на нор- маль к
цилиндрической поверхности
равна нулю; поэтому
=
0.Следо- вательно, в любом случае ( имеется
компонента
или её нет) имеем( см. п. 1.3. , форму- ла I):
=
=
.
С другой
стороны,
=
.
Таким образом,
равенство ***) справедливо. Доказательства
равенств **) и *) аналогич- ны. В доказательстве
равенства **) следует опираться на
простоту множества Х относи- тельно
оси
:
,
в доказательстве равенства *) – на простоту множества Х относительно оси :
.
◄