1. Понятие кривой. Параметризация кривой

Определение. Элементарной кривой называется образ открытого отрезка при топологическом отображении его в пространство.

Уравнения

(1.1)

называются параметрическими уравнениями кривой , кривая — параметризованной кривой, гомеоморфизм , порождающий кривую, — параметризацией кривой.

векторное уравнение кривой :

(1.2)

Определение. Множество называется простой кривой, если это множество связно и у каждой его точки есть такая окрестность , что является элементарной кривой.

Простая кривая гомеоморфна или открытому отрезку или окружности.

Определение. Множество точек пространства будем называть общей кривой (в дальнейшем — просто кривой), если это множество является образом простой кривой при локально топологическом отображении ее в пространство.

2. Различные уравнения кривой

Определение. Простая кривая называется регулярной кривой класса (k раз дифференцируемой), если у каждой точки этой кривой есть окрестность, которую можно задать параметрическими уравнениями

)

где , , — раз непрерывно дифференцируемые функции.

Рассмотрим различные аналитические способы задания кривой.

Теорема 1. Если , и — раз непрерывно дифференцируемые функции, удовлетворяющие условию

то система равенств (1) является уравнениями некоторой кривой . Эта кривая есть образ отрезка при локально топологическом отображении, которое точке отрезка ставит в соответствие точку кривой.

Определение. Кривая, заданная уравнениями (1), называется кусочно-регулярной, если промежуток, на котором она определена, можно покрыть не более как счетным множеством промежутков, внутри каждого из которых уравнения (1) определяют регулярную линию (на концах промежутков требование регулярности может нарушаться).

Уравнения (5) называют явными уравнениями кривой.

Теорема 2. Пусть регулярная кривая в некоторой окрестности точки , соответствующей параметру , имеет уравнения (1), при этом . Тогда в достаточно малой окрестности точки кривая может быть задана уравнениями (5), где и — раз непрерывно дифференцируемые функции.

Неявное задание кривой уравнениями

Если в точке не равен 0 определитель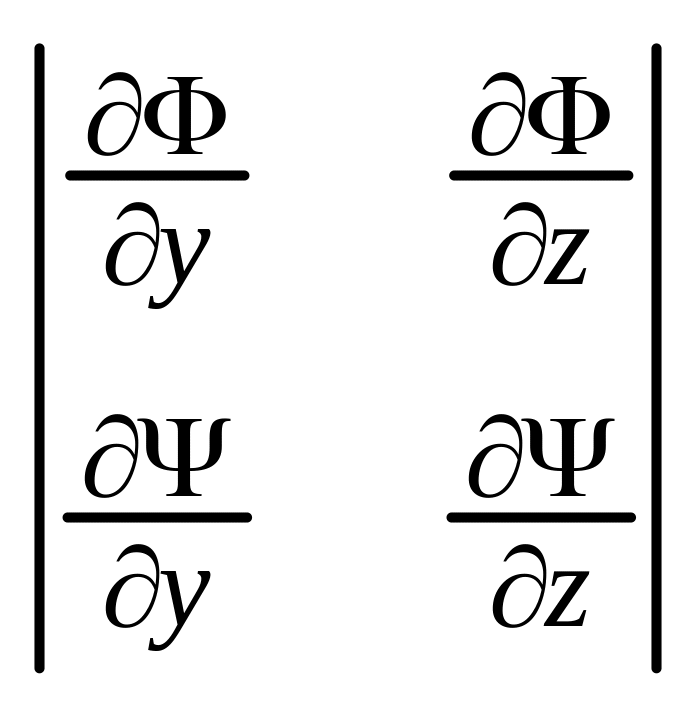 ,то в окрестности систему уравнений (6) можно разрешить относительно и . Получим , .

2. Естественная параметризация кривой. Длина дуги

1. Длина дуги. Пусть — регулярная кривая, заданная уравнениями

где , , — раз непрерывно дифференцируемые функции и их производные , , одновременно не обращаются в нуль на всем промежутке . От параметрического задания кривой (1) перейдем к векторному

в котором векторная функция также раз непрерывно дифференцируема и на всем промежутке производная .

Введем обозначения: — точка кривой , соответствующая параметру .

Возьмем какую-либо точку на кривой . Дуга также является регулярной кривой класса . Длина дуги кривой определяется как предел периметра ломаной, вписанной в данную дугу, если число звеньев неограниченно возрастает, а длина каждого звена стремится к нулю. Из курса математического анализа известно, что длина дуги вычисляется по формуле

)

или

3. Естественная параметризация.

Определение. Параметризация кривой называется естественной, если модуль производной векторной функции, задающей кривую, равен 1 при любых значениях параметра.

Теорема. Всякая регулярная кривая имеет естественную параметризацию.

Значение натурального параметра равно по величине длине дуги кривой между некоторой точкой, принятой за начальную, и данной точкой; знак натурального параметра определяется в зависимости от выбора направления движения по кривой, условно принятого за положительное.