050201.65 Математика (Информатика)

код наименование

Барнаул

2011

1. Асимптотой плоской кривой называется

   1. предельное положение касательной, точки касания которой неограниченно сближаются

   2. предельное положение касательной, точки касания которой неограниченно удаляются по кривой

   3. прямая, обе точки пересечения которой с кривой удалены в бесконечность

   4. прямая, одна точка пересечения которой с кривой удалена в бесконечность

   5. прямая, лежащая в плоскости кривой, перпендикулярная касательной и проходящая через точку касания

2. Дважды непрерывно дифференцируемая вектор-функция r = r(t) называется бирегулярной если

   1. r'(t) ≠ 0 , r''(t) ≠ 0 ;

   2. (r'(t) , r''(t)) ≠ 0 ;

   3. векторы r'(t) , r''(t) коллинеарны ;

   4. векторы r'(t) , r''(t) неколлинеарны ;

   5. векторы r(t) , r''(t) коллинеарны.

3. Какое из равенств выполняется для векторной функции r = r(s) , где s-натуральный параметр?

   1. (r(s) , dr(s)/ds) = 0 ;

   2. (r(s) , r(s)) = 1 ;

   3. (dr(s)/ds , dr(s)/ds) = 1 ;

   4. (dr(s)/ds , d ²r(s)/ds ²) = 0 ;

   5. (dr(s)/ds , d ²r(s)/ds ², d ³r(s)/ds ³) = 0 .

4. Какое условие должно выполняться для того, чтобы заданная на отрезке [a, b] векторная функция была постоянного модуля

1. r'(t) = 0 ;

2. r'(t) и r(t) ортогональны ;

3. (r(t) , r'(t)) ≠ 0 ;

4. [r(t) , r'(t)] = 0 ;

5. r'(t) и r''(t) параллельны

6. .

1. Найти точку кривой x = 3t - t ³, y = 3t ², z = 3t + t ³ в которой касательная параллельна плоскости 3x + y + z + 2 = 0

1. (2; 3; 4) ;

2. (-2; -3; 4) ;

3. (0; 4; 6) ;

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Алтайская государственная педагогическая академия»

Кафедра

Геометрии и математических методов в экономике

Учебно-методический комплекс дисциплины (модуля)

Геометрия II / 4 (Дифференциальная геометрия)

ОБРАЗЕЦ КОНТРОЛЬНОЙ РАБОТЫ

Специальность

050201.65 Математика (Информатика)

код наименование

Барнаул

2011

Вариант №

1. Составить уравнение касательной к кривой , , в точке .

2. Найти кручение кривой , , в точке .

3. Написать уравнение касательной плоскости к поверхности , , 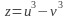в точке Р(3, –1, –7).

4. Найти первую квадратичную форму поверхности , , .

5. Найти полную кривизну поверхности , , в точке Р(3, –1, –7).

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Алтайская государственная педагогическая академия»

Кафедра

Геометрии и математических методов в экономике

Учебно-методический комплекс дисциплины (модуля)

Геометрия II / 4 (Дифференциальная геометрия)

ПЕРЕЧЕНЬ ВОПРОСОВ К ЗАЧЕТУ

Специальность