2.5. Одноканальная система массового обслуживания с неограниченной очередью

Примером одноканальной СМО с неограниченной очередью является одна касса в универмаге.

Пусть поток заявок, поступающих в систему, имеет интенсивность λ, а поток обслуживания – интенсивность μ. Граф состояний подобной системы представлен на рис.3.

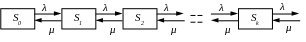
Рис. 3

На рис.3 введены следующие обозначения:

состояние S₀ – канал свободен;

состояние S₁ – канал занят, очереди нет;

состояние S₂ – канал занят, одна заявка стоит в очереди; …;

состояние S_k – канал занят, k-1 заявок стоит в очереди и т.д.

Таким образом, на рис.3 представлен процесс гибели и размножения для бесконечного числа состояний.

В общем случае название процесса гибели и размножения связано с биологией и используется для исследования динамики колебаний численности популяций животных, что возможно в рамках теории массового обслуживания. Граф состояний процесса гибели и размножения представлен на рис.4.

Рис. 4

Система алгебраических уравнений для предельных состояний рассматриваемой СМО имеет вид:

Здесь , где p_i(t) – вероятность того, что в момент времени t СМО находится в состоянии S_i.

Решение полученной системы из n+1 уравнений имеет вид:

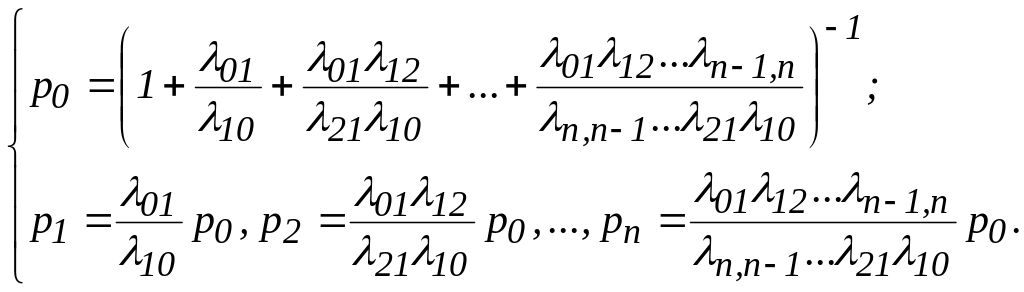(10)

Вернемся к одноканальной СМО с неограниченной очередью. При ее анализе полезно знать положение о конечной величине очереди, которое связано с оценкой предельной интенсивности потока заявок . Если в единицу времени среднее число пришедших заявок меньше среднего числа обслуженных заявок, т.е. ρ<1, то предельные вероятности существуют. Если же ρ>1, то очередь растет до бесконечности. Поэтому предельные вероятности состояний СМО следует искать только в том случае, если ρ<1.

Как следует из первого уравнения системы (10), предельные вероятности СМО, представленной на рис.3, определяются соотношениями

(в скобках стоит сумма бесконечной геометрической прогрессии со знаменателем ρ). Если ρ<1, то эта сумма равна

.

Таким образом, предельная вероятность состояния S₀ СМО определяется соотношением .

Предельная вероятность любого состояния S_k СМО вычисляется по формуле (см. систему (10)):

. (11)

Т.к. ρ<1, то из последнего равенства следует, что вероятность p₀ наибольшая.

Рассмотрим среднее число заявок, находящихся на обслуживании , среднее число заявок в очереди и среднее число заявок в системе . При этом выполняется соотношение

.

Среднее число заявок на обслуживании находят как среднее арифметическое взвешенное от двух состояний: канал свободен и каналом обслуживается одна заявка, т.е.

.

Сомножители 0 и 1 в этой системе означают, что в системе на обслуживании находятся ноль заявок, когда канал свободен, или одна заявка, когда канал занят. Вероятности того, что канал свободен или занят соответственно равны p₀ и 1- p₀. Следовательно

. (12)

Среднее число заявок в системе также определяется по формуле взвешенного арифметического среднего:

.

Сумма называется бесконечной арифметико-геометрической прогрессией и вычисляется по формуле:

.

Таким образом получим

. (13)

Среднее число заявок в очереди найдем как разность двух предыдущих величин:

. 14)

Среднее время нахождения системы в том или ином состоянии равно среднему числу заявок, деленному на интенсивность потока заявок:

Пример. В универмаге имеется одна касса. Интенсивность потока покупателей составляет 0,9 покупателей в минуту. Интенсивность обслуживания покупателей кассой – один покупатель в минуту. Предполагается, что очередь может быть неограниченной длины. Определить показатели эффективности работы кассы и вероятность того, что ожидает своей очереди не более трех покупателей.

Решение. Найдем предельную интенсивность потока заявок:

Т.к. ρ<1, то очередь не может бесконечно возрастать и предельные вероятности существуют.

Предельная вероятность того, что у кассы нет ни одного покупателя

Соответственно вероятность того, что касса занята,

Среднее число заявок на обслуживании, в системе, в очереди найдем по приведенным выше формулам (12-14).

заявок,

заявок,

заявок.

Среднее время нахождения системы в том или ином состоянии будет равно:

мин.;

мин.;

мин.

Вероятность того, что у кассы ожидают не более трех покупателей, складывается из предельных вероятностей того, что у кассы нет покупателей или ожидает один, либо два, либо три покупателя, т.е.

.

Рассчитав предельные вероятности по вышеприведенной формуле, получим:

.