2 Особенности реализации метода локального минимума с использованием метода проекции градиента

2.1 Построение начального приближения

Каждый круг размещается таким образом, чтобы он касался нижней границы полосы и предыдущего круга (рис 2.1).

Рисунок 2.1 – Первое размещение кругов

Координаты первого круга будут: где радиус первого круга (рис. 2.2).

Рисунок 2.2 – Координаты кругов первого размещения

Чтобы получить значение координата второго круга (рис. 3.3) обратимся к следующим формулам:

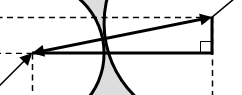
Рисунок 2.3 – Определение координат второго круга

Координаты второго круга будут:

и т.д.

2.2 Вычисления длины шага для линейных ограничений

Произведем вычисления длины шага для линейного ограничения. Для такого вида ограничений будет справедливо следующее:

.

Если – исходная точка, то

,

,

, .

- значение в предыдущей точке , это допустимая точка.

Следовательно .

Если , то в точке ограничения будет выполняться при любом .

Пусть , тогда

,

.

Номер k - того шага:

2.3 Вычисление длины шага для нелинейных ограничений

Произведем вычисления длины шага для нелинейного ограничений. Для такого вида ограничений будет справедливо следующее (рис. 2.4):

Y – Вектор направление;

X – Исходная точка.

Рисунок 2.4 – Размещение кругов

Произведем выбор вектора направления:

,

где

, .

Кроме того, справедливо:

Приводим к виду: , где .

Находим решения и :

1) При и длина шага min (рис 2.5);

Рисунок 2.5 – Представление нахождения длины шага при

2) При длина шага (рис 2.6);

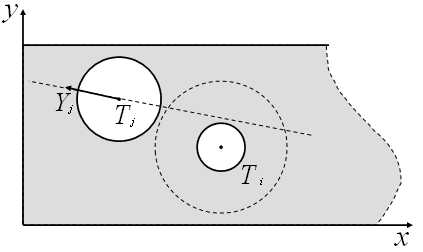
Рисунок 2.6 – Представление не пресекающих кругов при

3) При длина шага (рис 2.7);

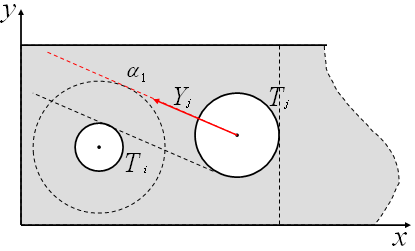
Рисунок 2.7 – Когда круг пройдет через точки касания

2.4 Удаление нелинейных ограничений из матрицы активных ограничений

Если нелинейное ограничение перестает быть активным (рис. 2.8), то из матрицы активных ограничений удаляем соответствующее ему линейное ограничение (рис. 2.9).

После изменения точки размещения, удаляем из матрицы активных ограничений, те которые перестали быть активными.

Рисунок 2.8 – Движение кругов за направлением

Рисунок 2.9 – Удаление соответствующего не активного ограничения

2.5 Иллюстрация процесса движения

Покажем как размещается каждый круг с первого до конечного размещения и как он двигается, и при этом получаем по каждому шагу новое оптимальное решение. Получим допустимое начальное размещения для трех кругов (рис. 2.10, а-е).

а

б

в

г

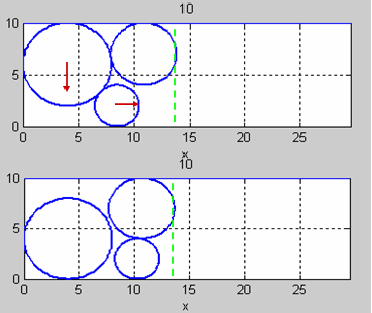
д

е

Рисунок 2.10 – Допустимое начальное до конечного размещения для трех кругов: а – первый шаг; б – второй шаг; в – пятый шаг; г – шестой шаг;

д – девятый шаг; е – десятый шаг