2. Задача
Система состоит из пяти последовательно соединенных элементов, данные об их надежности приведены в таблице 2.1.
Таблица 2.1.
Элементы |
||||
1 |
2 |
3 |
4 |
5 |
TN( |
R( |
W( |
Exp( |
Г(9,85) |
)
)
)
)
Требуется определить:
- вероятность безотказной работы системы;
- среднее время безотказной работы системы;
- интенсивность отказов системы;
- плотность распределения времени до отказа системы;
Решение
Определим математическое ожидание и среднее квадратическое отклонение времени до отказа элементов.
Элемент 1. Усеченное нормальное распределение с параметрами
и
:
Элемент 2. Распределение Рэлея с параметром
:
Элемент 3. Распределение Вейбулла с параметром формы
и параметром масштаба
:
Элемент 4. Экспоненциальное распределение с параметром
Элемент 5. Гамма-распределение с параметром формы
и параметром масштаба
:
Полученные значения сведены в табл. 2.2.
Таблица 2.2. Параметры законов распределения времени до отказа элементов
Номер элемента |
1 |
2 |
3 |
4 |
5 |
Среднее время безотказной работы, час |
380 |
222 |
196 |
5000 |
765 |
Среднее квадратическое отклонение времени безотказной работы, час |
100 |
116 |
73 |
5000 |
255 |
Вычислим вероятность безотказной работы элементов.
Элемент 1. Усеченное нормальное распределение с параметрами и
Элемент 2. Распределение Рэлея с параметром :
Элемент 3. Распределение Вейбулла с параметром формы и параметром масштаба :
Элемент 4. Экспоненциальное распределение с параметром
Элемент 5. Гамма-распределение с параметром формы и параметром масштаба :
Табулируя эти функции от 0 до 1000 часов с шагом 40 часов, получим табл. 2.3.
Таблица 2.3. Вероятность безотказной работы элементов
t, час |
|
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
40 |
0.9997354 |
0.974725 |
0.999991 |
0.99203191 |
1 |
0.966694 |
80 |
0.998722358 |
0.902668 |
0.998836 |
0.98412732 |
0.999999 |
0.886173 |
120 |
0.995410828 |
0.794216 |
0.980302 |
0.97628571 |
0.999983 |
0.756607 |
160 |
0.9861679 |
0.663916 |
0.861534 |
0.96850658 |
0.999847 |
0.546226 |
200 |
0.964139434 |
0.527292 |
0.491309 |
0.96078944 |
0.999248 |
0.239799 |
240 |
0.919309851 |
0.397882 |
0.078355 |
0.95313379 |
0.99743 |
0.027247 |
280 |
0.84140562 |
0.285247 |
0.000558 |
0.94553914 |
0.993164 |
0.000126 |
320 |
0.725799392 |
0.194291 |
5.19E-09 |
0.938005 |
0.98485 |
6.76E-10 |
360 |
0.579301621 |
0.125732 |
1.27E-19 |
0.9305309 |
0.970776 |
8.36E-21 |
400 |
0.420770733 |
0.077305 |
3.11E-40 |
0.92311635 |
0.949427 |
8.88E-42 |
440 |
0.274272961 |
0.045157 |
1.03E-77 |
0.91576088 |
0.919775 |
1.07E-79 |
480 |
0.158666733 |
0.025062 |
2.8E-142 |
0.90846402 |
0.881461 |
8.8E-145 |
520 |
0.080762502 |
0.013215 |
1.3E-248 |
0.9012253 |
0.834855 |
1E-251 |
560 |
0.035932919 |
0.00662 |
0 |
0.89404426 |
0.780984 |
0 |
600 |
0.013904453 |
0.003151 |
0 |
0.88692044 |
0.72139 |
0 |
640 |
0.004661525 |
0.001425 |
0 |
0.87985338 |
0.657924 |
0 |
680 |
0.001349996 |
0.000612 |
0 |
0.87284263 |
0.592547 |
0 |
720 |
0.000336954 |
0.00025 |
0 |
0.86588775 |
0.527153 |
0 |
760 |
7.23533E-05 |
9.69E-05 |
0 |
0.85898828 |
0.463428 |
0 |
800 |
1.33467E-05 |
3.57E-05 |
0 |
0.85214379 |
0.402765 |
0 |
840 |
2.11261E-06 |
1.25E-05 |
0 |
0.84535383 |
0.346221 |
0 |
880 |
2.86672E-07 |
4.16E-06 |
0 |
0.83861798 |
0.29451 |
0 |
920 |
3.33229E-08 |
1.31E-06 |
0 |
0.8319358 |
0.248032 |
0 |
960 |
3.31599E-09 |
3.95E-07 |
0 |
0.82530687 |
0.206912 |
0 |
1000 |
2.82336E-10 |
1.13E-07 |
0 |
0.81873075 |
0.171057 |
0 |
На
рис. 2.1 показаны графики функций
,
соответствующих вероятностям безотказной
работы элементов. На рис. 2.2 изображен
график безотказной работы системы
.
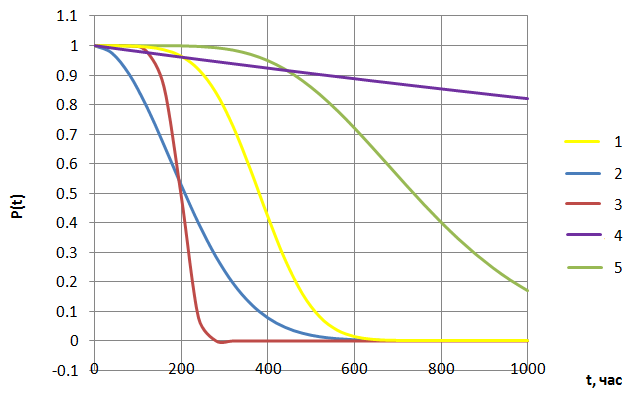
Рис. 2.1. Вероятности безотказной работы элементов
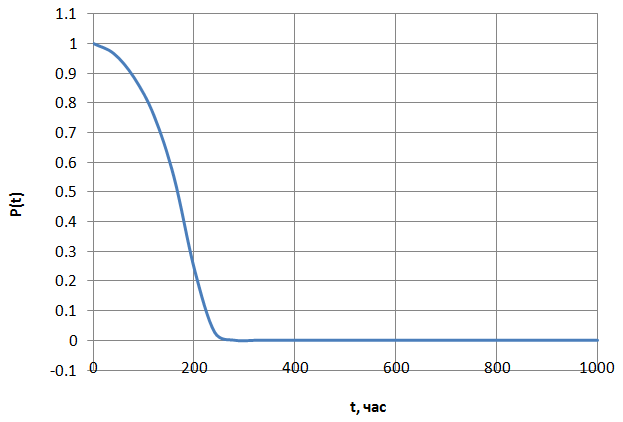
Рис. 2.2. Вероятности безотказной работы системы
Из графиков видно, что при большом времени работы системы наиболее надежным оказывается 4 элемент системы.
Вычислим среднее время безотказной работы системы:
по формуле Симпсона:
183,6 час.
где n - число точек, h - шаг интегрирования, выбираемый из условия обеспечения требуемой точности.
На рис. 2.3. изображены графики интенсивностей отказов элементов. Кривая 4, соответствующая экспоненциальному закону имеет постоянную интенсивность отказа. Все остальные кривые интенсивностей отказов являются возрастающими функциями времени.
На рис. 2.4 показан график интенсивности отказа системы, равной сумме интенсивностей отказов ее элементов:
Рис. 2.3. Интенсивности отказов элементов
Рис. 2.4. Интенсивность отказа системы
Интенсивность отказа системы также является возрастающей функцией времени, что говорит о том, что система является стареющей, а закон распределения времени до ее отказа не экспоненциальный.
Вычислим плотности распределения вероятностей времени безотказной работы элементов.
Элемент 1. Усеченное нормальное распределение с параметрами и
Элемент 2. Распределение Рэлея с параметром :
Элемент 3. Распределение Вейбулла с параметром формы и параметром масштаба :
Элемент 4. Экспоненциальное распределение с параметром
Элемент 5. Гамма-распределение с параметром формы и параметром масштаба :
Табулируя плотности распределения от 0 до 2000 часов с шагом 100 часов получим табл. 2.4.
Таблица 2.4. Плотности распределения времени безотказной работы элементов
t, час |
|
|
|
|
|
0 |
5.83894E-06 |
0 |
0 |
0.0002 |
0 |
40 |
1.23222E-05 |
0.001248 |
1.02E-06 |
0.00019841 |
4.38E-10 |
80 |
4.43185E-05 |
0.002311 |
6.54E-05 |
0.00019683 |
7.01E-08 |
120 |
0.00013583 |
0.00305 |
0.000731 |
0.00019526 |
1.12E-06 |
160 |
0.000354746 |
0.003399 |
0.003611 |
0.0001937 |
7E-06 |
200 |
0.000789502 |
0.003375 |
0.007856 |
0.00019216 |
2.61E-05 |
240 |
0.001497275 |
0.003056 |
0.003741 |
0.00019063 |
7E-05 |
280 |
0.002419707 |
0.002556 |
6.72E-05 |
0.00018911 |
0.00015 |
320 |
0.003332246 |
0.00199 |
1.39E-09 |
0.0001876 |
0.000273 |
360 |
0.003910427 |
0.001448 |
6.91E-20 |
0.00018611 |
0.000437 |
400 |
0.003910427 |
0.00099 |
3.19E-40 |
0.00018462 |
0.000635 |
440 |
0.003332246 |
0.000636 |
1.87E-77 |
0.00018315 |
0.00085 |
480 |
0.002419707 |
0.000385 |
8.4E-142 |
0.00018169 |
0.001065 |
520 |
0.001497275 |
0.00022 |
6.3E-248 |
0.00018025 |
0.001261 |
560 |
0.000789502 |
0.000119 |
0 |
0.00017881 |
0.001426 |
600 |
0.000354746 |
6.05E-05 |
0 |
0.00017738 |
0.001546 |
640 |
0.00013583 |
2.92E-05 |
0 |
0.00017597 |
0.001619 |
680 |
4.43185E-05 |
1.33E-05 |
0 |
0.00017457 |
0.001642 |
720 |
1.23222E-05 |
5.76E-06 |
0 |
0.00017318 |
0.00162 |
760 |
2.91947E-06 |
2.36E-06 |
0 |
0.0001718 |
0.00156 |
800 |
5.89431E-07 |
9.14E-07 |
0 |
0.00017043 |
0.001469 |
840 |
1.01409E-07 |
3.36E-07 |
0 |
0.00016907 |
0.001355 |
880 |
1.48672E-08 |
1.17E-07 |
0 |
0.00016772 |
0.001228 |
920 |
1.85736E-09 |
3.87E-08 |
0 |
0.00016639 |
0.001095 |
960 |
1.97732E-10 |
1.21E-08 |
0 |
0.00016506 |
0.000961 |
1000 |
1.79378E-11 |
3.6E-09 |
0 |
0.00016375 |
0.000832 |
Графики, построенные по данным табл. 2.4, приведены на рис. 2.5.
Рис. 2.5. Плотности распределения времени до отказа элементов
Плотность
распределения времени до отказа системы
изображена на рис. 2.6. Для ее изображения
вычисления выполнялись по формуле:
Из графика отчетливо видна неэкспоненциальность распределения времени до отказа нерезервированной системы, если законы распределения времени до отказа ее элементов не являются экспоненциальными.
Рис. 2.6. Плотности распределения времени до отказа системы