
- •3.Вычислительные методы линейной алгебры
- •3.1.Нормы векторов и матриц
- •3.2.Решение систем линейных алгебраических уравнений
- •3.2.1.Метод Гаусса для решения систем линейных уравнений
- •3.2.2.Итерационный метод
- •3.2.3.Метод Зейделя
- •3.2.4.Погрешность решения и обусловленность системы уравнений
- •3.3.Вычисление определителя и обратной матрицы
- •3.4.Собственные числа и собственные векторы матрицы
- •3.4.1.Метод скалярных произведений
- •3.4.2.Вычисление всех собственных значений положительно определенной симметричной матрицы
3.4.1.Метод скалярных произведений
Рассмотрим метод скалярных произведений [7] для определения наибольшего собственного значения и соответствующего собственного вектора действительной матрицы A.
Теорема 3.10. Транспонированная матрица AT имеет те же собственные значения, что и матрица A. Пусть λi и λk — различные собственные значения матрицы A (и транспонированной матрицы AT), а xi — собственный вектор матрицы A, отвечающий собственному значению λi, а yk — собственный вектор матрицы AT, отвечающий собственному значению λk. Тогда векторы xi и xk — ортогональны.
Пусть требуется вычислить наибольшее собственное значение и соответствующий собственный вектор действительной матрицы A. В методе скалярных произведений вместе с матрицей A используется транспонированная матрица AT.
Алгоритм метода скалярных произведений.
1. Зададим начальные приближения: x0 — к собственному вектору матрицы A и y0 = x0 — к собственному вектору транспонированной матрицы AT; k = 0;
2. Вычисляем (k + 1)-е приближение к наибольшему собственному значению λ по формулам:
![]() (3.41)
(3.41)
3. Если |λk+1 – λk| ≥ ε, переходим к пункту 2, иначе — к 4;
4. Конец.
3.4.2.Вычисление всех собственных значений положительно определенной симметричной матрицы
Приведем алгоритм для вычисления нескольких первых или всех собственных значений и соответствующих собственных векторов положительно определенной симметричной матрицы.
Пусть уже вычислены первые m собственных значений λ1, λ2, …, λm и m соответствующих собственных векторов x1, x2, …, xm.
Алгоритм вычисления очередного (m + 1)-го собственного значения и соответствующего собственного вектора.
0. Выберем начальное приближение
![]() ;
k = 0;
;
k = 0;
1. Вычисляем k-е приближение к собственному значению λm+1:
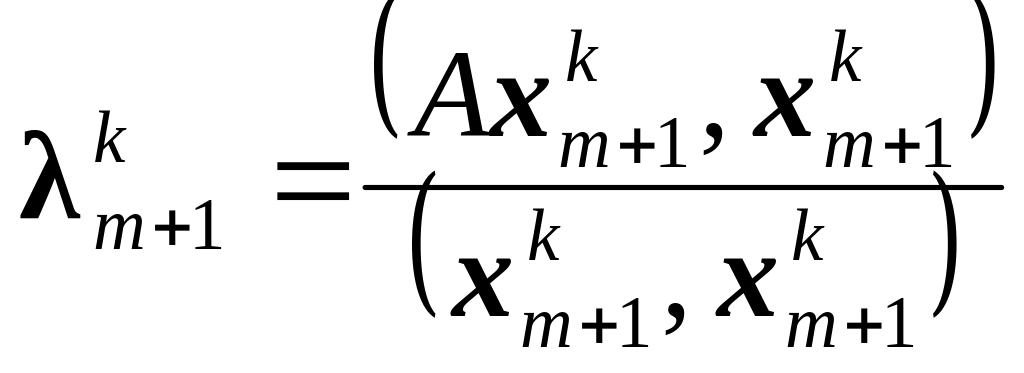 ;
(3.42)
;
(3.42)
2. Находим вектор
![]() из
уравнения
из
уравнения
![]() ;
(3.43)
;
(3.43)
3. Если m > 0
ортогонализируем вектор
![]() к первым m собственным
векторам
к первым m собственным
векторам
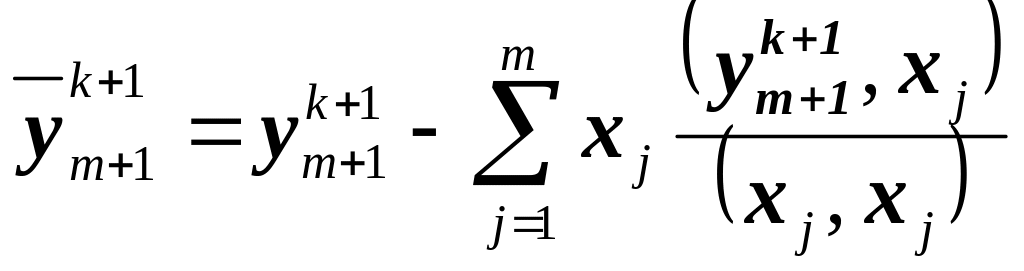 (3.44)
(3.44)
4. Нормируем полученный вектор
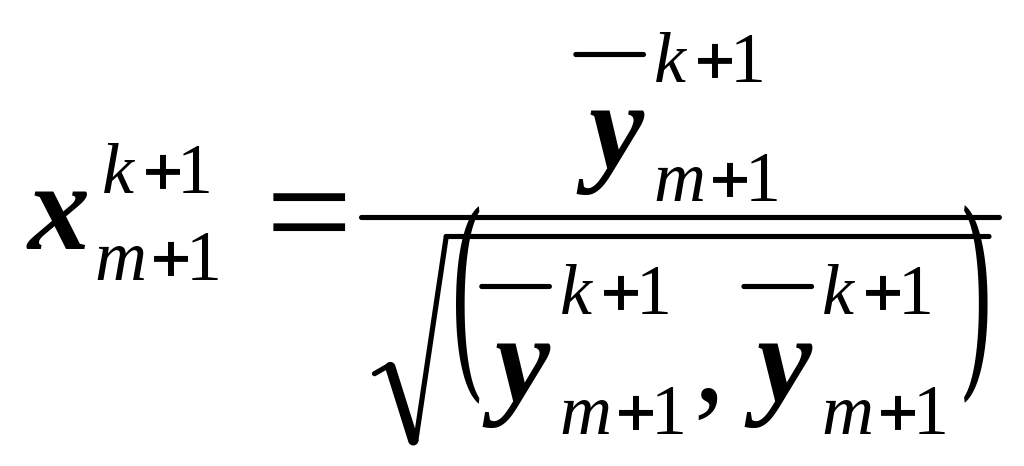 (3.45)
(3.45)
5. k = k + 1;
Процесс 1. —5. повторяется до тех пор, пока не будет выполнено условие сходимости итераций
![]() ,
(3.46)
,
(3.46)
где ε – заданная погрешность.
При вычислении первого собственного значения и соответствующего вектора пункт 3) пропускается.
Этим алгоритмом можно вычислить все собственные значения и собственные векторы.
Пример 3.11. Найти все собственные значения и соответствующие собственные векторы матриц:
1)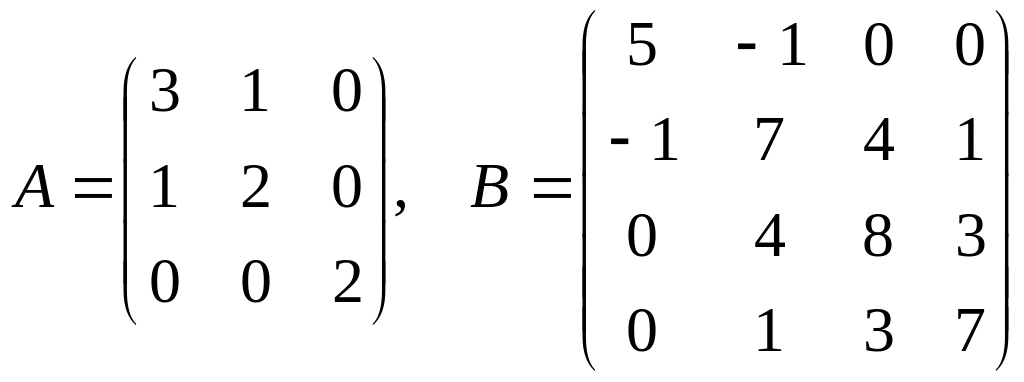 .
.
Решение с помощью программы на языке C++. Реализуем алгоритм (3.42) — (3.46) на языке C++ и проверим программу на данном примере, сравнивая полученный результат с ответами из примеров 3.9, 3.10.
Текст программы приведен ниже:
#include <iostream.h>
#include <except.h>
#include <stdlib.h>
#include <math.h>
int Eigen(long double **a, long double **x, long double *eigv,
long double eps, const int n, int k_max);
long double s_prod(long double *x1, long double *x2, const int n);
int gauss(long double **a, long double *b, long double *x, const int n);
int main(){
long double **a, **x, *eigv, eps; int i,j,n,k_max;
cout <<"\n input n = " ; cin >> n;
cout <<"\n input k_max = " ; cin >> k_max;
cout <<"\n input eps = " ; cin >> eps;
try {
a = new long double*[n]; for(i=0;i<n;i++) a[i]=new long double[n];
x = new long double*[n]; for(i=0;i<n;i++) x[i]=new long double[n];
eigv = new long double[n];
}
catch (xalloc){cout <<"\nCould not allocate\n"; exit(-1);}
cout <<"\n input matrix a: \n";
for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> a[i][j];
cout <<"\n matrix a:";
for (i=0; i<n; i++){
cout << "\n ";for (j=0; j<n; j++)cout <<" "<< a[i][j];}
Eigen(a, x, eigv, eps, n, k_max);
for(i = 0; i < n; i++)cout << "\n Eigen Value [" << i << "] = " << eigv[i];
cout << "\n Eigen Vectors: " ;
for (i=0; i<n; i++){
cout <<"\n "; for (j=0; j<n; j++) cout << " " << x[i][j];}
cout <<"\n ";
cin >> i; // for pause
for(i = 0; i < n; i++) delete[] a[i];
delete a;
for(i = 0; i < n; i++) delete[] x[i];
delete x;
delete[] eigv;
return 0;
}//end main --------------------------------------------------------------
int Eigen(long double **a, long double **x, long double *eigv,
long double eps, const int n, int k_max){
int i, j, k, m;
long double **a1,*x0,*x1,*alf, xerr, xnrm, eig0, eig1,s;
a1 = new long double*[n]; for(i=0;i<n;i++) a1[i]=new long double[n];
x0 = new long double[n]; x1 = new long double[n];
alf = new long double[n];
for(m = 0; m < n; m++){
// 0.
k = 0; for(i = 0; i < n; i++)x0[i] = 1. ; eig0 = 0;
do {
// 1.
for(i = 0; i < n; i++){s = 0;
for(j = 0; j < n; j++)s += a[i][j]*x0[j]; x1[i] = s;}
eig1 = s_prod(x1,x0,n)/s_prod(x0,x0,n);
// 2.
for(i = 0; i < n; i++)x1[i] = eig1*x0[i];
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)a1[i][j] = a[i][j];
gauss(a1,x1,x0,n);
// 3.
if(m > 0){
for(j = 0; j < m ; j++){
for(i = 0; i < n; i++)x1[i] = x[i][j];
alf[j] = s_prod(x0,x1,n)/s_prod(x1,x1,n);
}
for(i = 0; i < n; i++)
for(j = 0; j < m; j++)x0[i]= x0[i] - x[i][j]*alf[j];
}// end if
// 4.
xnrm = sqrt(s_prod(x0,x0,n));
for(i = 0; i < n; i++)x0[i] = x0[i] / xnrm;
xerr = fabs(eig1 - eig0); eig0 = eig1;
k = k + 1; if (k > k_max)break;
}while (xerr > eps);
eigv[m] = eig1;
for(i = 0; i < n; i++) x[i][m] = x0[i];
}// end m
for(i = 0; i < n; i++) delete[] a1[i];
delete a1;
delete[] x0;
delete[] x1;
delete[] alf;
return 0;
}// end Eigen
long double s_prod(long double *x1, long double *x2, const int n){
long double s; int i; s = 0;
for(i = 0; i < n; i++)s = s + x1[i]*x2[i];
return s;
}// end s_prod
int gauss(long double **a, long double *b, long double *x, const int n){
int i, k, m; long double amm, aim;
for (m = 0; m <= n-2; m++) {// m
amm = a[m][m];
for (k = m; k <= n-1; k++)a[m][k] = a[m][k]/amm; // 3.16
b[m] = b[m] / amm; //
for (i = m + 1; i <= n-1; i++){// i
aim = a[i][m];
for (k = m; k <= n-1; k++)
a[i][k] = a[i][k] - a[m][k]*aim; // 3.17
b[i] = b[i] - b[m]*aim; //
}// end i
}// end m
x[n-1] = b[n-1]/a[n-1][n-1]; // 3.19
for (i = n - 2; i >= 0; i--){// i
x[i] = b[i]; //
for (k = i + 1; k < n; k++) // 3.20
x[i] = x[i] - a[i][k]*x[k]; //
}// end i
return 0;
}// end gauss
Приведем результаты расчетов:
1) Для матрицы A:
Input n = 3
Input k_max = 100
Input eps = 0.001
Input matrix a:
3 1 0 1 2 0 0 0 2
matrix a:
3 1 0
1 2 0
0 0 2
Eigen Value [0] = 1.38279
Eigen Value [1] = 1.99985
Eigen Value [2] = 3.61796
Eigen Vectors:
-0.525551 0.0189405 0.850551
0.850389 -0.0179017 0.52585
0.0251862 0.99966 -0.00669857
2) Для матрицы B:
Input n = 4
Input k_max = 1000
Input eps = 0.0000001
Input matrix a:
5 -1 0 0 -1 7 4 1 0 4 8 3 0 1 3 7
matrix a:
5 -1 0 0
-1 7 4 1
0 4 8 3
0 1 3 7
Eigen Value [0] = 2.79088
Eigen Value [1] = 4.87123
Eigen Value [2] = 6.31445
Eigen Value [3] = 13.0234
Eigen Vectors:
0.279353 0.861671 0.41803 -0.0688165
0.617008 0.110771 -0.549768 0.552074
-0.660456 0.261569 0.018022 0.703602
0.324131 -0.420517 0.722967 0.442067
Приведем для дополнительной проверки правильности работы программы результаты расчета собственных значений и собственных векторов я матрицы B в программе Mathcad:
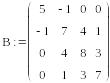
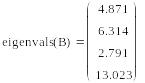
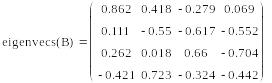
Сравнив эти результаты, можно сделать вывод о корректности работы программы и правильности алгоритма (3.42) — (3.46).
Замечание. Так как программа носит учебный характер, интерфейс программы сделан простым, достаточным на наш взгляд для понимания алгоритма. В частности, если размерность матрицы больше четырех, то вывод матрицы на экран может быть не таким наглядным (строка матрицы может не поместиться в одну строку экрана). В этом случае студентам предлагается изменить программу в соответствующей части.
Задачи для самостоятельного решения.
Решить систему линейных уравнений Ax = b в электронных таблицах методом Гаусса. Вычислить определитель матрицы A методом Гаусса. Найти обратную матрицу A–1 методом Гаусса.
1.
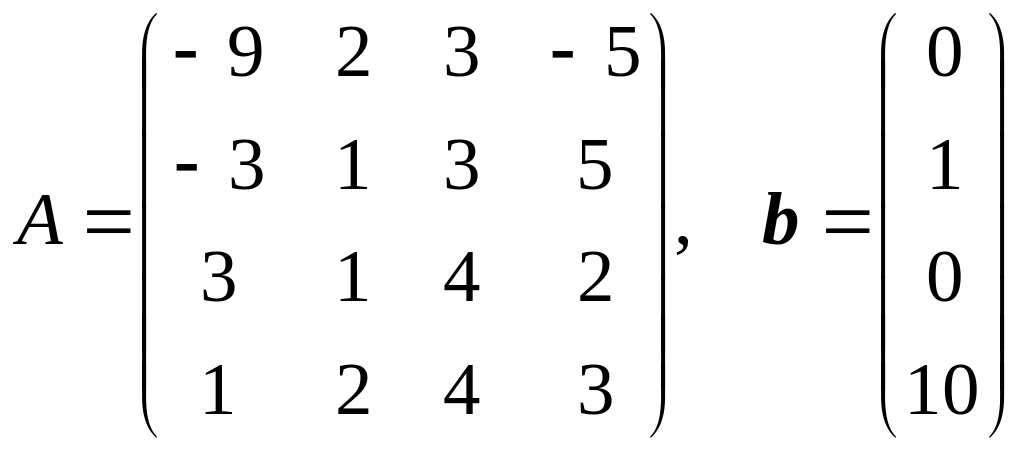 .
2.
.
2.
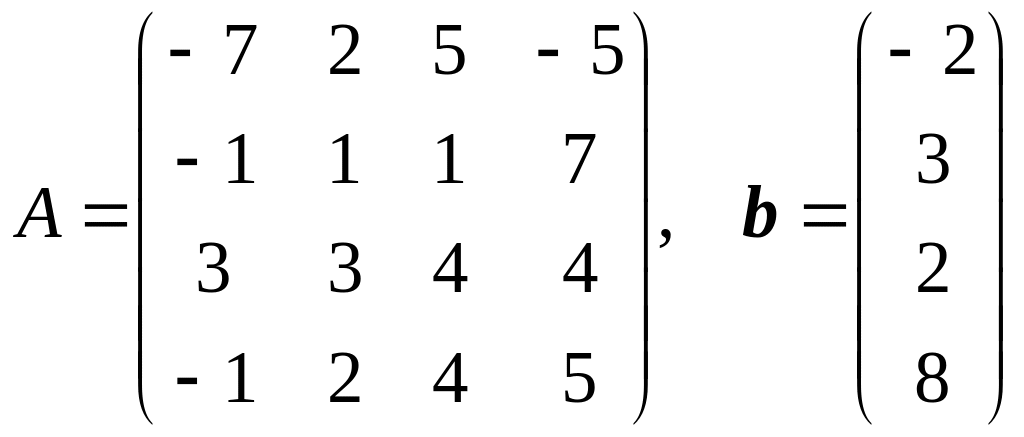 .
.
3.
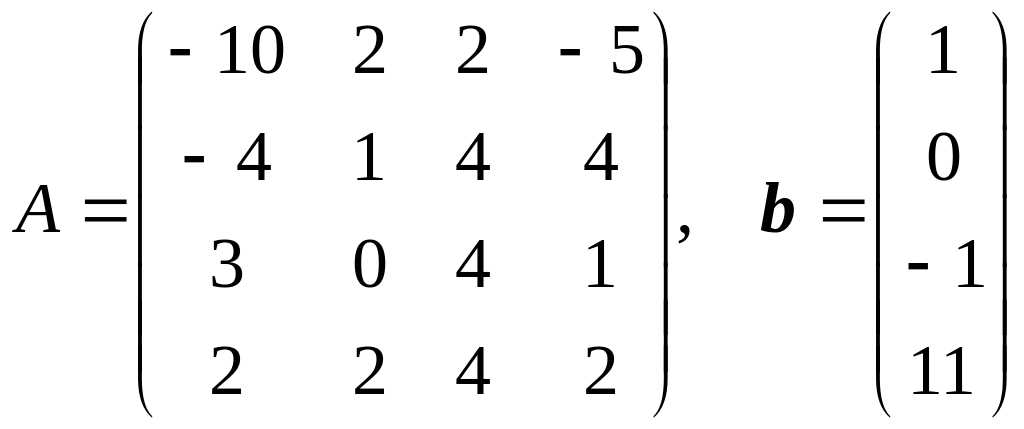 .
4.
.
4.
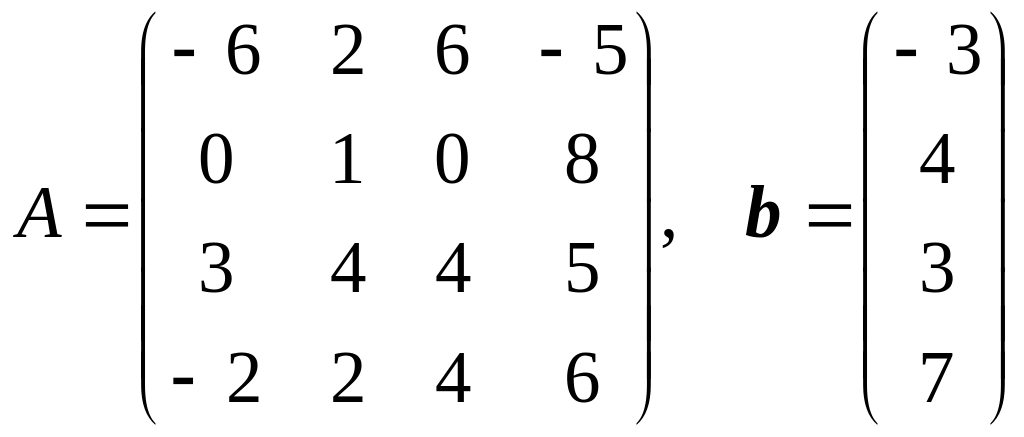 .
.
5.
 .
6.
.
6.
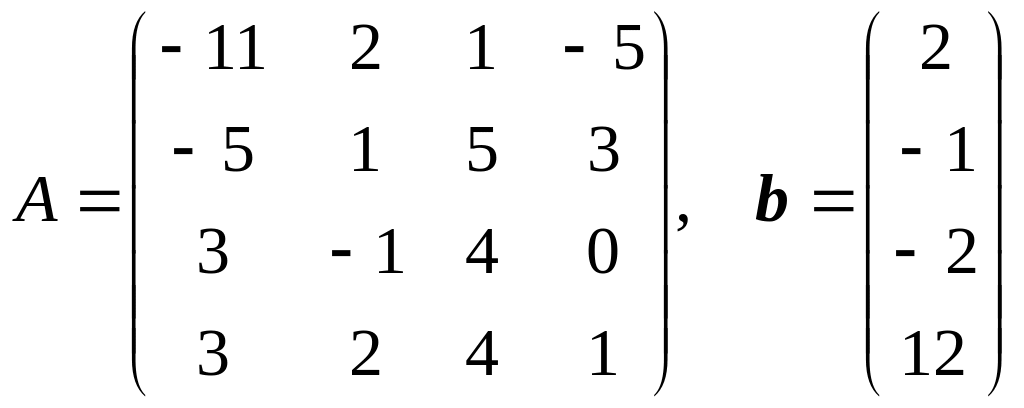 .
.
7.
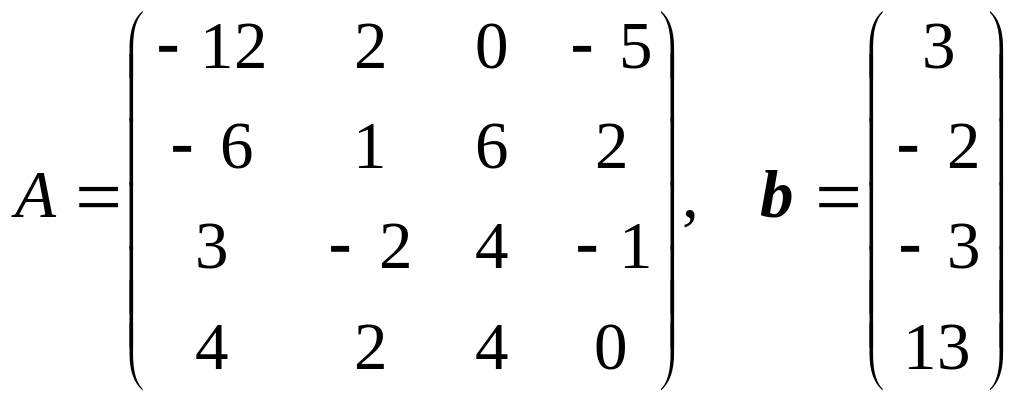 .
8.
.
8.
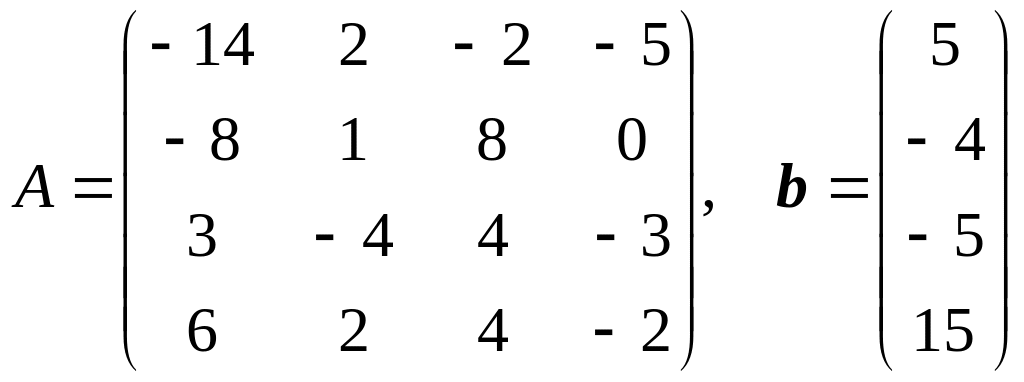 .
.
9.
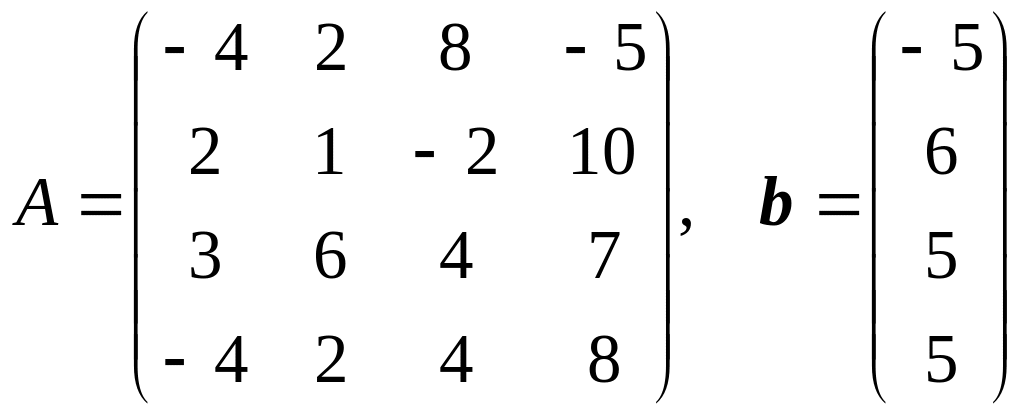 .
10.
.
10.
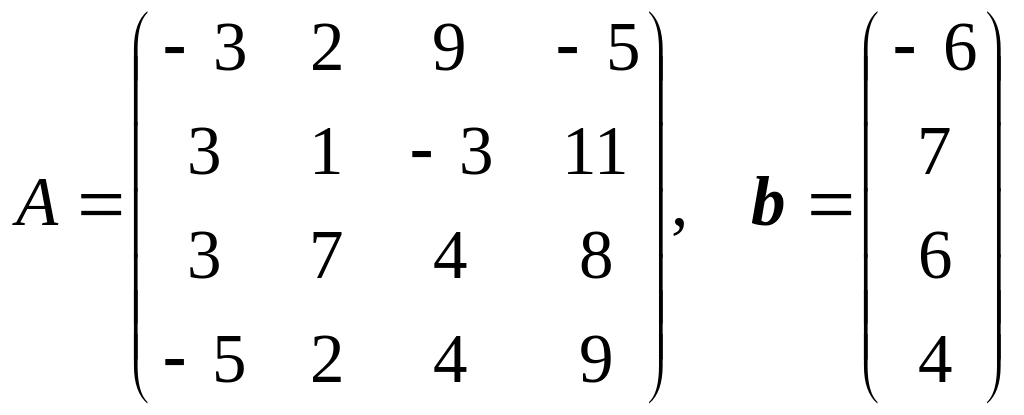 .
.
11.
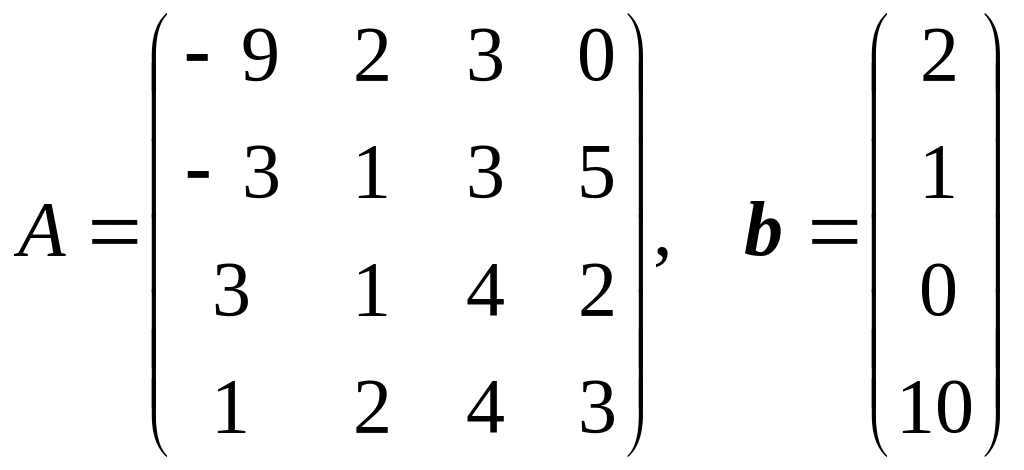 .
12.
.
12.
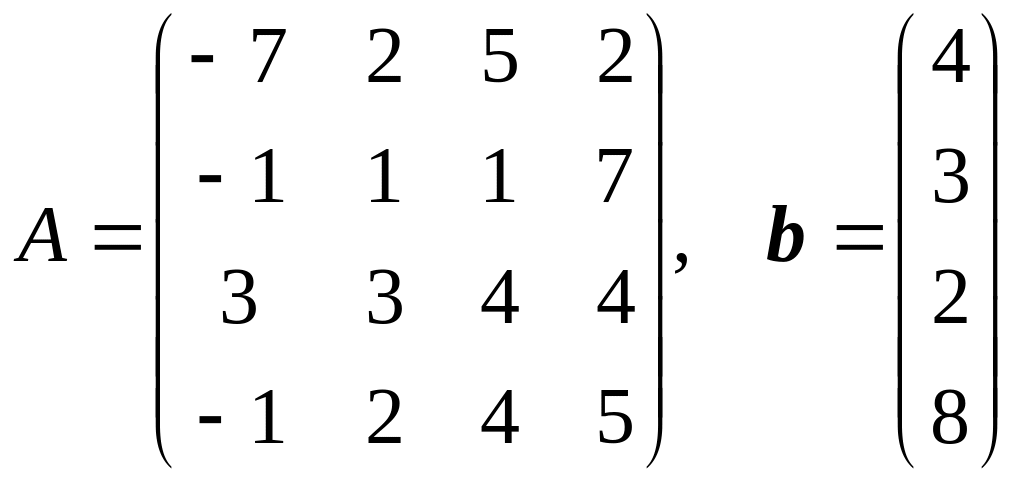 .
.
13.
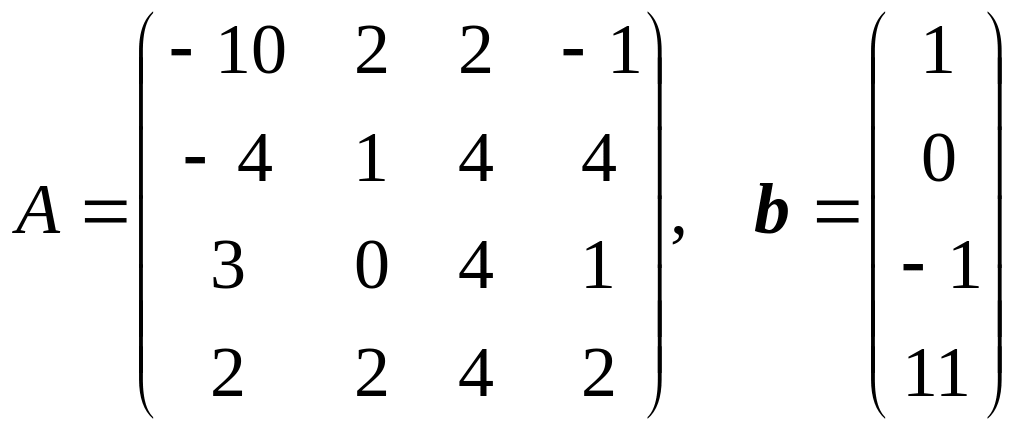 .
14.
.
14.
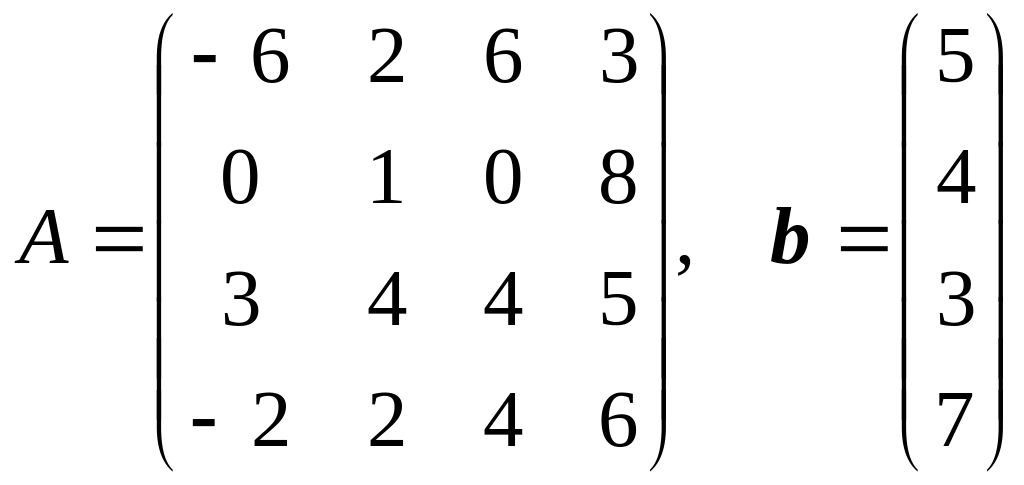 .
.
15.
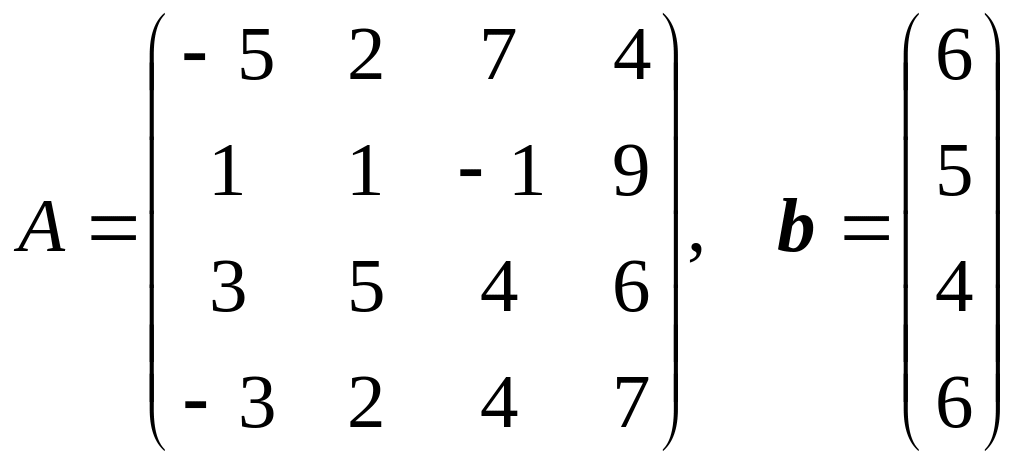 ,
16.
,
16.
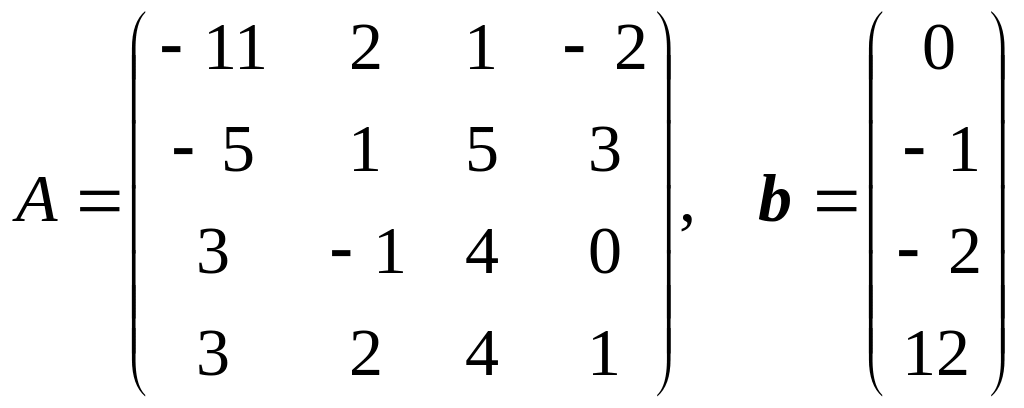
17.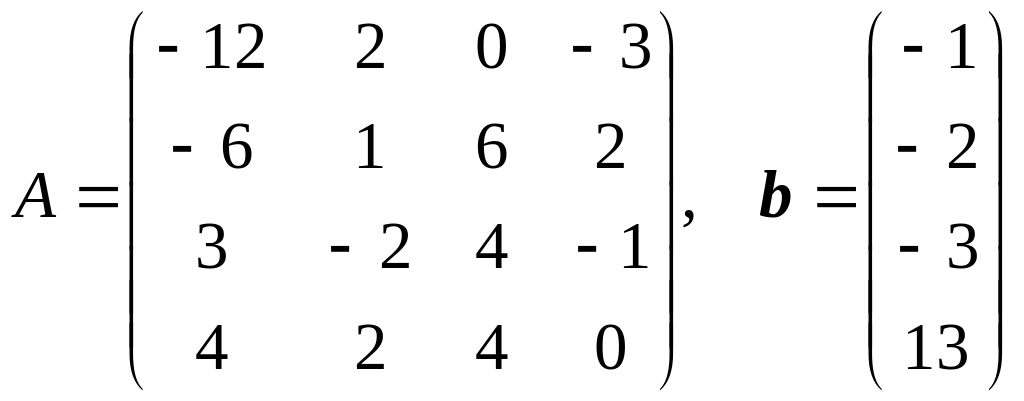 .
18.
.
18.
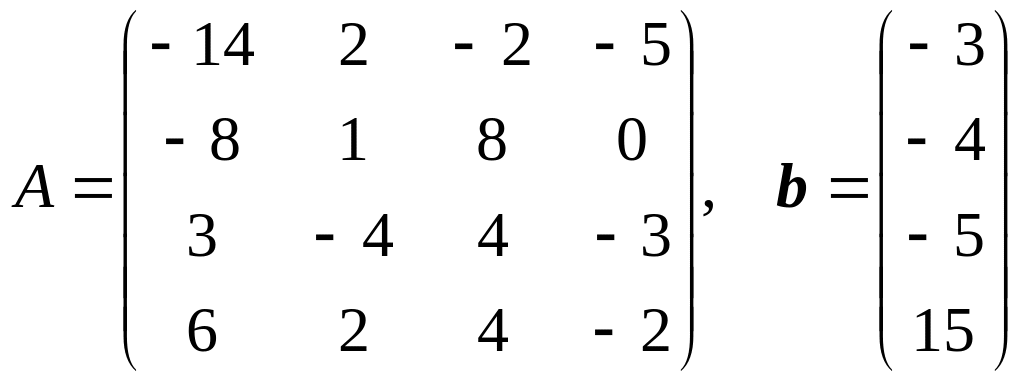 .
.
19.
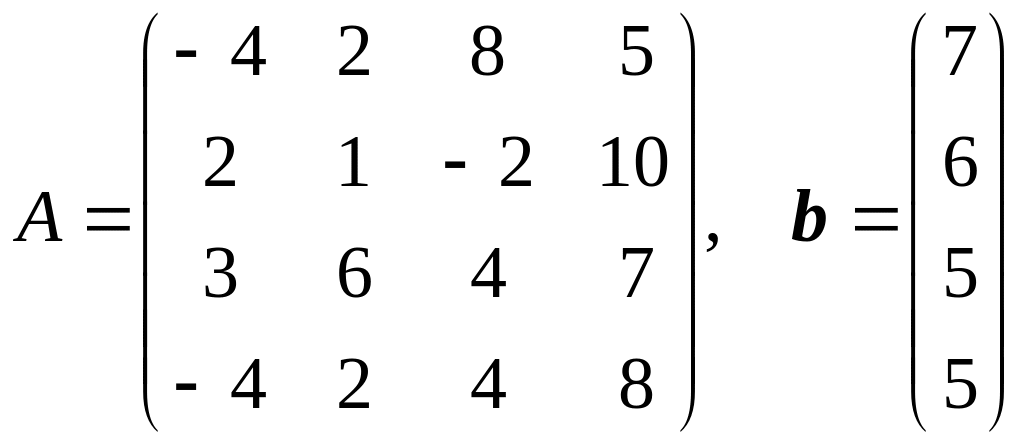 .
20.
.
20.
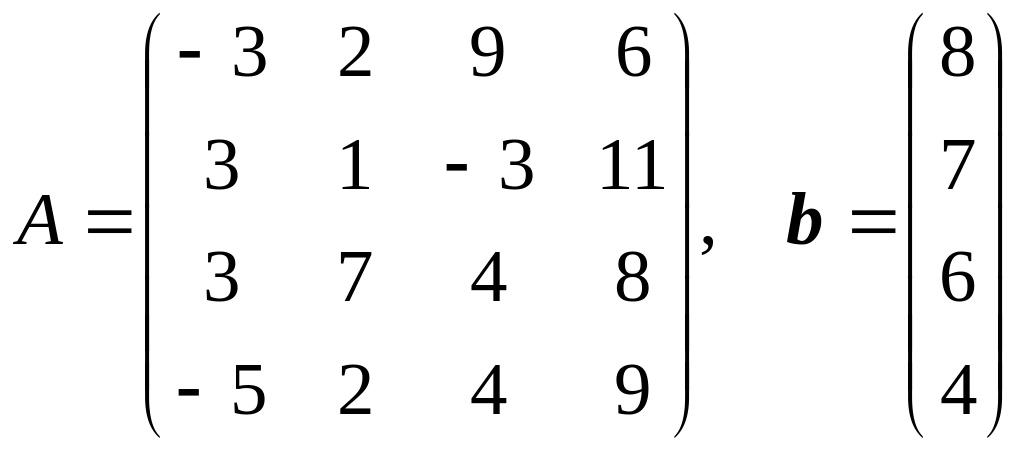 .
.
Для данных систем линейных уравнений проверить условие сходимости метода итераций и решить их.
21.
![]() 22.
22.
![]()
23.
![]() 24.
24.
![]()
25.
![]() 26.
26.
![]()
27.
![]() 28.
28.
![]()
29.
![]() 30.
30.
![]()
Решить системы линейных уравнений методом Зейделя, если выполняется условие сходимости.
31.
![]() 32.
32.
![]()
33.
![]() 34.
34.
![]()
35.
![]() 36.
36.
![]()
37.
![]() 38.
38.
![]()
39.
![]() 40.
40.
![]()
Для заданных матриц а) составить характеристическое уравнение и найти собственные значения; б) найти собственные векторы.
41.
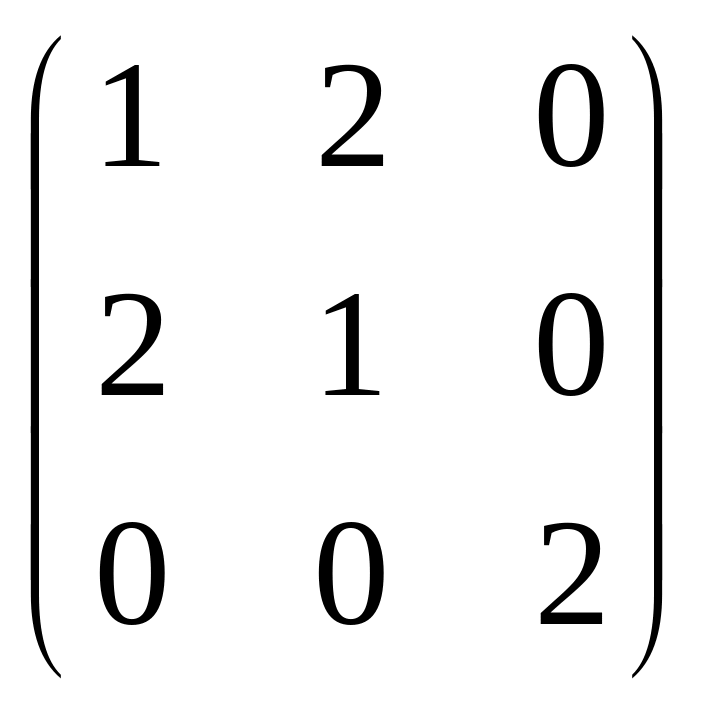 .
42.
.
42.
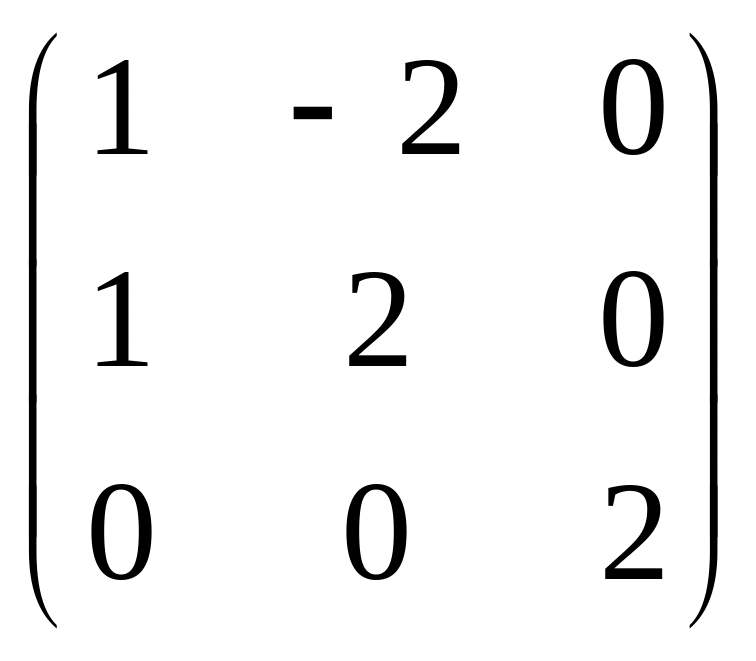 .
43.
.
43.
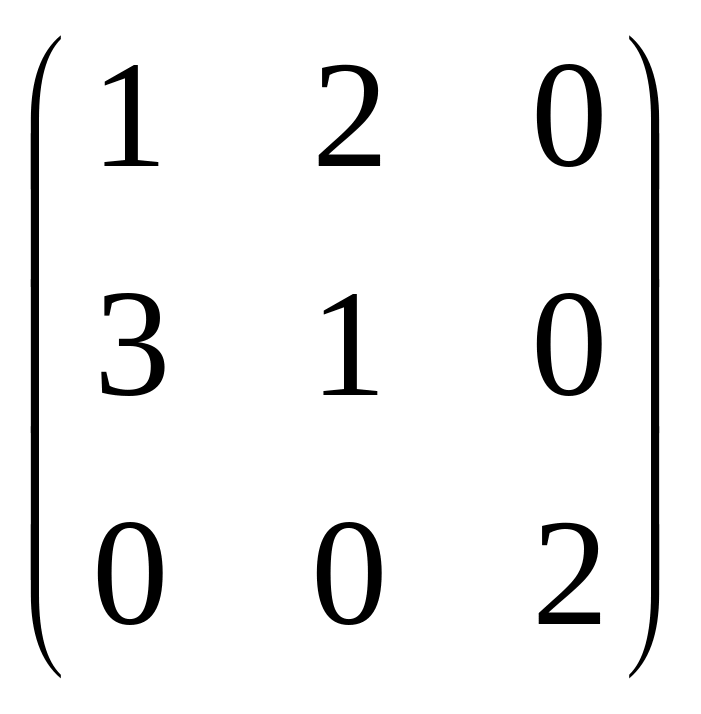 .
44.
.
44.
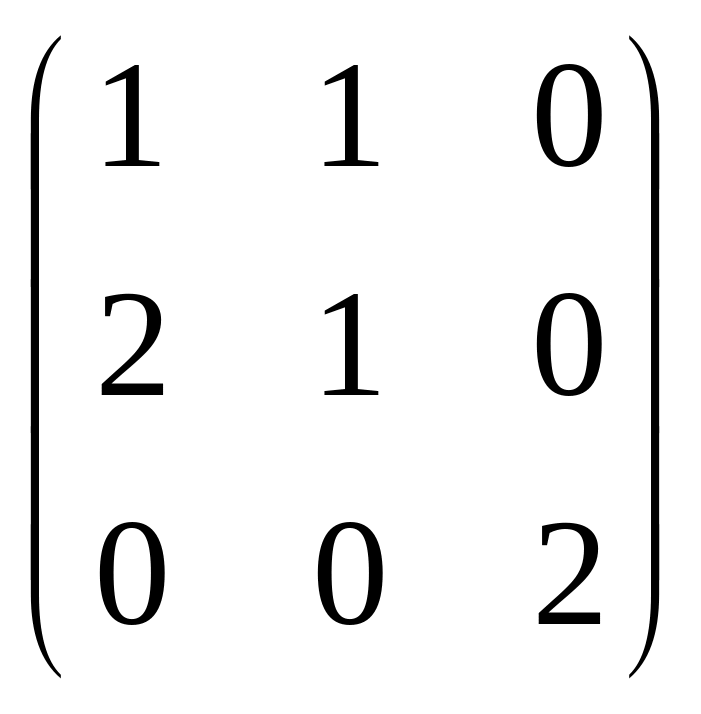 .
45.
.
45.
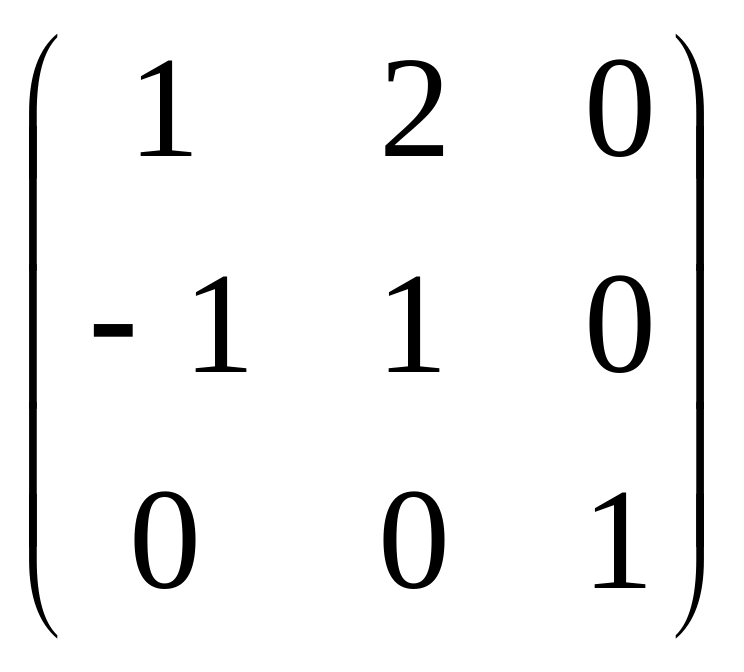 .
.
46.
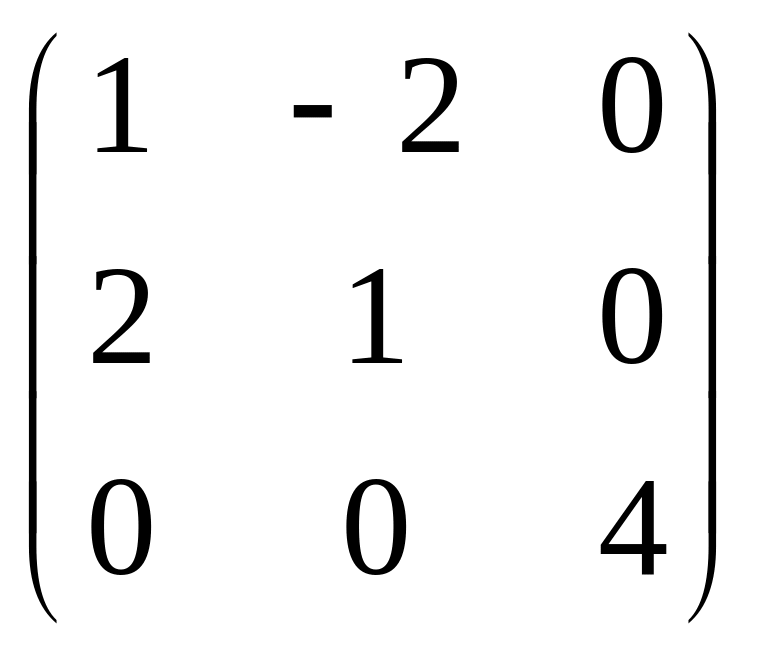 .
47.
.
48.
.
47.
.
48.
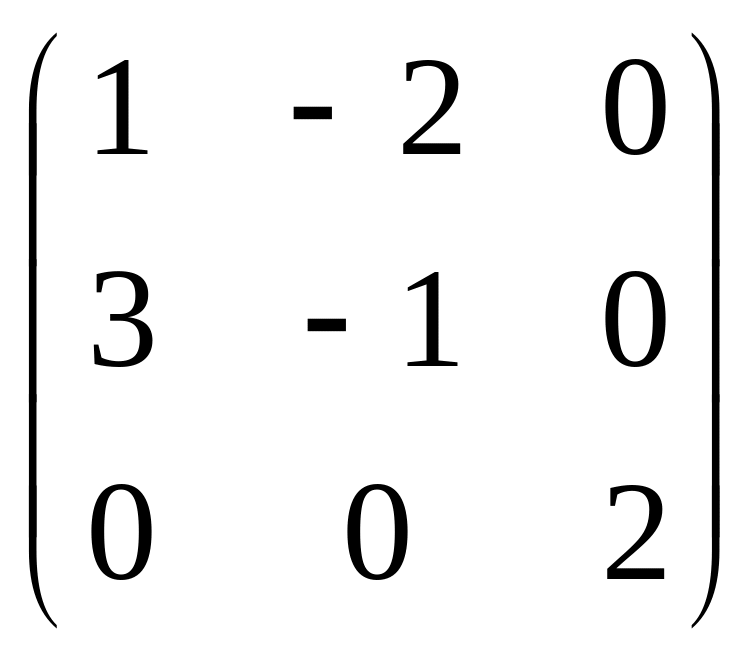 .
49.
.
49.
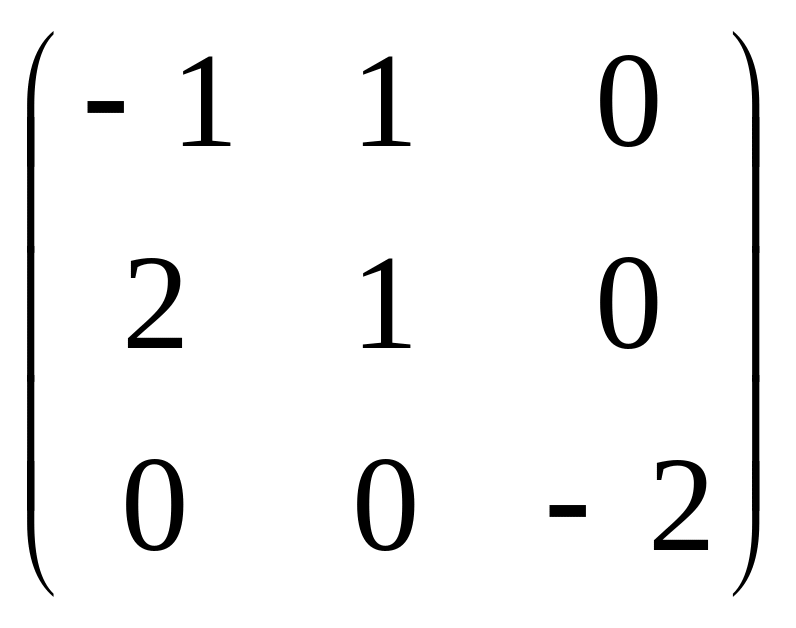 .
50.
.
50.
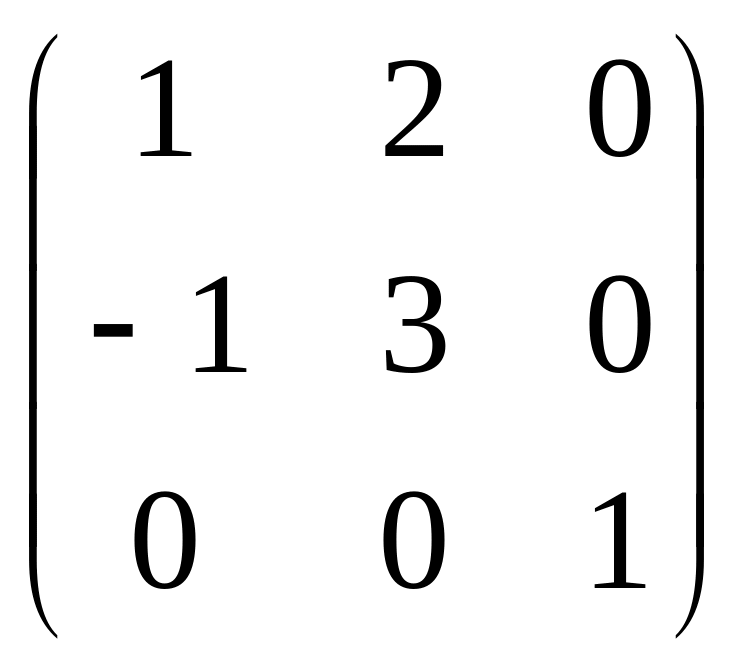 .
.
51.
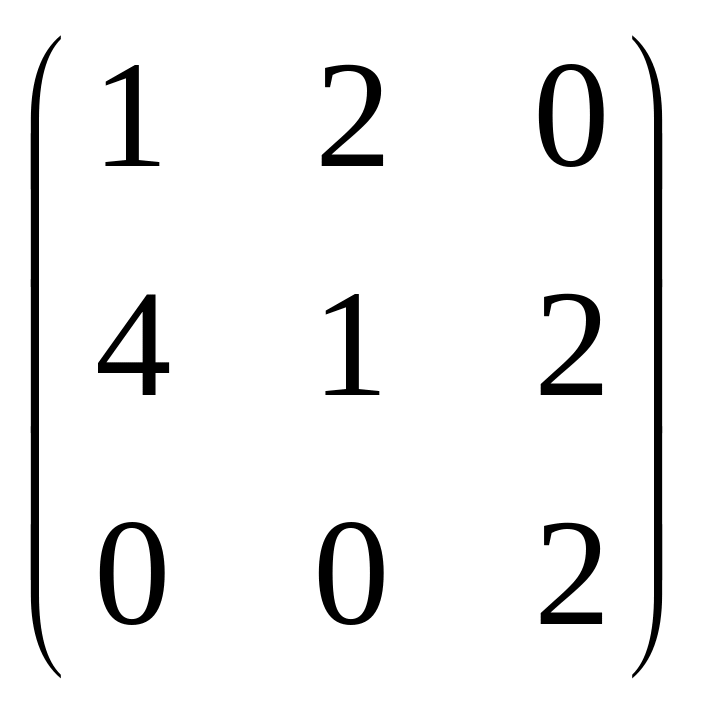 .
52.
.
52.
 .
53.
.
53.
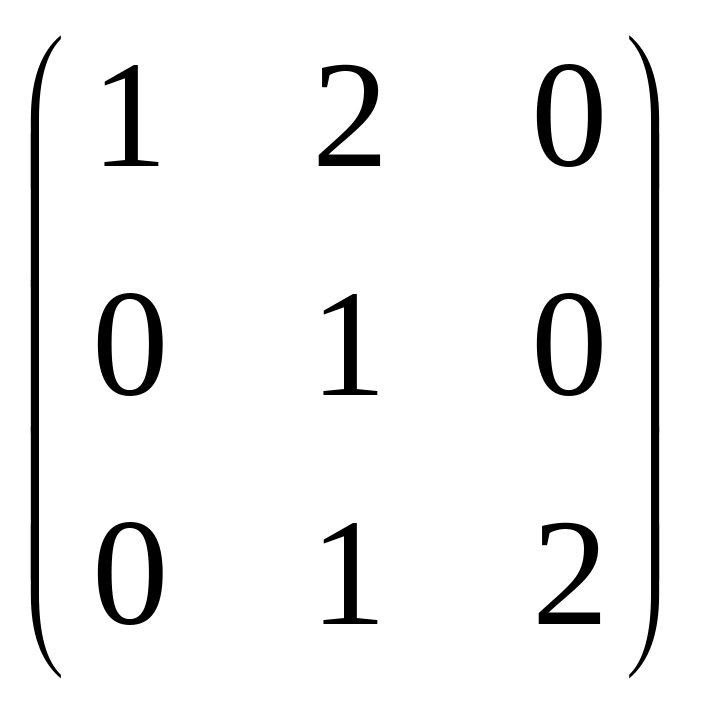 .
54.
.
54.
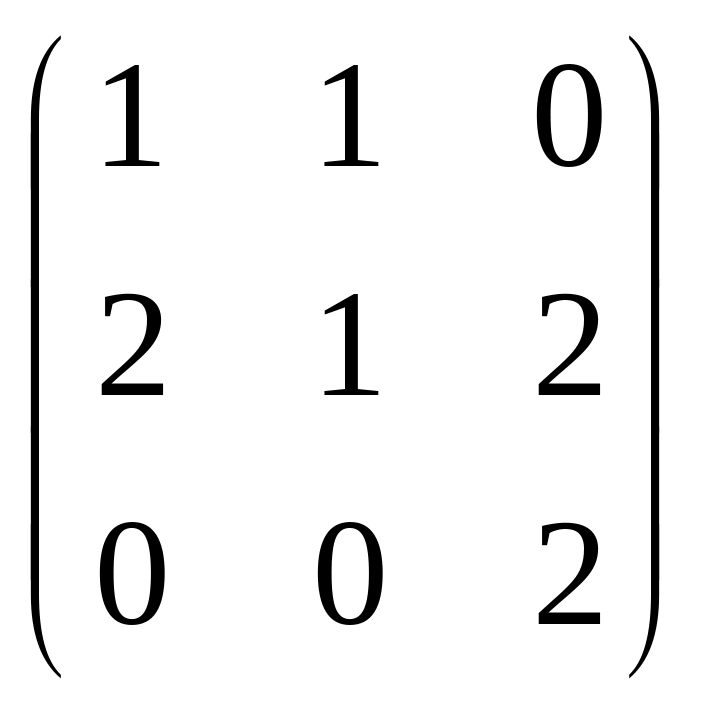 .
55.
.
55.
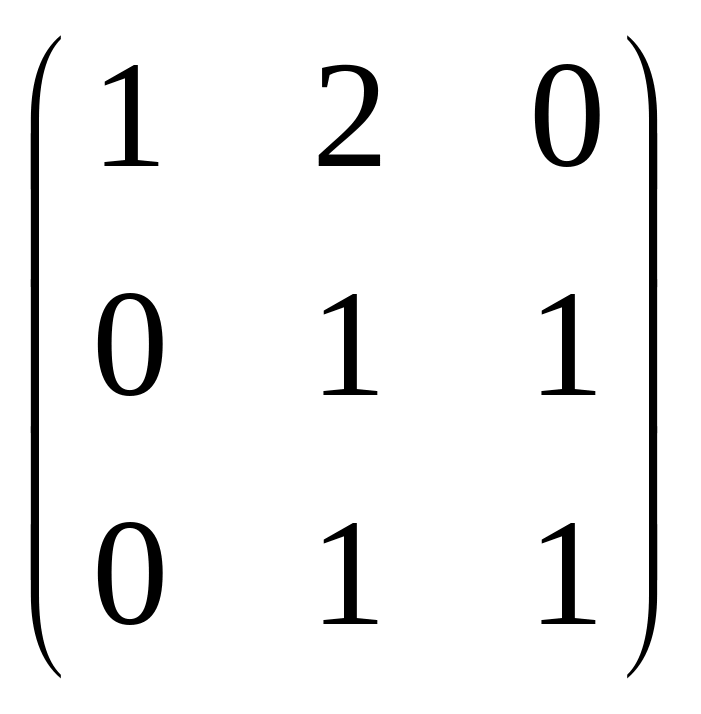 .
.
56.
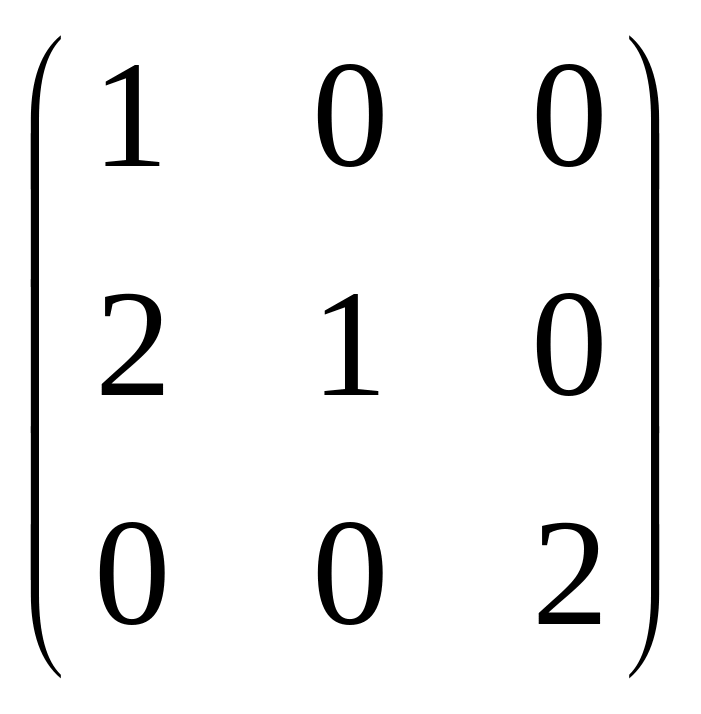 .
57.
.
57.
 .
58.
.
59.
.
58.
.
59.
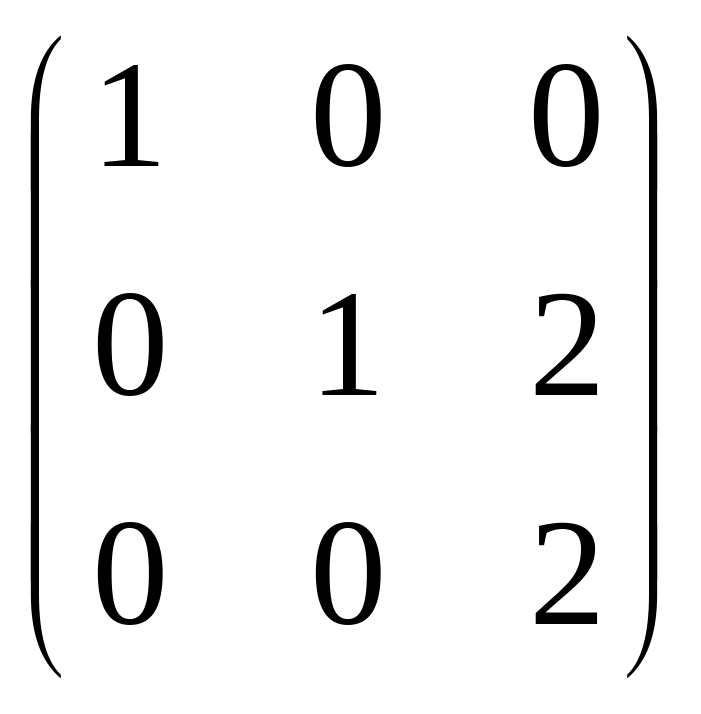 .
60.
.
60.
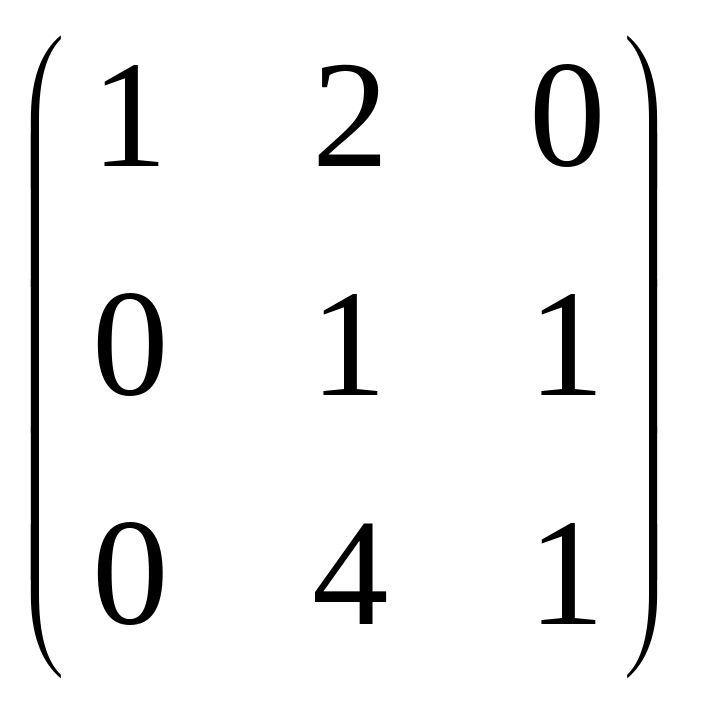 .
.
Для заданной матрицы найти методом итераций наибольшее собственное значение и соответствующий собственный вектор.
61.
 .
62.
.
62.
 .
63.
.
63.
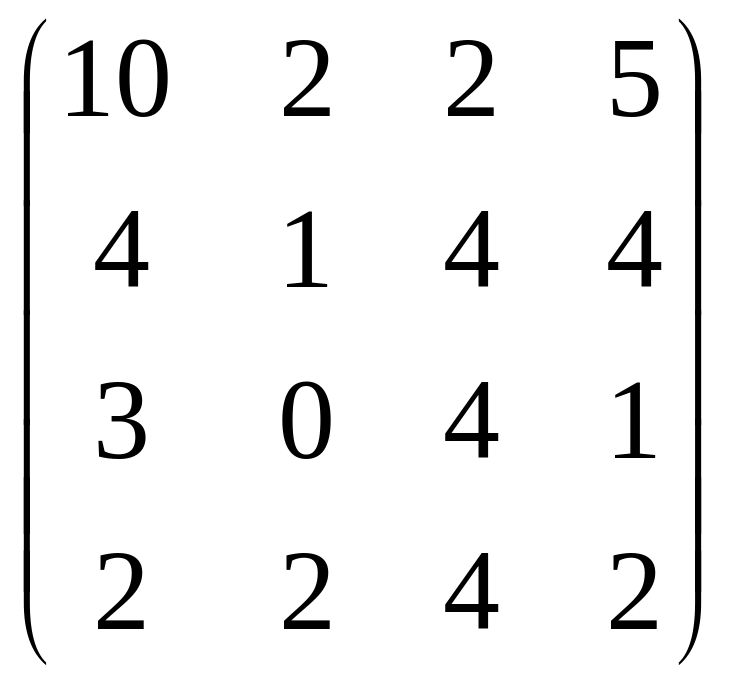 .
64.
.
64.
 .
.
65.
 .
66.
.
66.
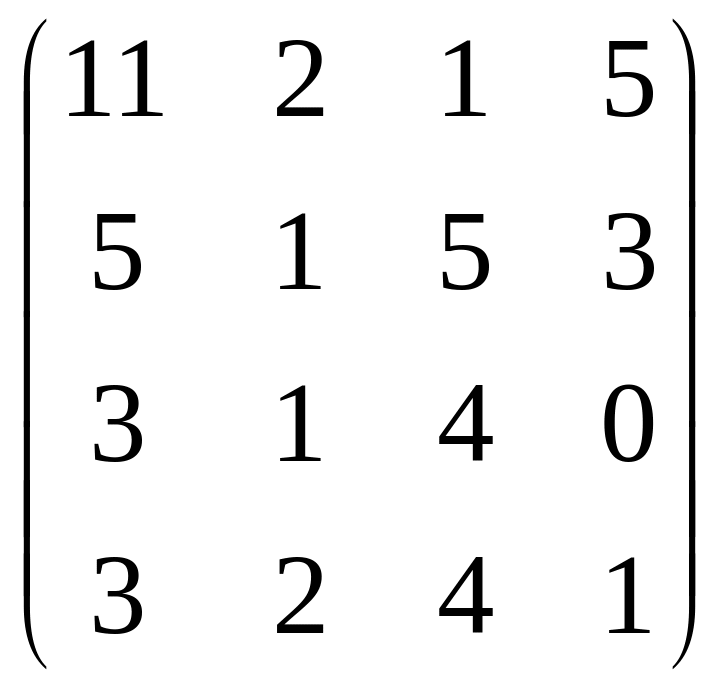 .
67.
.
67.
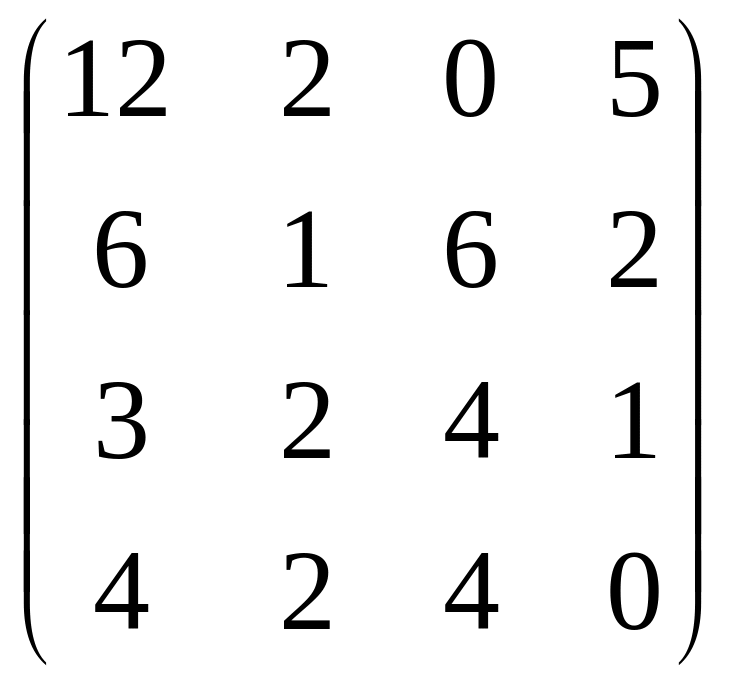 .
68.
.
68.
 .
.
69.
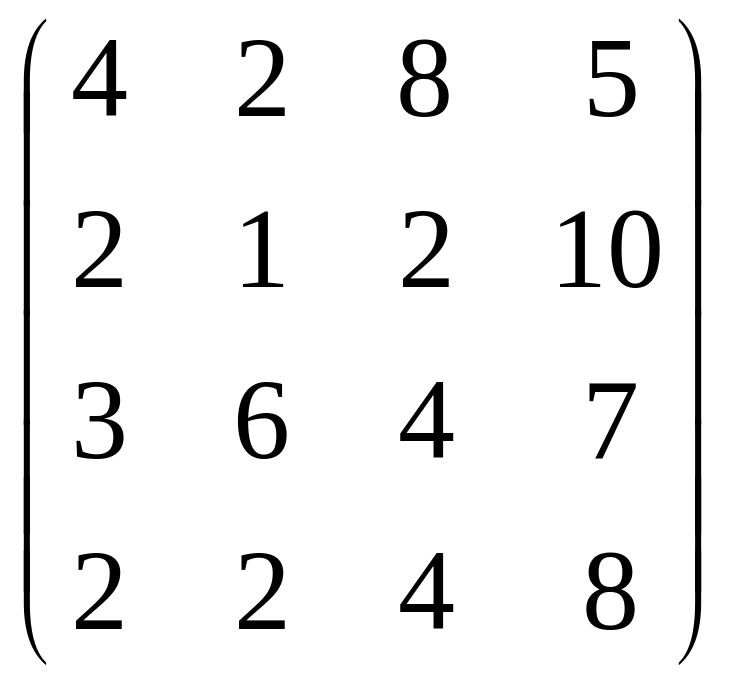 .
70.
.
70.
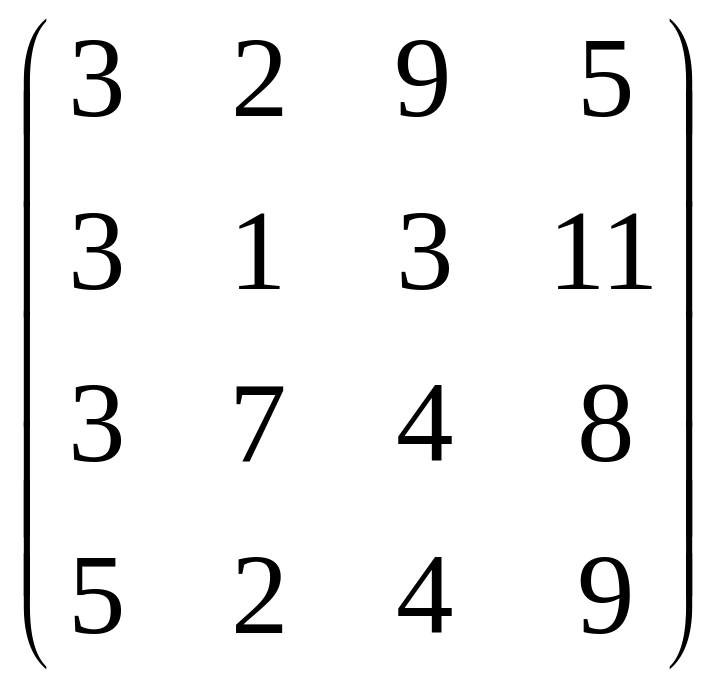 .
71.
.
71.
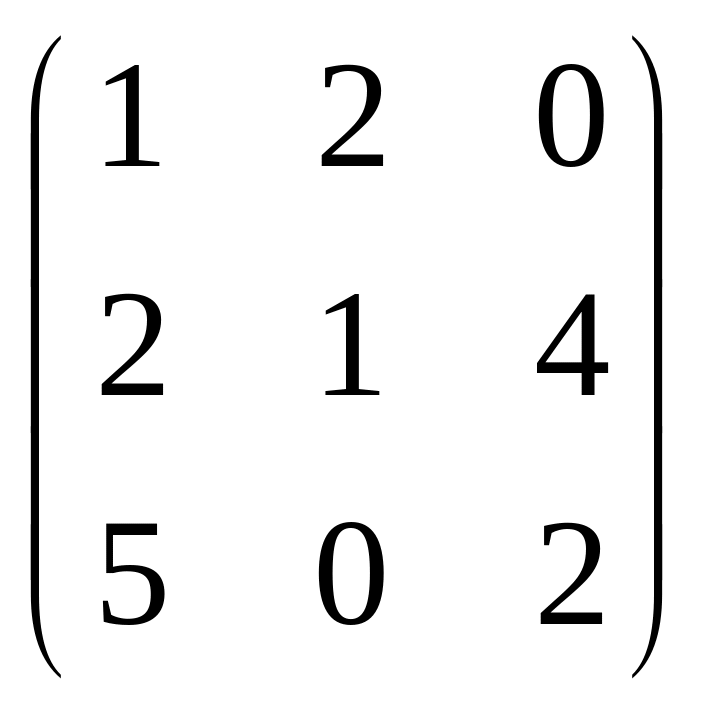 .
72.
.
72.
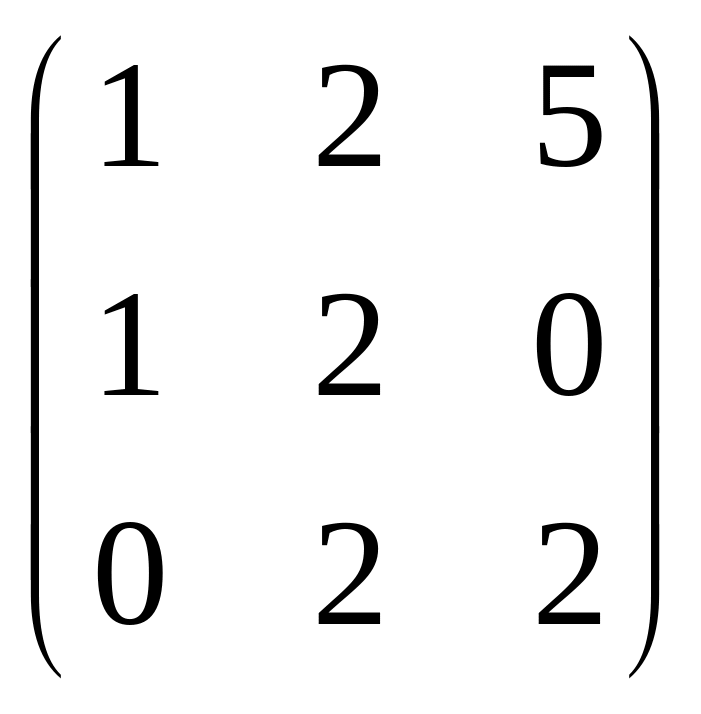 .
73.
.
73.
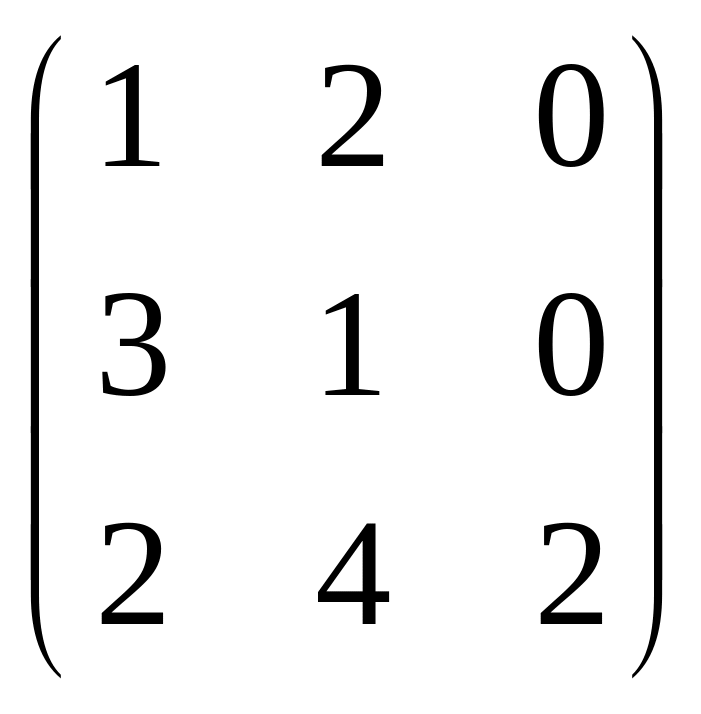 .
74.
.
74.
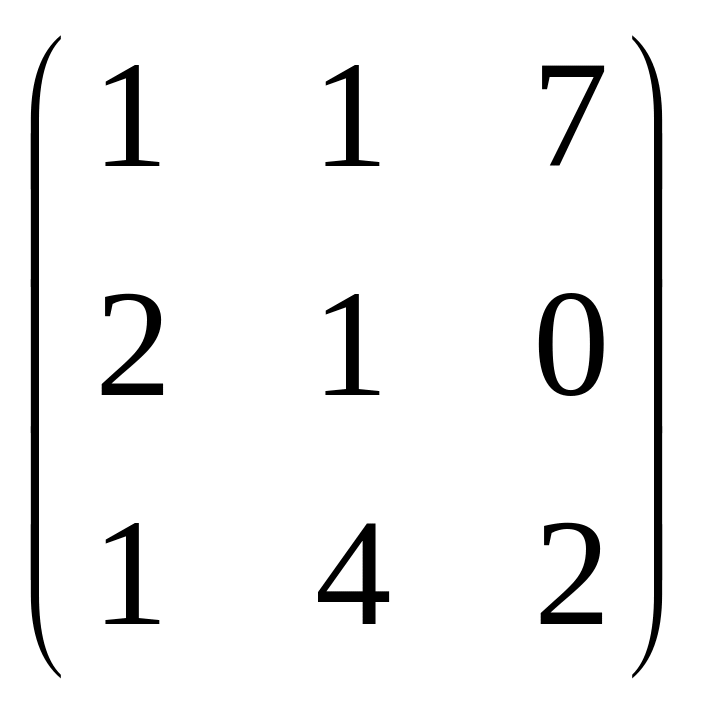 .
75.
.
75.
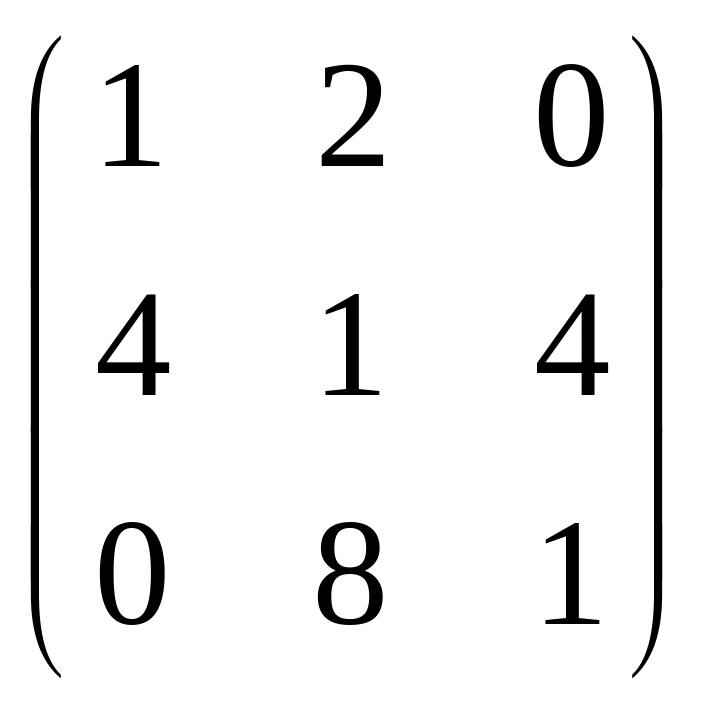 .
76.
.
76.
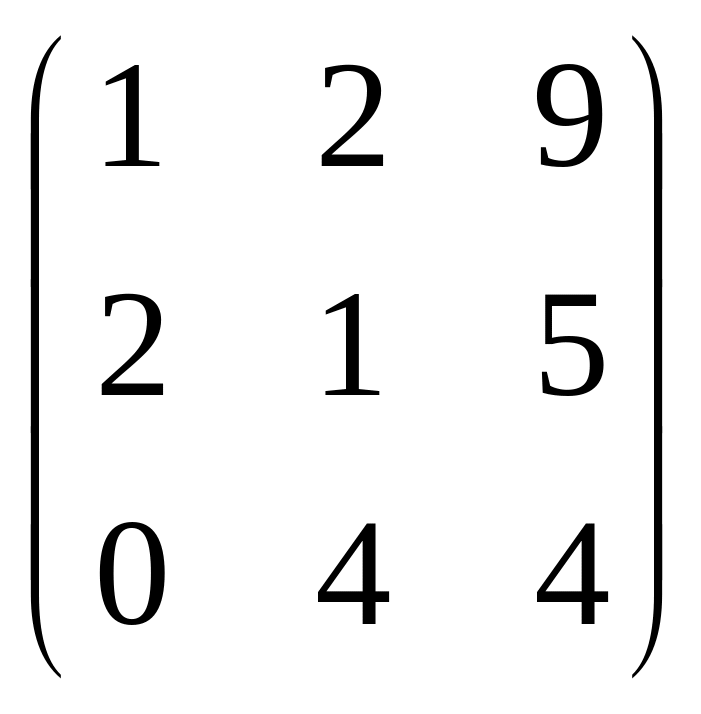 .
77.
.
77.
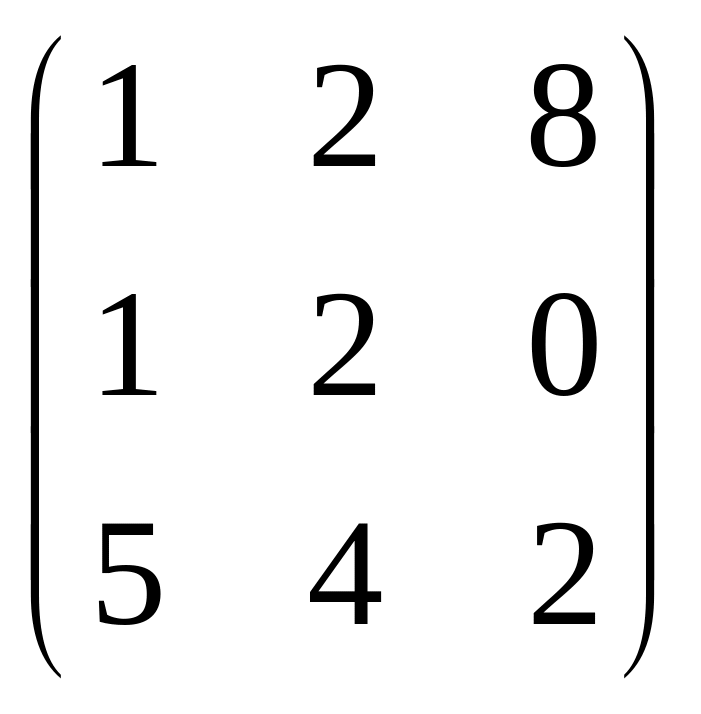 .
78.
.
78.
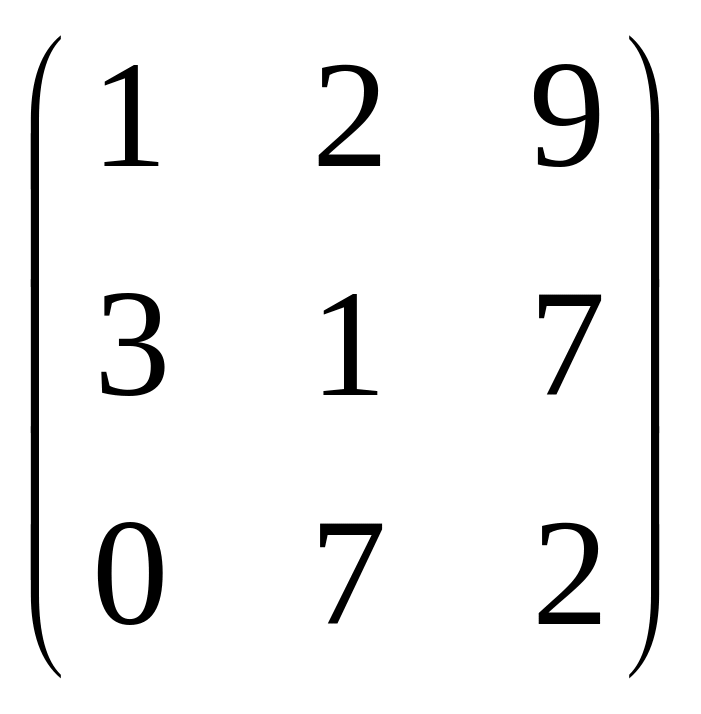 .
79.
.
79.
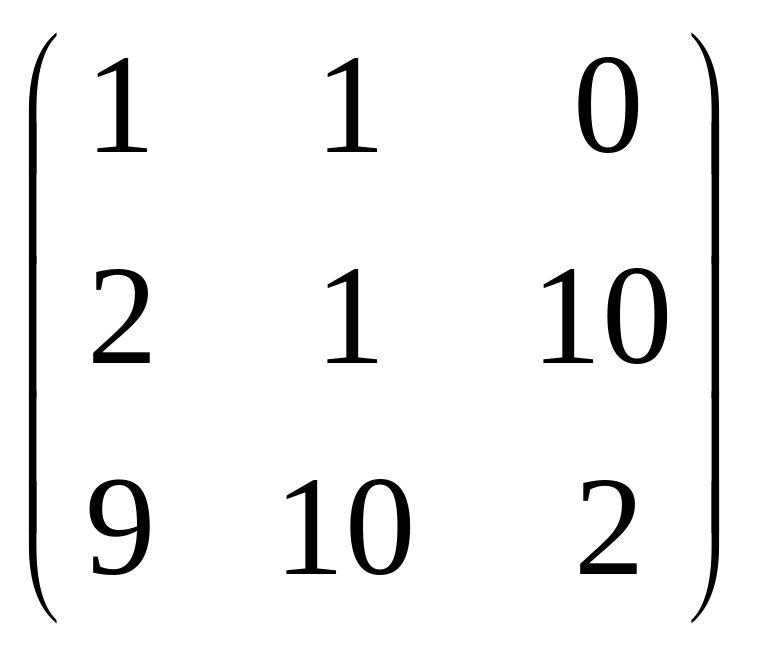 .
80.
.
80.
 .
.
Проверить матрицу на положительную определенность, если матрица положительно определена, найти все собственные значения и собственные векторы.
81. . 82. . 83. . 84. . 85. .
86. . 87. . 88. . 89. . 90. .
91. . 92. . 93. . 94. . 95. .
96. . 97. . 98. . 99. . 100. .
Ответы. (Для номеров 1 — 20 приведены только решения систем уравнений).
1. (0,801; 10,893; –3,678; 0,709), 2. (0,839; –8,345; 5,121; 1,009), 3. (0,858; 6,314; –0,951; 0,230), 4. (1,105; –4,247; 2,880; 1,031), 5. (3,367; –6,905; 4,871; 1,490), 6. (0,909; 4,822; 0,024; –0,466), 7. (0,918; 4,065; 0,300; –1,177), 8. (0,820; 3,250; –0,086; –1,962), 9. (–1,037; 1,899; –1,409; 0,336), 10. (–0,235; 0,862; –0,696; 0,432).
11. (0,922; 10,958; –3,873; 0,886), 12. (1,021; –8,993; 5,39; 1,089),
13. (0,912; 6,271; –1,026; 0,371), 14. (1,207; –4,488; 3,006; 1,061),
15. (0,3; –1,02; 0,94; 0,74), 16. (0,936; 4,787; –0,00495; –0,361),
17. (0,976; 3,984; 0,282; –0,913), 18. (1,024; 3,008; 0,148; –1,123),
19. (0,792; –1,192; 1,083; 0,777), 20. (0,865; –0,84; 0,885; 0,718).
3. Вычислительные методы линейной алгебры 1
3.1. Нормы векторов и матриц 1
3.2. Решение систем линейных алгебраических уравнений 3
3.2.1. Метод Гаусса для решения систем линейных уравнений 4
3.2.2. Итерационный метод 12
3.2.3. Метод Зейделя 16
3.2.4. Погрешность решения и обусловленность системы уравнений 20
3.3. Вычисление определителя и обратной матрицы 23
3.4. Собственные числа и собственные векторы матрицы 29
3.4.1. Метод скалярных произведений 34
3.4.2. Вычисление всех собственных значений положительно определенной симметричной матрицы 35
