
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Утверждено на заседании кафедры
отопления, вентиляции и конди-
ционирования «27» сентября 2007 г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению работы «Аналитические и численные методы решения уравнений математической физики» по дисциплине «Численные методы в системах ОВиК»студентами специальности 290700 «Теплогазоснабжение и вентиляция»
Ростов-на-Дону
2008
Методические указания по выполнению курсовой работы «Аналитические и численные методы решения уравнений математической физики» по дисциплине «Численные методы в системах ОВиК» студентами специальности 290700 «Теплогазоснабжение и вентиляция». –Ростов н/Д: Рост. гос. строит. ун-т, 2008. – 28 с.
Методические указания содержат сведения о численных методах. Рассмотрено решение задач нестационарного температурного поля и двумерно температурного поля.
Составители: канд. техн. наук Н.Н. Руденко,
канд. техн. наук И.Н. Фурсова
Редактор Т.М. Климчук
Темплаш 2008г., поз.225
Подписано в печать 11.05.08. Формат 60х84/16
Бумага писчая. Ризограф. Уч.-изд.л. 2,0.
Тираж 100 экз. Заказ
Редакционно-издательский центр
Ростовского государственного строительного университета
344022, г. Ростов-на-Дону, ул.Социалистическая,162.
© Ростовский государственный
строительный университет, 2008
Введение
Широкое использование математических методов и вычислительной техники открыло новые возможности совершенствования методов прогнозирования и оптимизации инженерных систем зданий. Наиболее актуальным является использование новых методов для оптимизации потребления тепловой энергии и прогнозировании параметров микроклимата в современных зданиях.
Математическая модель
В прикладных задачах исследуется не математический объект, а явления природы, производственный процесс и т.д. Исследование начинается с формализации объекта и построения соответствующей модели. Выделяются наиболее существенные черты и свойства и описываются с помощью математических уравнений. После построения математической модели появляется возможность изучение математическими методами.
Пример. Определить площадь комнаты.
Реальный объект - пол комнаты - заменяют абстрактной моделью – прямоугольником. Ему приписывают размеры, полученные в результате измерений, и площадь такого прямоугольника приближенно принимают за искомую площадь пола.
Соответствие математической модели изучаемому объекту
Математическая модель никогда не бывает тождественна рассматриваемому объекту, не передает всех его свойств и особенностей. Она является его приближенным отражением. Результаты вычислений носят приближенный характер. Точность определяется степенью соответствия, адекватности модели и объекта.
Математические модели позволяют свести исследование реального «нематематического» объекта к решению математической задачи, воспользоваться для его изучения универсальным математическим аппаратом и получить благодаря этому объекту детальную количественную информацию.
Для решения математической задачи важно указать систему правил, которая задает строго определенную последовательность математических операций, приводящих к искомому ответу. Такую систему называют алгоритмом.
В простейших случаях это может быть выражено формулой.
Например, определение площади треугольника. Она равна произведению высоты на половину основания.
Однако существуют алгоритмы, в которых достаточно сложно использовать формулы.
Например, метод нахождения наименьшего частного делителя. Метод основан на последовательно осуществляемом переборе.
Решение уравнения в виде формулы не правило, а скорее исключение.
Метод решения линейных и квадратичных уравнений известен со времен Древней Греции. Решения уравнения третьей и четвертой степени получены только в XV в.
Формулы для решения полинома пятого и более высокого порядка не существует.
При рассмотрении неалгебраического уравнения задача усложняется. Явные выражения для поиска корней становятся исключением.
Пример. Для нахождения корня уравнения используем графический метод. Нанесем на график две кривые, характеризующие правую и левую часть уравнения:
x=cos(x) (1)
Y=X; Y=cos(x)
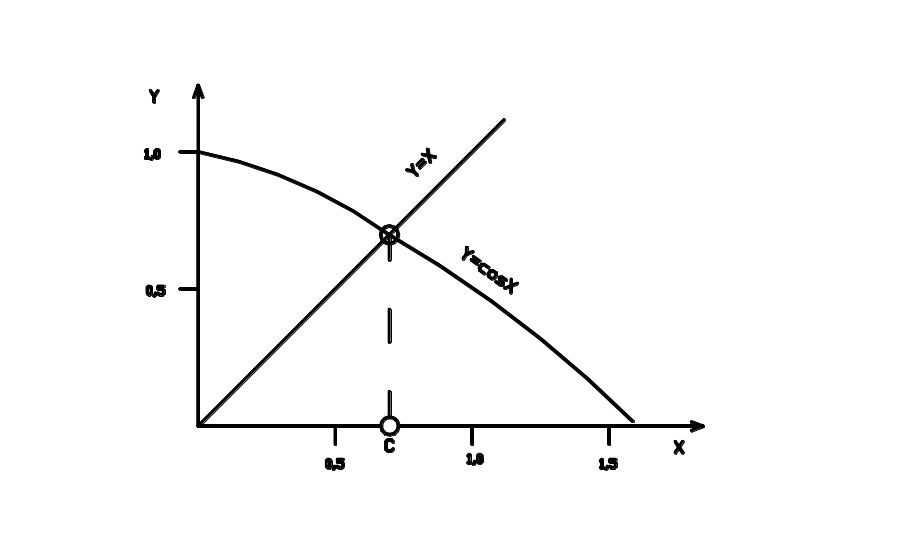 Рис.
1. Графическое решение уравнения x=cos(x)
Рис.
1. Графическое решение уравнения x=cos(x)
Кривые пересекаются на отрезке 0с1; с - корень уравнения, однако получить его по формуле невозможно.
Для определения корня важное значение имеет алгоритм вычисления. Предварительно, как правило, формулу преобразуют и представляют в следующим виде:
f(x) = 0 (2)
Для этой формулы возможно выполнить анализ ее свойств:
непрерывность;
дифференцируемость и др.
