20. Розвиток і сфери застосування методу Монте-Карло

Метод Монте-Карло застосовується в багатьох галузях науки і техніки. Більшість виробничих і соціальних процесів, що характерні для господарських та економічних систем, значною мірою відбуваються під впливом випадкових факторів, які не підлягають контролю з боку осіб, відповідальних за прийняття і реалізацію рішень у контексті забезпечення оптимального функціонування систем.

Зародження методу Монте-Карло пов’язане з дослідженнями фон Неймана та Улана наприкінці 40-х років, коли вони запровадили термін «метод Монте-Карло» і застосували цей метод до розв’язання деяких задач екранування ядерних випромінювань.

Методи Монте-Карло – це загальна назва групи методів для рішення різних задач за допомогою випадкових послідовностей. Ці методи (як і вся теорія імовірностей) виросли з спроб людей поліпшити свої шанси в азартній грі. Цим пояснюється і той факт, що назву цій групі методів дало місто Монте-Карло – столиця європейського грального бізнесу.

Імітаційне моделювання по методу Монте-Карло (Monte-Carlo Simulation) дозволяє побудувати математичну модель для проекту з невизначеними значеннями параметрів, і, знаючи ймовірнісні розподіли параметрів проекту, а також зв'язок між змінами параметрів (кореляцію) отримати розподіл прибутковості проекту.

21. Приклад використання методу Монте-Карло – Задача Бюффона

Кидаємо голку на площину, де зображено рівновіддалені одна від одної паралельні прямі. Яка ймовірність того, що голка перетнеться з однією з прямих ?

Теоретично доведено, що ця ймовірність

Це співвідношення дає змогу експериментально визначити число π. Для цього потрібно, кидаючи голку на площину із зображеними на ній паралельними прямими, фіксувати число m перетинів голки з прямими і число n усіх кидань. Оскільки ймовірність випадкової події оцінюється за частотою появи цієї події, то згідно з цією формулою знайдемо наближене значення:

Це твердження перевірили експериментально. Знайдені результати добре підтвердили відоме значення числа π.

22. Приклад використання методу Монте-Карло – Обчислення визначеного інтеграла

Ідею застосування методу Монте-Карло, зокрема для розв’язання цілком детермінованих задач, легко зрозуміти на прикладі обчислення визначеного інтеграла. Нехай потрібно обчислити інтеграл від деякої функції на заданому відрізку змінювання аргументу. Після нескладних перетворень початкову задачу можна звести до задачі обчислення інтеграла

де 0  f (x)  1 при 0  x  1.

Схему, що ілюструє обчислення визначеного інтеграла методом Монте-Карло, зображено на рис. 6.1.

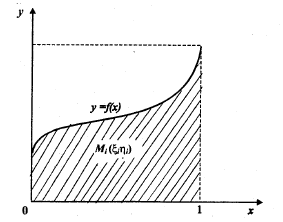
Визначимо площу I фігури, обмеженої кривою y = f (x), віссю x і прямими х = 0, х = 1 (див. рис. 4.3, заштрихована частина).

Уявімо тепер симетричну дзиґу у вигляді десятигранника, кожну з граней якого позначено однією з цифр 0, 1, 2,..., 9. Пустимо дзигу. Після її падіння на верхній грані з однаковою ймовірністю можна очікувати будь-яку з десяти згаданих цифр.

Розглянемо два десяткові k-розрядні числа і , значення яких містяться між нулем та одиницею і утворюються таким чином. Пускаючи k раз дзигу, вважатимемо здобуту послідовність цифр десятковими розрядами числа .