Тема 2.2 нерозгалуджене коло змінного струму

План лекції

2.2.1 Змінний струм в колі з активним опором

2.2.2 Індуктивність у колі синусоїдного струму

2.2.3 Ємність у колі синусоїдного струму

2.2.4 Котушка індуктивності у колі синусоїдної напруги

2.2.5 Послідовне з’єднання R, C

2.2.6 Послідовне з’єднання R, L, C

2.2.1 ЗМІННИЙ СТРУМ В КОЛІ З АКТВНИМ ОПОРОМ

Розглянемо коло з активним опором R (рис. 2.9), яке підключене до джерела синусоїдної наруги:

(2.28)

Рис. 2.9 Коло з активним опором R

Миттєве значення струму визначається за законом Ома:

, (2.29)

де амплітуда струму:

. (2.30)

Рис. 2.10 Хвильова та векторна діаграма для кола з активним опором R

У колі з активним опором R напруга і струм співпадають за фазою (рис. 2.10). Падіння напруги на активному опорі також співпадає за фазою зі струмом:

. (2.31)

2.2.2 Індуктивність в колі синусоїдного струму

Рис. 2.11 Коло з індуктивністю L

Розглянемо ідеальну котушку, у якої R=0. Якщо по котушці протікає змінний струм

, (2.32)

то в ній виникає ЕРС самоіндукції:

. (2.33)

Для того, щоб компенсувати цю ЕРС самоіндукції, необхідно прикласти напругу джерела, яка рівна по величині і протилежна за знаком:

. (2.34)

Виконаємо диференціювання синусоїдного струму і при цьому встановимо фазові співвідношення між напругою і струмом, а також введемо поняття індуктивного опору.

. (2.35)

Замінимо косинусоїду на синусоїду:

(2.36)

Позначимо

(2.37)

і будемо називати його індуктивним опором.

Позначимо і тоді

(2.38)

Порівнявши струм згідно з (2.32) і напругу згідно з (2.38), можна зробити висновок:

у колі з ідеальною індуктивністю напруга випереджає струм на 90⁰, тобто .

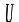
Рис. 2.12 Векторна діаграма струму і напруги для ідеальної котушки

На рис. 2.12 показана векторна діаграма стуму і напруги для ідеальної котушки L. Тут же показана ЕРС самоіндукції Е, що заходиться у протифазі з напругою джерела U.

2.2.3 Ємність у колі синусоїдної напруги

Заряд q та ємність C конденсатора пов’язані співвідношенням:

(2.39)

Рис. 2.13 Коло з ємністю C

Якщо конденсатор підключений до джерела синусоїдної напруги:

, (2.40)

то в колі буде протікати струм:

. (2.41)

Виконаємо диференціювання синусоїдної напруги і при цьому встановимо фазові співвідношення між наругою і струмом, а також введемо поняття ємнісного опору.

(2.42)

Позначимо

(2.43)

і будемо називати його ємнісним опором.

З урахуванням (2.43) струм у колі можна записати:

(2.44)

Позначимо

(2.45)

і тоді

(2.46)

Порівнявши напругу згідно з (2.40) і струм згідно з (2.46), можемо зробити висновок: у колі з ідеальною ємністю струм випереджає напругу на 90⁰, отже .

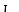
Рис. 2.14 Векторна діаграма струму і напруги для кола з ємністю

На рис. 2.14 показана векторна діаграма струму і напруги для ємнісного кола.

2.2.4 Котушка індуктивності у колі синусоїдної напуги

Реальна котушка індуктивності має активний (R) і індуктивний (X_L) опори.

Рис. 2.15 Коло з реальною котушкою індуктивності

Для схеми на рис. 2.15:

. (2.47)

Тут та – комплекси падінь напруги на активному та індуктивному опорах котушки. Падіння напруги співпадає за фазою зі струмом, а падіння наруги випереджає струм на 90⁰. На основі (2.47) можна побудувати трикутник напруги (рис. 2.16)

Рис. 2.16 Трикутник напруги для реальної котушки індуктивності

Очевидно кут:

. (2.48)

Рис. 2.17 Трикутник опорів для реальної котушки індуктивності (RL– коло)

Якщо всі сторони трикутника напруги розділити на струм І, то отримаємо трикутник опорів (рис. 2.17).

Із прямокутного трикутника опорів за допомогою формул тригонометрії можна отримати необхідні залежності. Так, модуль повного опору Z – це гіпотенуза прямокутного трикутника:

(2.49)

Кут

, (2.50)

(2.51)

(2.52)

Як бачимо із векторної діаграми (рис. 2.16) в RL– колі напруга випереджає струм на кут .

Для реальної котушки індуктивності комплекс опору

(2.53)