1.2.2 Розрахунок розгалуджених кіл методом двох вузлів
Часто зустрічаються схеми, які містять два вузли. У цьому випадку розрахунок струмів віток може бути проведений за методом двох вузлів. Цей метод є окремим випадком методу вузлових потенціалів.
Рис. 1.14 Коло з двома вузлами (вузол b заземлений)
Приймемо
потенціал одного з вузлів за нульовий
(
),
потенціал другого вузла визначають за
формулою:
, (1.32)
де g – провідність вітки. Якщо у вітці включено послідовно декілька опорів, то спочатку необхідної їх додати, а потім визначити провідність вітки. Для кола на рис. 1.14 :
, (1.33)
,
(1.34)
. (1.35)
Напрями
струмів у вітках з ЕРС (активні вітки)
рекомендується направляти за ЕРС, а у
вітках без ЕРС (пасивні вітки) – довільно.
Добуток
береться
зі знаком “плюс” для тієї вітки, у якій
ЕРС направлена до вузла, потенціал якого
визначається
Для
кола на рис. 1.14
має знак “мінус”, а
має знак “плюс”, отже:
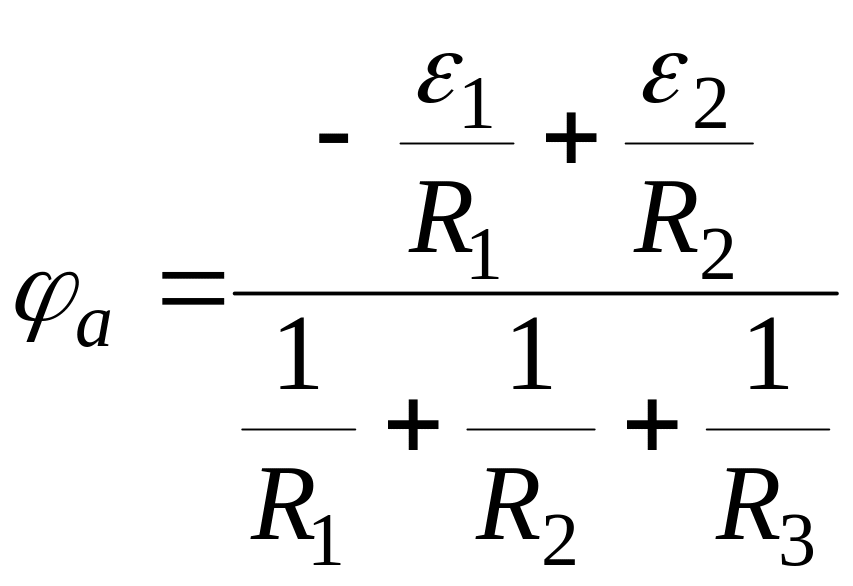. (1.36)
Потім розраховуємо струми віток за узагальненим законом Ома з урахуванням прийнятих умовно додатніх струмів віток:
, (1.37)
,
(1.38)
. (1.39)
Якщо струм у якійсь вітці отримано зі знаком “мінус”, необхідно змінити його напрямок на протилежний. Це необхідно зробити до перевірки балансу потужностей та правил Кірхгофа.
1.2.3 Розрахунок розгалуджених кіл методом правил кірхгофа
Використовуючи закон Ома та правила Кірхгофа можна розрахувати будь-яке коло. Спочатку визначають кількість рівнянь, які необхідно записати за першим та другим правилами Кірхгофа.
Рис. 1.15 Розрахунок складного електричного кола
Приймаємо умовно додатні напрями струмів і показуємо їх на схемі. Як правило у вітках з ЕРС ці струми направляють по ЕРС, а у пасивних вітках – довільно. Бажано, щоб індекс струму і опору даної вітки співпадали. Нехай струми, що входять у вузол b додатні, а струми, що виходять з нього – від’ємні. Для кола на рис. 1.15 за першим правилом складаємо одне рівняння (оскільки коло має два вузли):
. (1.40)
Обираємо напрями обходу контурів і показуємо їх на схемі. Додатніми вважаємо ті ЕРС, напрям яких співпадає з напрямом обходу контуру (зустрічні – від’ємні). Падіння напруги на резисторі додатні, якщо напрям струму в даній вітці співпадає з обходом контуру (від’ємні – якщо на співпадає). За другим правилом для рис. 1.15 складаємо два рівняння (оскільки коло має три контури):
, (1.41)
. (1.42)
Розв’язуючи сумісно рівняння (1.40, 1.41, 1.42) розраховуємо три невідомі струми. Якщо струм у якійсь вітці отримано зі знаком “мінус”, необхідно змінити його напрямок на протилежний.
Питання для самоперевірки знань
1. Закони послідовного з’єднання (малюнок і формули).
2. Закони паралельного з’єднання (малюнок і формули).
3. Опір двох паралельно з’єднаних резисторів (малюнок і формули).
4. Опір трьох паралельно з’єднаних резисторів (малюнок і формули).
5. Опір багатьох паралельно з’єднаних однакових резисторів (малюнок і формули).
6. Перше правило Кірхгофа (сформулювати, скільки рівнянь воно дає, для яких елементів кола).
7. Друге правило Кірхгофа (сформулювати, скільки рівнянь воно дає, для яких елементів кола).
8. Придумати коло з двома вузлами та трьома вітками і застосувати до нього правила Кірхгофа.
9. Перетворення “трикутник – зірка” (придумати схему з “трикутником” і перерахувати її у “зірку”).
10. Перетворення “зірка – трикутник” (придумати схему з “зіркою” і перерахувати її у трикутник”).
11. Придумати вітку з мішаним з’єднанням і визначити її опір.
12. Метод двох вузлів:
а) в яких випадках застосовується;
б) записати формулу для визначення потенціалу ненульового вузла;
в) як визначити струми в вітках?
Теми рефератів
1. Електричні кола в електротехнічних пристроях.
2. Піонери електротехніки.
3. Видатні відкриття і винаходи Г.С. Ома.
4. Видатні відкриття і винаходи Кірхгофа.
5. Техніко-математичні здобутки Гаусса та Крамера.
Питання для самостійного опрацювання
Закони електричних кіл і закони збереження
Метод вузлових потенціалів.