1.8. Понятие о случайном векторе и законе распределения его координат

1.8.1. Примеры случайных векторов

До сих пор мы рассматривали случайные величины, возможные значения которых определялись единственным числом. Такие величины можно назвать одномерными.

Кроме одномерных случайных величин изучают также величины, возможные значения которых определяются двумя, тремя, …, n числами. Такие величины называют двумерными, трехмерными, …, n-мерными случайными величинами или двумерными, трехмерными, …, n-мерными случайными векторами.

Пример 1. Станок-автомат изготавливает втулки длиной Х, наружным Y и внутренним Z диаметрами. Тогда результат контроля деталей есть трехмерная случайная величина (X,Y,Z) (трехмерный случайный вектор с координатами (X,Y,Z)).

Пример 2. Бросаются две игральные кости. Результат испытания можно характеризовать двумерной случайной величиной (Х₁,Х₂), где Х_i – число очков, выпавшее на i-й кости (i=1, 2).

Мы в дальнейшем ограничимся рассмотрением двумерных случайных величин, как в свое время ограничились рассмотрением функций двух переменных. Принципиальных трудностей для рассмотрения случайных величин большей размерности нет, хотя их описание и соответствующий математический аппарат, естественно, усложняются.

1.8.2. Закон распределения и функция распределения двумерной случайной величины

Законом распределения дискретной случайной величины называют перечень ее возможных значений, т.е. пар чисел (х_i, y_j) и их вероятностей р_ij (i=1, …, n; j=1, …, m). Обычно закон распределения задают таблицей с двумя входами:

Х Y	x1	x2	…	xn
y1	p11	p12	…	p1n
y2	p21	p22	…	p2n
…	…	…	…	…
ym	pm1	pm2	…	pmn

Все события в таблице несовместны и образуют полную группу, поэтому

. (1.8.1)

Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих. В самом деле, чему, например, равна вероятность того, что Х=х₁? Если Х=х₁, то Y при этом может принять любое из своих возможных значений у₁, …, у_m. Это значит, что вероятность того, что Х=х₁ равна вероятности наступления одного из событий: (х₁, у₁), (х₁, у₂), …, (х₁, у_m). Но эти события несовместны, поэтому по теореме сложения вероятностей:

.

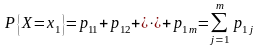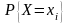Таким образом, вероятность равна сумме вероятностей, находящихся в первом столбце. В общем случае, чтобы вычислить вероятность , надо просуммировать все вероятности в i-м столбце таблицы. Аналогично, сложив все вероятности

в j-й строке, получим вероятность .

Пример. Найти законы распределения составляющих двумерной случайной величины, заданной законом распределения:

Х Y	x1	x2	х3
y1	0,1	0,3	0,2
y2	0,06	0,18	0,16

Решение. Сложив вероятности по столбцам, получим вероятности возможных значений Х:

P{X=x₁}=0,1+0,06=0,16;

P{X=x₂}=0,3+0,18=0,48;

P{X=x₃}=0,2+0,16=0,36.

Закон распределения случайной величины Х:

Х	х1	х2	х3
Р	0,16	0,48	0,36

Аналогично, складывая вероятности по строкам исходной таблицы, получим:

P{Y=y₁}=0,1+0,3+0,2=0,6;

P{Y=y₂}=0,06+0,18+0,16=0,4.

Закон распределения случайной величины Y:

Y	y1	y2
Р	0,6	0,4