1.2.2. Биномиальное распределение

Рассмотрим схему Бернулли: нас интересует последовательность n независимых испытаний, в каждом из которых с одинаковой вероятностью р может произойти событие А. Рассмотрим случайную величину Х – число появлений события А в этой серии испытаний. Наша задача – найти закон распределения величины Х. Для этого мы должны ответить на два вопроса: 1) каково множество возможных значений Х? и 2) каковы их вероятности?

Очевидно, х₁=0, х₂=1, …, х_n+1=n, т.е. величина Х может принимать дискретные значения 0, 1, …, n. На второй вопрос ответ дает формула Бернулли:

Р_n(m)= p^mq^n–m, (1.2.2.1)

где m=0, 1, …, n.

Формула (1.2.2.1) и является аналитическим выражением, определяющим закон распределения. Этот закон носит название биномиального закона распределения. Название связано с формулой бинома Ньютона:

.

Биномиальный закон можно изобразить и в виде таблицы:

Х	N	n–1	…	m	…	0
Р	pn	npn–1q	…	pmqn–m	…	qn

Пример. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины Х – числа выпадений герба.

Решение. Вероятность появления герба в одном бросании , вероятность того, что герб не появится, 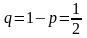. При двух бросаниях герб может появиться либо 0, либо 1, либо 2 раза.

Вероятности этих значений подсчитаем по формуле Бернулли:

Р₁=Р₂(0)=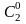 q²=q²= ,

P₂=P₂(1)=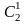 pq=2 ,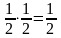

P₃=P₂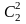(2)= p²=p²= .

Как и следовало ожидать, Р₁+Р₂+Р₃=1. Таблица закона распределения имеет вид:

Х	0	1	2
Р	0,25	0,5	0,25

1.2.3. Распределение Пуассона (пуассоновское приближение биномиального распределения)

Еще раз обратимся к схеме n независимых испытаний, в каждом из которых вероятность появления события А равна р, а вероятность события равна q=1–p. В общем случае для определения вероятности m появлений события А справедлива формула Бернулли. Если n велико (n50), то для расчетов справедлива асимптотическая формула Лапласа. Однако эта асимптотическая формула дает плохие результаты, если вероятность р мала (р0,1), т.е. в ситуации, когда изучаются довольно "редкие" события.

В области n, p0 существует еще одна асимптотическая формула, которая носит название формулы Пуассона или распределения Пуассона. Она выводится в предположении, что при n и р0 величина =np является константой.

Распределение Пуассона имеет вид:

, m=0, 1, 2, … . (1.2.3.1)

Им обычно пользуются вместо биномиального в ситуации, когда n>>1, а р<<1. Имеются специальные таблицы распределения Пуассона, которые позволяют по известным n и m найти Р_n(m).

Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что при перевозке изделие повредится, равна 0,0002. Найти вероятность того, что на базу привезут 3 негодных изделия.

Решение. n=5000; p=0,0002; m=3. Сначала найдем =np=50000,0002=1. По формуле Пуассона

Р₅₀₀₀(3)=