2.1. Постановка задачи линейного программирования.

Математическая модель задачи – это отражение оригинала в виде функций, уравнений, неравенств, цифр и т.д.

Задача линейного программирования соответствует частному случаю общей модели, когда соотношение, описывающее критерий эффективности и пространство стратегий линейны по контролируемым переменным – стратегиям.

Любая задача линейного программирования включает:

1. Целевую функцию (линейную форму), максимум или минимум (оптимум) которой требуется найти.

2. Ограничения в виде системы линейных уравнений (неравенств).

3. Требование не отрицательности переменных.

Стандартная формулировка общей задачи линейного программирования выглядит так: требуется найти экстремальное значение показателя эффективности (целевой функции)

(1.9)

при линейных ограничительных условиях, накладываемых на элементы решения:

(1.10)

………………………………………

, (1.11)

где а_ij, b_i, c_j — заданные числа.

Условие (1.11) необязательно, но его всегда при необходи­мости можно добиться. Обозначение { говорит о том, что в конкретном ограничении возможен один из знаков: или .

Формы записи задач линейного программирования

Общей формой записи задачи линейного программирования называют задачу максимизации или минимизации линейной функции

f = max (min) (2.1.)

при линейных ограничениях

и при условиях

,

, , (2.3.)

где J₁ J₂ =( j= ) и а_ij, b_i, c_j — постоянные числа.

Симметричной формой записи задачи линейного программирования называют задачу максимизации линейной функции (2.1.), при линейных ограничениях (2.2.), когда все ограничения имеют смысл неравенства вида «≤» и все переменные неотрицательны, т.е.

f = max (2.4.)

(2.5.)

(2.6.)

Канонической формой записи задачи линейного программирования называют задачу максимизации линейной функции (2.1.), при линейных ограничениях (2.2.), когда все ограничения имеют смысл равенства и все переменные неотрицательны, т.е.

f = max (2.7.)

(2.8.)

(2.9.)

На практике часто приходится одну форму записи задачи линейного программирования преобразовывать в другую. При этом пользуются следующими соображениями:

1. При необходимости задачу максимизации можно заменить задачей минимизации и наоборот. Экстремум этих функций достигается в одной и той же точке, т.е. min f = - max ( -f ). После решения задачи max ( -f ) необходимо изменить на противоположный знак оптимума функции.

2. Если на какую-либо переменную не наложено условие неотрицательности (например х_к), то её можно заменить разностью двух новых неотрицательных переменных (х_к’ и x_к’’), т.е. х_к=х_к’–x_к’’.

3. Любое ограничение неравенство задачи линейной оптимизации вида “ ”, можно преобразовать в равенство добавлением к его левой части дополнительной неотрицательной переменной, а неравенство, вида “ ” ― вычитанием из его левой части дополнительной неотрицательной переменной.

В экономических задачах дополнительные переменные всегда имеют определенный, практический смысл.

Известно, что система "m" уравнений с "n" переменными может быть как совместной, так и несовместной, а уравнения системы как зависимыми, так и независимыми. В дальнейшем условимся, что все "m" уравнений системы линейно не зависимы. Совместная система "m" уравнений с "n" неизвестными имеет бесконечное множество всевозможных решений.

Для поиска оптимального решения среди бесчисленного множества допустимых решений существует много методов, которые будут здесь изложены. В основу поиска оптимального решения задачи линейного программирования, положены некоторые теоремы. Приведем формулировки этих теорем без доказательств, но справедливость их покажем на примерах.

Основные теоремы линейного программирования

Теорема 1. Множество всех допустимых решений, системы ограничений задачи линейного программирования, является выпуклым.

Теорема 2. Если задача линейного программирования имеет оптимальное решение, то оно совпадает с одной (двумя) из угловых точек множества допустимых решений.

Пример. Найти максимум функции

F=X₁-X₂

п ри ограничениях:

3X₁+2X₂<=14

X₁-4X₂<=0

3X₁-X₂>=0

-X₁+X₂<=2

X₁,X₂>=0

Найдём оптимальное решение поставленной задачи геометрическим способом. Для этого в системе координат Х₁,Х₂ построим множество допустимых решений, используя систему неравенств. Убедимся в справедливости теоремы 1. На рисунке 1 множество допустимых решений пред­ставляет собой замкнутый выпуклый четырехугольник с вершинами О D, В,С. Функция "F" может принимать различные значения из области допустимых значений, т.е. Х₁-Х₂=а

Меняя величину "а", получим семейство параллельных прямых. Теорема 2. утверждает, что максимум или минимум функции F достигается в одной из вершин области допустимых решений. Убедимся в этом, последовательно подставляя координаты вершин в выражение целевой функции F. Максимум будет в точке С с координатами X₁=4, Х₂=1 и значение его равно 3 (4-1=3).

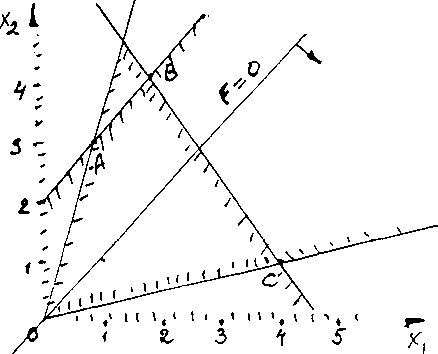
Рис. 2.1.

Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка, области допустимых решений системы ограничений и наоборот.

Вернемся к задаче. Систему ограничений сведем к системе уравнений, добавив в левую часть неравенств дополнительные переменные.

З Х₁+2Х₂+Х₃=14

X₁-4X₂+X₄=0

-3X₁+X₂+X₅=0

-X₁+X₂+X₆=2

Система четырех независимых уравнений с шестью переменными имеет множество решении. Найдем некоторые базисные решения.

1. Положим Х₁=Х₂=0. Подставляя эти значения в систему уравнений, получим базисное решение (0,0,14,0,0,2).Оно допустимо, т.к. Х₁, Х₂, Х₃, Х₄, Х₅, Х₆ больше нуля и вырождено, т.к. Х₄=Х₅=0.

2. Найдем теперь второе базисное решение, полагая X₁=X₆=0. Подставим эти значения в систему уравнений и, решая эту систему относительно оставшихся неизвестных переменных, получим второе базисное решение (0,2,10,8,-2,0).Оно не допустимо, т.к. Х₅=-2 отрицательно.

3. Третье базисное решение получим аналогичным способом, полагая Х₃=Х₄=0. Базисное решение (4,1,0,0,11,5) допустимо и соответствует решению, полученному геометрическим способом (вершина С).

Таким же образом можно найти все базисные решения, выбрать среди них допустимые, подставляя значения X₁ и Х₂ в целевую функцию, получить значения функции и среди этих значений выбрать максимальное. Очевидно, что для данной задачи число базисных решений будет равно числу сочетаний из шести по четыре, а именно: С⁴₆=15. В общем случае количество базисных решений равно

C^mn=n!/m!(n-m)! (2.3)

Замечание. Если в угловой точке соответствуют два, три и более базисных решений, то все они будут вырожденными.

Следствие из теоремы 1 и теоремы 2 оптимальное решение задачи линейного программирования, заданной ограничениями - уравнениями совпадает с допустимым базисным решением системы ограничений.

Замечание. Если система ограничений задачи линейного программирования задана в виде системы линейных неравенств, с двумя переменными или число переменных превышает число уравнений на два, то такая задача может быть решена геометрически.

Что Вы должны знать:

(вопросы для самоконтроля)

1. Из чего состоит задача линейного программирования?

2. Какие параметры являются заданными в задаче линейного программирования, и какие надо найти?

3. Какова формулировка первой теоремы линейного программирования?

4. Какое решение является допустимым решением задачи линейного программирования?

5. Что позволяет определить вторая теорема линейного программирования?

6. Какие задачи линейного программирования решаются геометрическим способом?

7. В каком случае оптимальное решение не является единственным?

8. В каких случаях задача линейного программирования не имеет решения, решение стремится к бесконечности?