2.3.2. Сетевое планирование и управление
Сетевое планирование и управление основано на моделировании процесса с помощью сетевого графика и представляет собой совокупность расчетных методов, организационных и контрольных мероприятий по планированию и управлению комплексом работ.
2.3.3. Основные понятия и терминология, используемые в сетевом планировании
Комплекс работ - это задача, для выполнения которой необходимо осуществить достаточно большое количество разнообразных работ.
Сетевая модель - это план выполнения некоторого комплекса взаимосвязанных работ, заданного в форме сети, графическое изображение которой называется сетевым графиком.
Главными элементами сети являются события и работы.
Работа может быть определена как действительная работа, т. е. протяженный во времени процесс с затратами ресурсов, либо -это ожидание, т.е. протяженный во времени процесс, не требующий затрат труда, либо -это фиктивная работа, не требующая времени и затрат ресурсов. Фиктивная работа указывает, что возможность выполнения одной работы непосредственно зависит от результатов другой.
Событие - это момент завершения какого- либо процесса. Последующие работы могут начаться только тогда, когда событие завершиться. Отсюда следует двойственный характер события. С одной стороны - это конечное событие для одной работы, с другой стороны - это начальное событие для следующей. Событие не имеет протяженности во времени. Среди событий есть исходное (первое) и завершающее (последнее). В сетевых графиках событие обычно изображают кружочками, а работы стрелками.
Рис.2.3.
2.3.4. Порядок построения сетевых графиков
1. Планируемый процесс разбивается на отдельные работы.
2. Составляется перечень работ и событий.
3. Продумываются их логические связи и последовательность выполнения.
4.Оценивается длительность каждой работы.
5. Составляется сетевой график..
6. Рассчитываются параметры событии к работ.
7.Определяются резервы времени для событий и работ.
Проводится анализ и оптимизация сетевого графика.
2.3.5. Правила построения сетевого графика.
При построении сетевого графика необходимо соблюдать ряд правил.
В сетевой модели не должно быть "тупиковых" событий, т.е. событий, из которых не выходит ни одна работа, за исключением завершающего события.
2
.
В сетевом графике не должно быть
"хвостовых" событий (кроме
исходного), которым не предшествует
хотя бы одна работа.
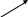
Рис.2.4.
3. В сети не должно быть замкнутых контуров и петель, т.е. путей, соединяющих некоторые события с ними же самими.
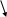
Рис. 2.5.
4. Любые два события должны быть непосредственно связаны не более чем одной работой стрелкой.
5. В сети рекомендуется иметь одно исходное и одно завершающее событие.
Если в соответственной сети это не так, то добиться желаемого можно путём введения фиктивных событий и работ.
2.3.6. Основные понятия сетевого графика
Путь – это любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы.
Полный путь – это любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.
Критический путь – наиболее продолжительный путь. Критическими называют также работы и события, расположенные на этом пути.