
- •Введение
- •1.Основные понятия и принципы моделирования Определение моделирования
- •1.1. Принципы построения математических моделей
- •Обобщенная математическая модель
- •1.2. Оценка эффективности стратегий
- •1.3. Классификация задач исследования операций
- •1.4. Модели выбора решений в условиях определенности
- •2. Математическое программирование
- •2.1. Постановка задачи линейного программирования.
- •Формы записи задач линейного программирования
- •Решение задачи лп графическим методом :
- •Геометрическая интерпретация и графический метод решения задачи линейного программирования
- •3. Геометрическая интерпретация задач линейного программирования
- •2.1.1 Симплексный метод решения задач линейного программирования
- •2.1.2Алгоритм симплекс метода отыскания оптимального решения задачи линейного программирования
- •2.1.3Примеры решения задач симплексным методом Пример 1. Найти максимум целевой функции
- •§4. Решение задачи лп двухфазным симплекс-методом
- •2.1.4 Задачи для закрепления полученных знаний
- •2.1.5. Двойственная задача
- •2.1.6Основные теоремы двойственности
- •2.1.7. Транспортная задача
- •2.1.8. Первоначальное распределение поставок
- •2.1.9. Правило "Северо-западного угла"
- •2.1.11. Метод потенциалов.
- •2.2. Модели динамического программирования
- •2.2.1. Постановка задачи динамического программирования
- •2.2.2. Принцип оптимальности и математическое описание динамического процесса управления
- •2.2.3. Оптимальное распределение инвестиций
- •2.2.3. Выбор оптимальной стратегии обновления оборудования
- •2.3. Сетевое моделирование. Методы и модели теории графов и сетевого моделирования
- •2.3.1. Элементы теории графов
- •2.3.2. Сетевое планирование и управление
- •2.3.3. Основные понятия и терминология, используемые в сетевом планировании
- •2.3.4. Порядок построения сетевых графиков
- •2.3.5. Правила построения сетевого графика.
- •2.3.6. Основные понятия сетевого графика
- •2.3.7. Временные параметры сетевых графиков
- •3. Задачи в условиях неопределенности
- •3.1. Системы массового обслуживания
- •3.1.1. Структура простейшей системы массового обслуживания.
- •3.1.2. Система массового обслуживания с отказом. Одноканальная система.
- •3.1.3. Системы массового обслуживания с ожиданием.
- •Имитационное моделирование
- •3.2.1. Основы имитационного моделирования
- •3.2.2. Метод статистических испытаний
- •3.2.3. Формирование случайных чисел на эвм
- •3.3. Модели прогнозирования. Задачи управления запасами
- •3.3.1.Основные понятия управления запасами
- •3.3.2. Классификация моделей управления запасами
- •3.3.3. Складская система
- •3.3.4. Спрос на товары
- •3.3.5. Возможность пополнения запасов
- •3.3.6. Затраты на функционирование системы управления запасами
- •3.3.7. Стратегия управления запасами
- •3.3.8. Основные детерминированные модели. Простейшая модель управления запасами ( модель 1)
- •3.3.9. Модель с учетом дефицита (модель 2)
- •С помощью этих соотношений исключим т1, т2, т и получим
- •Оптимальное значение
- •График зависимости уровня запаса на складе от времени
- •Методы и модели теории игр
- •3.4.1. Основные понятия теории игр
- •3.4.2. Постановка игровых задач
- •3.4.3. Методы решения игровых задач
- •3.4.4. Метод линейного программирования
- •Литература
2.1.6Основные теоремы двойственности
Теорема 1.
Если задача линейного программирования имеет конечный оптимум, то двойственная к ней также имеет конечный оптимум, и оптимальные значения линейных форм обеих задач совпадают, т.е.
Fmax=Zmin или Fmin=Zmax
Замечание.
Если линейная форма одной из двойственных задач не ограничена, то условия другой задачи противоречивы.
Теорема 2.
Компоненты оптимального решения задачи линейного программирования равны абсолютным значениям коэффициентов при соответствующих переменных в выражении линейной формы двойственной ей задачи при достижении ею оптимума.
Замечание.
Если в одной из задач (прямой или двойственной) нарушается единственность оптимального решения, то оптимальное решение другой задачи будет вырожденным.
Из теорем 1 и 2 следует вывод, что, решив одну из взаимно двойственных задач, т.е. найдя её оптимальное решение и оптимум линейной формы, мы можем записать оптимальное решение оптимум линейной формы другой задачи.
Соответствие между переменными исходной и двойственной задачи:
X1 X2 ...Xn Xn+1 Xn+2 ...Xn+m
| | | | | |
Ym+1 Ym+2 ...Ym+n Y1 Y2 ...Ym
Теорема об оценках, экономическая интерпретация двойственной задачи.
Значения переменных Yi в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов Bi системы ограничений исходной задачи на величину Fmax,т.е.
Yi=dFmax/dBi (2.10)
Эта теорема показывает ещё одну связь между прямой и двойственной задачами.
Пусть (X1,X2...Xn)-оптимальное решение исходной задачи, а (Y1,Y2...Yn)-оптимальное решение двойственной задачи.
Оптимальные значения целевых функций F и Z достигаются при подстановке компонент оптимального решения в их первоначальные выражения,т.е.
Fmax=C1X1+C2X2+...+CnXn (2.11)
Zmin=B1Y1+B2Y2+...+BmYm (2.12)
На основании первой теоремы двойственности (Fmax=Zmin) можно записать:
C1X1+C2X2+...+CnXn=B1Y1+B2Y2+...+BmYm (2.13)
Отсюда следует, что
Fmax=B1Y1+B2Y2+...+BmYm (2.14)
Посмотрим, как изменится величина Fmax, если в исходной задаче увеличить свободный член Bi на величину ΔBi.
Величина Fmax, рассматриваемая теперь как функция переменных B1,B2,...Bm, получит приращение ΔFmax. Продифференцируем функцию Fmax по переменным Bi и найдем дFmax.
дFmax=YiдBi (2.15)
Учитывая, что функция Fmax линейная, получим:
в конечных приращениях
ΔFmax=YiΔBi (2.16)
Приращение максимума целевой функции пропорционально приращению свободного члена с коэффициентом влияния равным соответствующему значению переменной двойственной задачи.
первое
свойство двойственных оценок:
двойственные оценки уi
(i =
![]() ),
— являются инструментом балансирования
затрат и результатов.
),
— являются инструментом балансирования
затрат и результатов.
Рассмотрим следствие, вытекающее из первой теоремы, которое представлено в виде второй теоремы двойственности.
Теорема 2 (о дополняющей нежесткости).
-
Для того, чтобы планы
 *
и
*
и
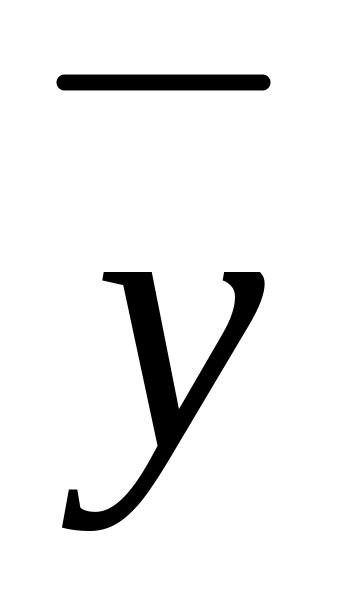 *
пары двойственных задач были
оптимальными, необходимо и достаточно
выполнение условия:
*
пары двойственных задач были
оптимальными, необходимо и достаточно
выполнение условия:х
 (
(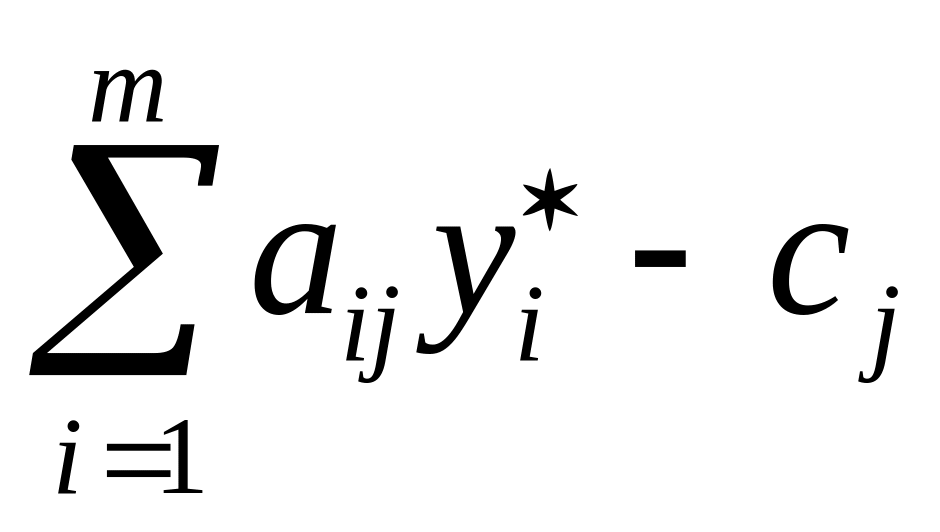 )
= 0, (j
=
)
= 0, (j
=
 )
(5.8.)
)
(5.8.)у
 (
(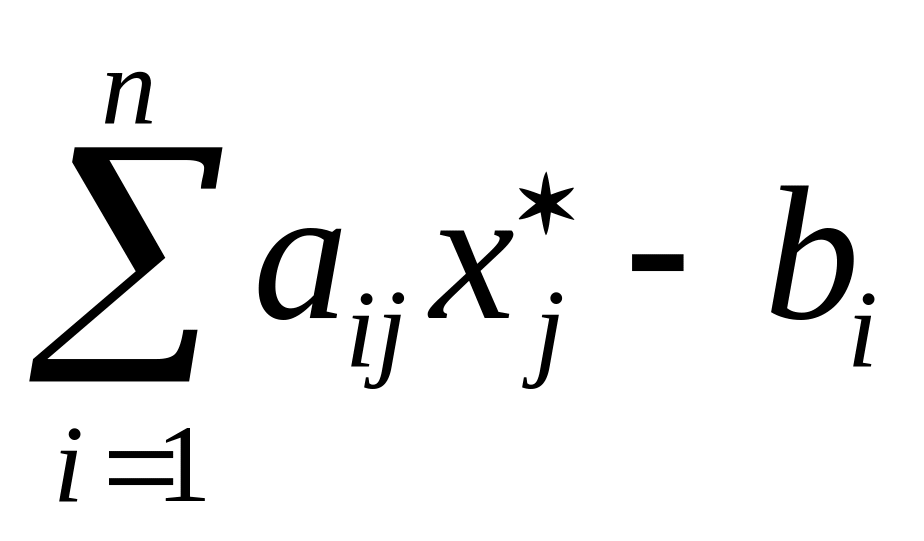 )
= 0, (i
=
)
= 0, (i
=
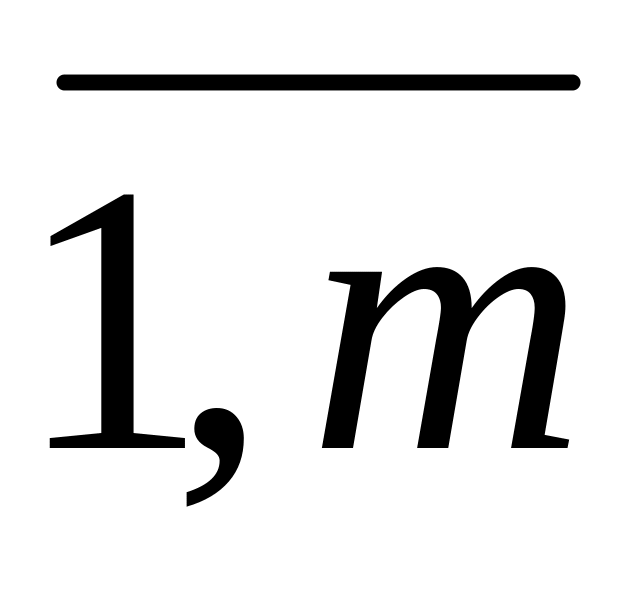 )
(5.9.)
)
(5.9.)
Условия (5.8.) и (5.9.) называются условиями дополняющей нежесткости. Из них следует, что если какое-либо ограничение одной из задач ее оптимальным планом обращается в строгое неравенство, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в строгое равенство.
Что Вы должны знать:
(вопросы для самоконтроля)
Как составить двойственную задачу?
Каковы теоремы двойственности?
Как определить решение двойственной задачи из решения прямой?
Как интерпретировать экономический смысл двойственной задачи?
Пример построения и решения двойственной задачи:
Исходная задача линейного программирования:
F=4X1+6X2 Fmax=?
При ограничениях:
X1+X2<=18
0,5X1+X2<=12
2X1<=27
X2<=9
X1,Х2>=0
Двойственная задача: Найти минимум целевой функции:
Z=18Y1+12Y2+27Y3+9Y4 Zmin=?
Y1+0,5Y2+2Y3>=4
Y1+Y2+Y4>=6
Y1, Y2, Y3, Y4>=0
Исходную задачу можно решить геометрическим способом
Результат :
Х1=12; Х2=6; Fmax=12*4+6*6=84.
Для решения двойственной задачи необходимо найти значения дополнительных переменных Х3, Х4, Х5, Х6 из уравнений:
X1+X2+Х3=18
0,5X1+X2+Х4=12
2X1+ Х5=27
X2+Х6=9
Подставляя значения Х1=12 и Х2=6 в эту систему, найдем значения Х3=0, Х4=0, Х5=3,Х6=3.
По таблице соответствия :
X1 X2 Х3 X4 X5 X6
| | | | | |
Y5 Y6 Y1 Y2 Y3 Y4
Ненулевым значениям Х соответствуют нулевые значения Y, следовательно:
Y3=Y4=Y5=Y6=0
В уравнениях:
Y1+0,5Y2+2Y3-Y5=4
Y1+Y2+Y4-Y6=6
Решая данную систему, получаем Y1=2, Y2=4.
Значение целевой функции
Z=2*18+4*12=84
Таким образом, решена двойственная задача и получено подтверждение первой теоремы.
При решении исходной задачи симплексным методом значения переменных двойственной задачи (Yi) можно найти в F строке с учетом таблицы соответствия.
Примеры для закрепления:
В примерах 1 и 2 построить задачи двойственные к исходным, решить их симплексным методом и найти решения исходных задач, используя решения двойственных.
1) F(x)=2x1+3x2+x3+4x4 min 2) F(x)=x1+2x2+3x3 min
3x1+2x2+x3+6x4>=12 x1-x2+2x3<=1
x1+4x2+2x3+x4>=20 x1 +x3>=1
2x1+x2+8x3+4x4>=8 x2 + x3>=1
x1, x2, x3, x4>=0 x1, x2, x3>=0
