Триангуляция

Далее мы рассмотрим функции геометрического анализа данных. Такой анализ не относится к достаточно распространенным средствам анализа данных, но для специалистов он представляет несомненный интерес.

Пусть есть некоторое число точек. Триангуляция Делоне — это множество линий, соединяющих каждую точку с ее ближайшими соседними точками. Диаграммой Вороного называют многоугольник, вершины которого — центры окружностей, описанных вокруг треугольников Делоне.

Расчет триангуляции

В системе MATLAB определены функции триангуляции Делоне, триангуляции Делоне для ближайшей точки и поиска наилучшей триангуляции. Рассмотрим функции, реализующие триангуляцию Делоне.

• TRI = delaunay(x.y) — возвращает матрицу размера mх3 множества треугольников (триангуляция Делоне), такую что ни одна из точек данных, содержащиеся в векторах х и у, не попадают внутрь окружностей, проходящих через вершины треугольников. Каждая строка матрицы TRI определяет один такой треугольник и состоит из индексов векторов х и у;

• TRI = delaunay('x,у.'sorted'-) — при расчетах предполагается, что точки векторов х и у отсортированы сначала по у, затем по х и двойные точки уже устранены. Пример:

» rand('state',0);

» x=rand(1.25);

» y=rand(1.25); 

» TRI = delaunay(x.y);

» trimeshCTRI,x.y,zeros(size(x)))

» ax1s([0 101]); hold on;

» plot(x.y.'o')

• dsearch(x.y ,TRI ,xi ,yi) — возвращает индекс точки из числа содержащихся в массивах х и у, ближайшей к точке с координатами (xi,y1), используя массив данных триангуляции TRI (триангуляция Делоне для ближайшей точки);

• dsearch(x,y,TRI ,xi ,yi ,S) — делает то же, используя заранее вычисленную разреженную матрицу триангуляции S: S=sparse(TRI(: ,[1 1 2 2 3 3]), TRK: ,[2 3 1 3 1 2]).1.nxy.nxy), где nxy=prod(size(x));

• tsearch(x,y.TRI,xi ,yi) — выполняет поиск наилучшей триангуляции, возвращает индексы строк матрицы триангуляции TRI для каждой точки с координатами (xi ,y1). Возвращает NaN для всех точек, находящихся вне выпуклой оболочки.

Триангуляция трехмерных и n-мерных массивов (п>=2) осуществляется при помощи функций delaunayS и delaunayn соответственно. Эти функции используют не алгоритм вычисления диаграмм Вороного, как del aunay, а алгоритм qhul 1 Национального научно-технического и исследовательского центра визуализации и вычисления геометрических структур США [В MATLAB 6.1 функции delaunay, convhull, griddata, voronoi также используют qhull. - Примеч. ред.].

Построенная по приведенному ранее примеру диаграмма представлена на рис. 6.1.

Рис. 6.1. Пример применения функции delaunay

Нахождение выпуклой оболочки

В системе MATLAB определена функция вычисления точек выпуклой оболочки:

• convhull (х,у) — возвращает индексы тех точек, задаваемых векторами х и у, которые лежат на выпуклой оболочке;

• convhull(x,y,TRI) — использует триангуляцию, полученную в результате применения функции триангуляции Делоне del aunay, вместо того чтобы вычислять ее самостоятельно. Пример:

» хх=-0.8:0.03:0.8;

» уу = abstsqrt(xx));

» [х,у] = po!2cart(xx.yy);

» k = convhuTI(x.y);

» plot(x(k).y(k).'r:',x,y,'g*')

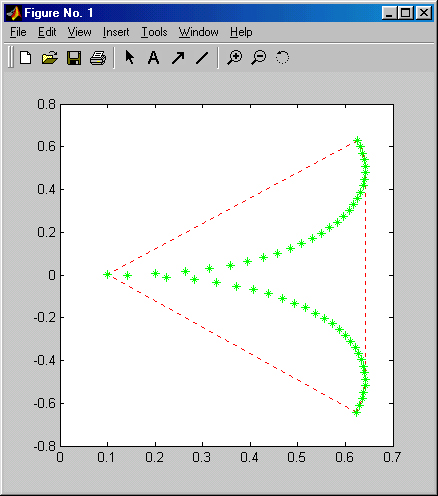
Рис. 6.2. Пример использования функции convhull

Рис. 6.2 иллюстрирует применение функции convhull для построения выпуклой оболочки. Функция convhulln вычисляет n-мерную выпуклую поверхность, основана на алгоритме qhull.

Вычисление площади полигона

В системе MATLAB определены функции, вычисляющие площадь полигона и анализирующие нахождение точек внутри полигона. Для вычисления площади полигона используется функция polyarea:

• polyarea(X.Y) — возвращает площадь полигона, заданного вершинами, находящимися в векторах X и Y. Если X и Y — матрицы одного размера, то polyarea возвращает площадь полигонов, определенных столбцами X и Y;

• polyarea(X.Y.dim) — возвращает площадь полигона, заданного столбцами или строками X и Y в зависимости от значения переменной dim. Пример:

» L = linspace(0.3*pi,10);

» X= sin(L)';

» Y=cos(L)';

» А = polyarea(X.Y)

А =

3.8971 

» plot(X.Y.'m')

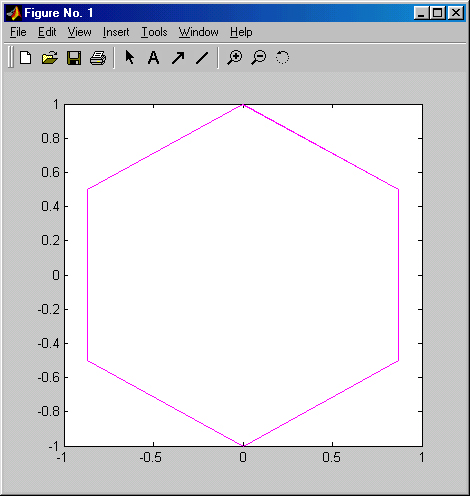
Рис. 6.3. Область многоугольника, для которого вычислена площадь

Построенный по этому примеру многоугольник представлен на рис. 6.3. В данном примере использована функция linspace(xl.x2,N), генерирующая N точек в промежутке от x1 до х2 с последующим формированием векторов X и Y для построения многоугольника в полярной системе координат.

Анализ попадания точек внутрь полигона

Функция Inpolygon используется для анализа того, попадают ли заданные точки внутрь полигона:

• IN=inpolygon(X,Y.xv.yv) — возвращает матрицу IN того же размера, что X и Y. Каждый элемент матрицы IN принимает одно из значений — 1, 0.5 или 0 — в зависимости от того, находится ли точка с координатами (X(p,q),Y(p,q)) внутри полигона, вершины которого определяются векторами xv и yv:

  • IN(p,q) = 1 — если то.чка (X(p.q) ,Y(p,q)) лежит внутри полигона;

  • IN(p,q) = 0.5 — если точка (X(p,q) ,Y(p,q)) лежит на границе полигона;

  • IN(p.q) = 0 — если точка (X(p.q),Y(p,q)) лежит вне полигона. Пример:

» L = linspace(0.2*pi,8);

» yv = sln(L)';

» xv - cos(L)';

» x - randn(l00.l); у = randn(l00.l);

» IN = inpolygon(x.y.xv.yv);

» plot(xv.yv.'k',x(IN),y(IN).'r*'.x(~IN).y(~IN).'bo')

Построенные в этом примере массив точек и полигон представлены на рис. 6.4.

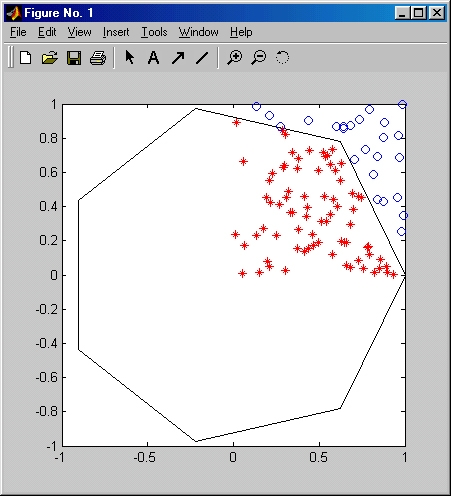
Рис. 6.4. Пример применения функции inpolygon

Точки, попавшие внутрь полигона, обозначены символом звездочки, а точки вне полигона обозначены кружками.

Построение диаграммы Вороного

Для построения диаграммы Вороного служат следующие команды:

• voronoi(x.y) — строит диаграмму Вороного для точек с координатами (х,у). Функция voronoi(х,у,TRI) использует триангуляцию TRI;

• voronoi (...,' LineSpec') — строит диаграмму с заданным цветом и стилем линий;

• [vx.vy] = voronoi (...) — возвращает вершины граней Вороного в векторах vx и vy, так что команда plot(vx,vy,'-' ,х.у,'.') создает диаграмму Вороного.

Пример:

» rand('state'.0):

» x = randd.15): у = randd.15):

» TRI = delaunay(x.y);

» subplotd.2,1)....

» trimesh(TRI,x,y,zeros(s1ze(x))); view(2),...

» axis([0 101]); hold on;

» plot(x.y,'o');

» [vx, vy] = voronoi(x.y.TRI);

» subplot(l,2,2)....

» plot(x,y,'r+',vx,vy,'b-'),...

» axis([0 1 0 1])

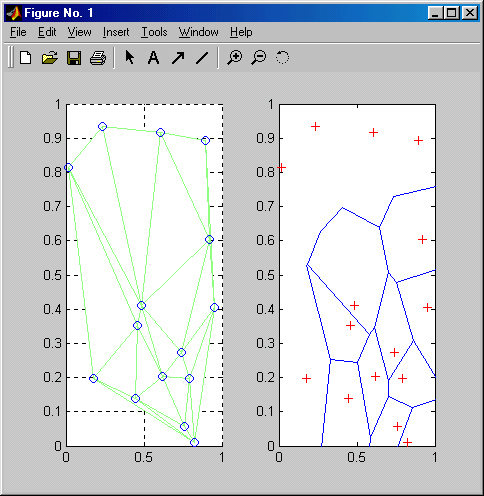
Рис. 6.5. Связь триангуляции Делоне с диаграммой Вороного

Рисунок 6.5 (слева) иллюстрирует построение треугольников Делоне. На рисунке справа изображены знаками «плюс» центры окружностей, проведенных вокруг треугольников Делоне.

Функция [V,C]=voronoin(X) служит для построения диаграмм Вороного n-мерных данных. V — массив граней, С —массив клеток диаграмм. При n=2 вершины граней Вороного возвращаются в порядке смежности, при п>2 — в порядке убывания.