1.3. Кривые Коха

Рассмотрим еще один класс фрактальных структур - так называемые кривые (или фигуры) Коха. На рис. 1.5 показано построение (первые три шага) одной из простейших кривых этого типа. Процедура построения, предложенная фон Кохом, состоит в следующем. Берется отрезок единичной длины и делится на три равные части. Средняя часть заменяется двухзвенной ломаной кривой со звеньями равной длины. В результате возникает ломаная четырехзвенная линия с равными звеньями. На втором шаге с каждым из четырех звеньев проделывается процедура, идентичная описанной. В результате число звеньев ломаной увеличивается в четыре раза и достигнет 16. Затем процесс повторяется с каждым из 16-ти звеньев и так до бесконечности. Таким образом, получается кривая с бесконечно большим числом бесконечно малых звеньев.

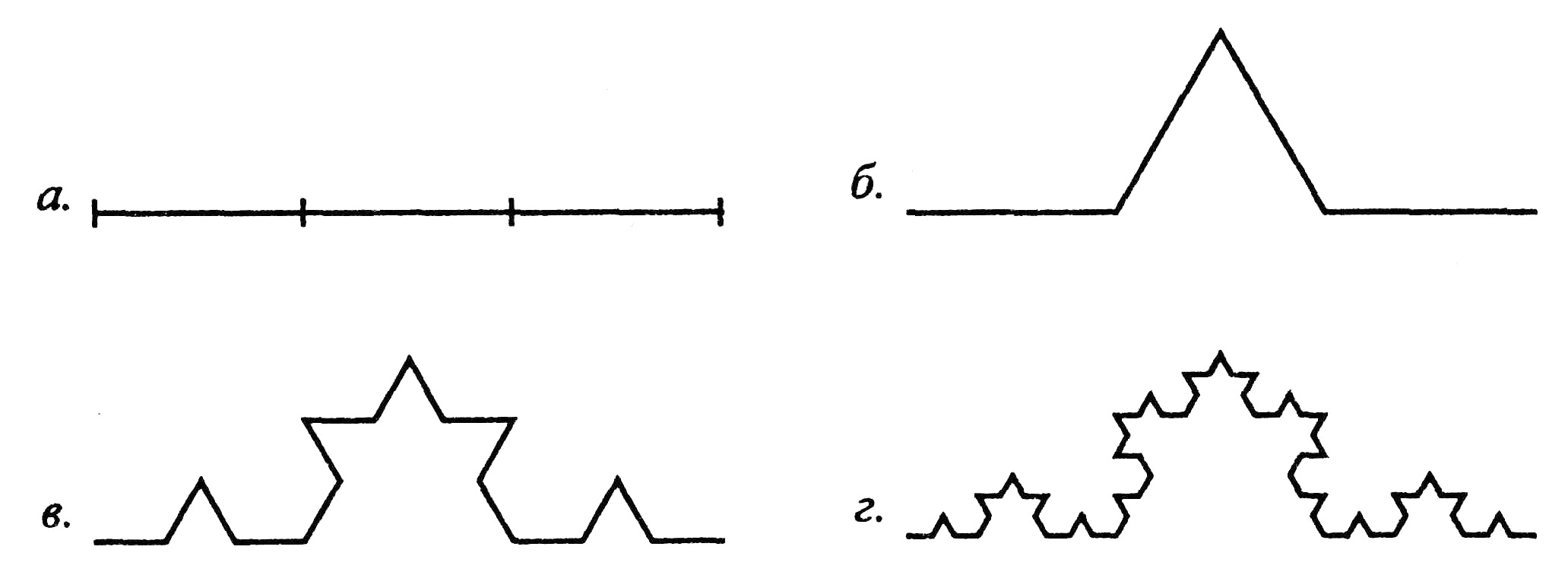
Рис. 1.5. Первые шаги построения одной из кривых Коха

Наконец, алгоритм Коха может быть применен и к замкнутым кривым. Это приводит к образованию так называемых островов Коха – частей плоскости, имеющих конечную площадь, но очень сложную границу. Пример острова Коха, построенного с применением алгоритма рис. 1.5 к сторонам равностороннего треугольника, показан на рис. 1.6.

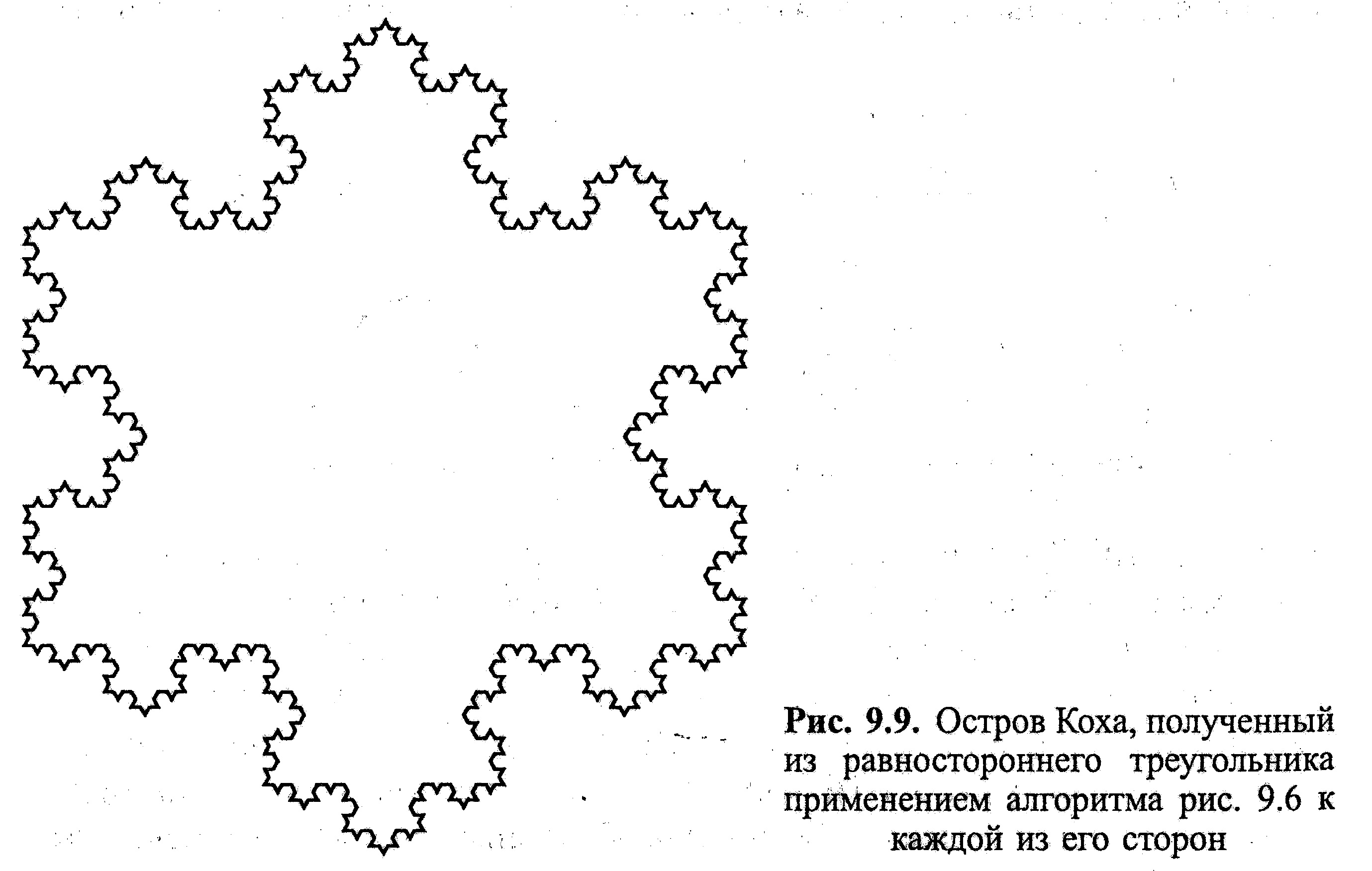
Рис. 1.6. Остров Коха, полученный из равностороннего треугольника применение алгоритма рис. 1.5 к каждой из его сторон

Рис.1.7. Построение квадратной кривой Коха

Кривые Коха имеют различные варианты построения. Рассмотрим, например, квадратичную кривую Коха, построенную с единичным квадратом в качестве затравки и образующим элементом, состоящим из 8-ми ломаных линий (меандра) длиной r = 1/4, изображенных на рис. 1.7.

Частным случаем кривых Коха, изображенным на рис. 1.8. является кривая Мандельброта-Гивена [2]. Образующий элемент для этой кривой делит прямолинейный отрезок на части длиной r = 1/3 и соединяет их в петлю состоящую из трех частей, к которой пристраиваются две ветки. Мандельброт и Гивен использовали эту кривую в качестве моделей перколяционных кластеров. Кривая Мандельброта-Гивена характерна тем, что петли и ветви (выступы) имеют любые размеры. При каждой итерации (переходе от одного поколения предфракталов к следующему образующий элемент производит замену каждого прямолинейного звена в предфрактале на N = 8 звеньев, уменьшенных с r = 1/ 3.

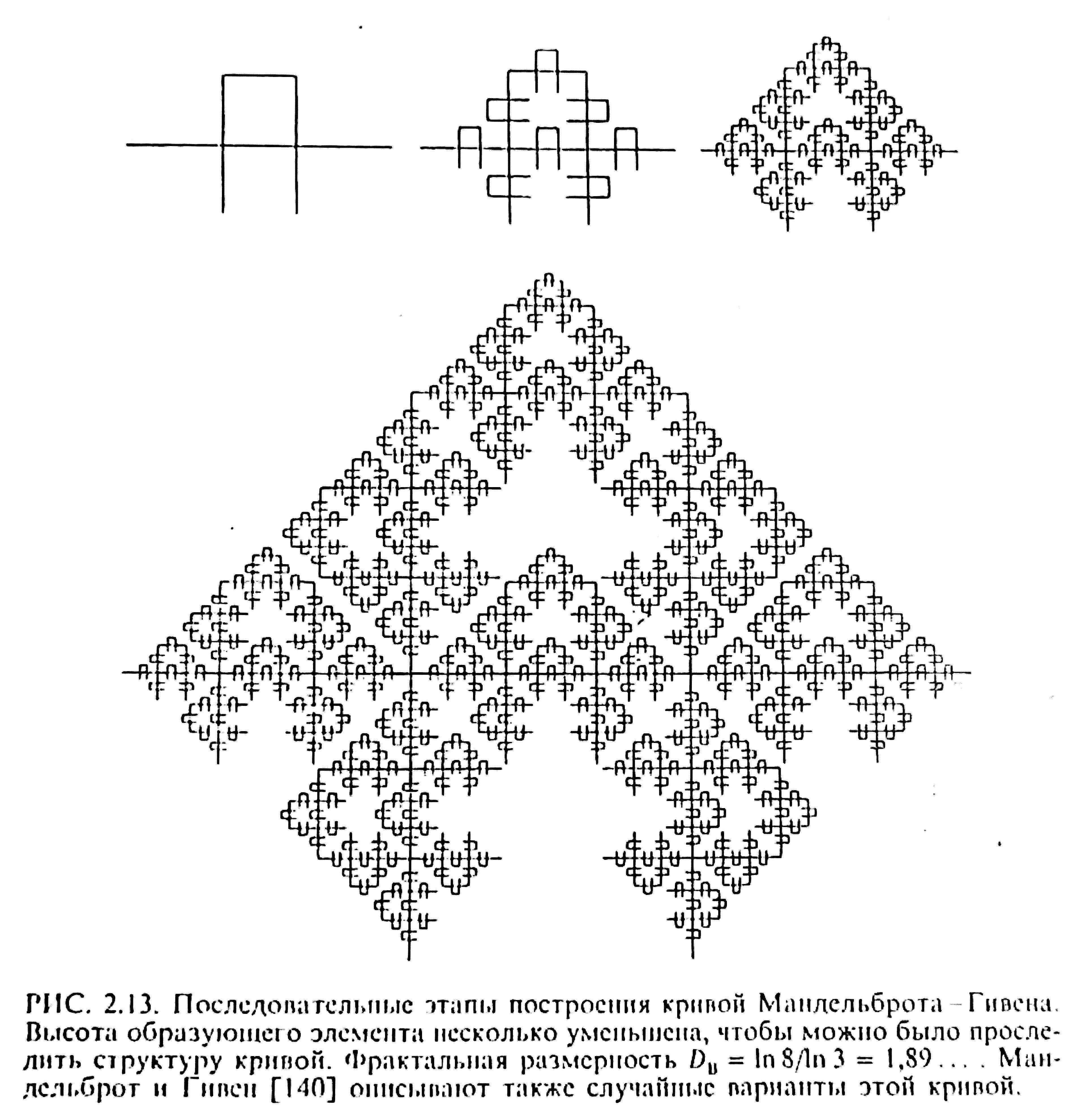
Рис. 1.8. Последовательные этапы построения кривой Мандельброта-Гивена. Высота образующего элемента уменьшена, чтобы можно было проследить структуру кривой.

1.4. Фрактальные множества на плоскости

и в пространстве

Существует построение, породжающее кривую с петлями всех размеров. Это салфетка Серпинского, изображенная на рис. 1.9. В качестве затравки используется часть плоскости, ограниченная треугольником. Образующей элемент исключает из затравки центральный треугольник. Фрактальная структура получается в пределе при бесконечно большом числе итераций.

Рассмотрим построение так называемого ковра Серпинского. Эта процедура показана на рис. 1.10 и состоит в следующем. Берется квадрат со стороной, равной единице. На первом шаге он делится на 9 равных квадратов (со стороной 1/3), и все внутренние точки центрального квадрата удаляются (на рис. 1.10 эта часть заштрихована). На втором шаге так же поступают

Рис. 1.9. Построение салфетки Серпинского

1 2 3 4

Рис. 1.10. Первые шаги построения ковра Серпинского

с оставшимися 8 квадратами, причем возникают уже 64 квадрата (со стороной 1/9). Далее процесс повторяется на всё более и более мелких масштабах. Нетрудно найти, что суммарная площадь выброшенных квадратов равна единице:

, (1.3)

подобно тому, как это имело место в случае канторова множества (см. рис. 1.3). Оставшееся множество точек называется ковром Серпинского. Очевидно, что мощность этого множества равна мощности континуума, поскольку на каждом шаге построения мы проводим процедуру, анало­гичную той, которая выполнялась при построении канторова множества (рис. 1.3 а), с той лишь разницей, что здесь она осуществлена на плоскости (в двух измерениях).

Как видно из приведенного построения, достаточно задать алгоритм одного шага преобразования, чтобы восстановить структуру фрактала на любых масштабах. На рис. 1.11 показаны первые шаги построения некоторых фракталов на плоскости и в 3-мерном пространстве. На этом рисунке шаблон (а) задает рассмотренный выше ковер Серпинского, шаблон (в) есть треугольная кривая Серпинского; шаблон (б) соответствует делению квадрата на 16 частей и удалению четырех внутренних квадратов. Построение трехмерного фрактала (шаблон (д)) состоит в том, что куб делится плоскостями, параллельными его граням, на 27 равных кубов. Центральный куб удаляется. Кроме того, удаляются все кубы, прилегающие к нему по двумерным граням. С каждым из оставшихся 20 кубов проделывается точно такое же построение, в результате чего возникает уже 400 кубов, и т.д. Объект, возникший после бесконечного числа шагов, называется универсальной кривой Менгера. Последняя представляет собой трехмерный аналог канторова множества [3].

Рис. 1.11. Элементарные ячейки шести фракталов

До сих пор мы рассматривали построение фрактала с помощью какого-либо детерминированного алгоритма. В действительности, как это часто имеет место в природе, может использоваться вероятностный алгоритм. При этом свойство самоподобия у таких фракталов сохраняется "в среднем" – после серии реализаций или серии масштабных преобразований.

В качестве примера фрактала в природе рассмотрим явление агрегации [4, 5]. Пусть имеется твердая поверхность, на которую оседают частицы, совершающие случайное блуждание в газе (воздухе). Прилипая к поверхности, частицы меняют ее форму. Очевидно, что вероятность столкнуться с бугорком выше, чем вероятность попасть в яму. В результате этого бугорки начинают расти. По достижении достаточно большого размера бугорки теряют правильную форму – на них появляются ветви и т.д. В результате формируется осадок, имеющий фрактальную структуру (рис. 1.12).

Другим примером вероятностного фрактала являются хорошо известные "морозные" цветы на оконных стеклах.

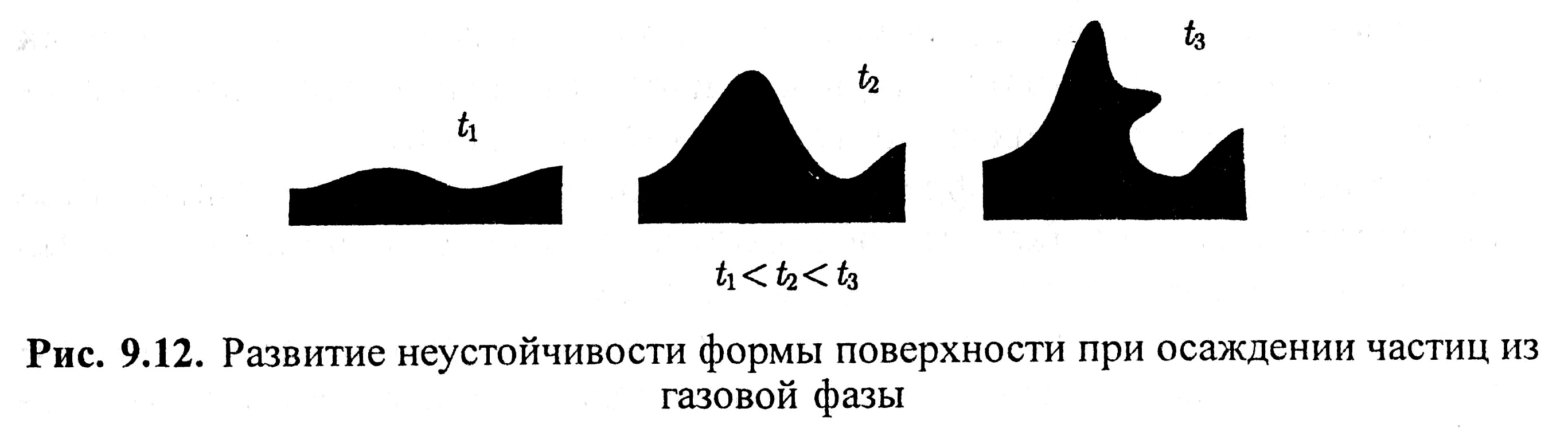
Рис. 1.12. Развитие неустойчивости формы поверхности при осаждении частиц из газовой фазы