1.1. Геометрическое самоподобие

Дж. Пеано построил примеры кривых, целиком заполняющих внутренность квадрата. На рис. 1.1 приведено построение одной из таких кривых (первые 3 шага). На рис. 1.2 показано построение кривой Пеано, равномерно заполняющей треугольник. Самоподобие таких кривых следует из того, что на каждом шаге происходит переход к более мелкому масштабу, но алгоритм преобразования участков кривой остается одинаковым независимо от масштаба (аналогично построению канторовых множеств).

Рис. 1.1. Первые шаги построения кривой Пеано, равномерно заполняющей квадрат

Рис. 1.2. Первые шаги построения кривой Пеано, равномерно заполняющей треугольник

1.2. Канторово множество

Рассмотрим построение классического канторова множества. Возьмем отрезок [0, 1]. Выбросим его среднюю треть, т.е. интервал (1/3, 2/3). Из оставшихся двух отрезков [0, 1/3] и [2/3, 1] выбросим средние трети, т.е. интервалы (1/9, 2/9) и (7/9, 8/9). Из оставшихся четырех отрезков также выбрасываются их средние трети и так до бесконечности. Первые шаги описанного процесса проиллюстрированы на рис. 1.3 а.

а) б)

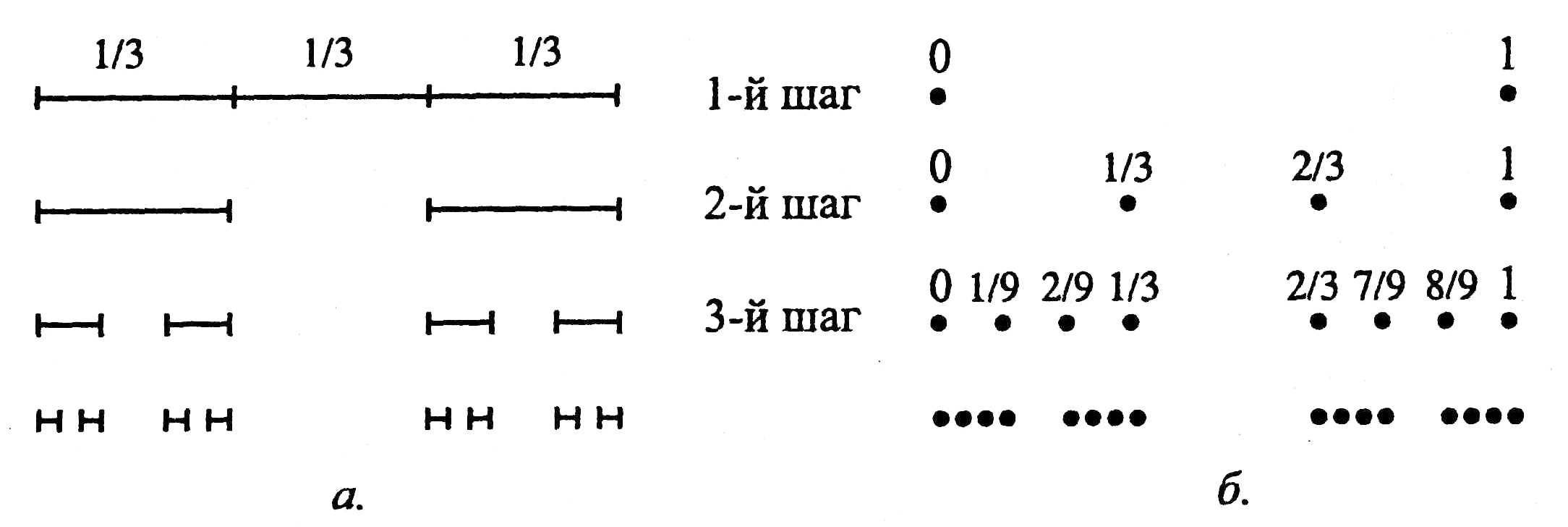
в)

Рис. 1.3. Канторово множество: а – построение путем последовательного удаления интервалов, б – поточечное построение, в – гребень Кантора

После бесконечного процесса "выбраковки" остается некоторое множество точек, которое мы обозначим символом С. Любая точка этого множества может быть представлена в виде

, (1.1)

где числа принимают значения 0 или 2. Множество C называется канторовым). Его мера равна нулю. Действительно, на первом шаге уда­ляется доля отрезка q = 1/3 и остается 1–q. На втором шаге удаляется (1–q)q и остается . На третьем шаге удаляется и остается (1–q)³ и т. д. Итого, удаляемая часть составляет

; . (1.2)

С другой стороны, мощность множества С оставшихся точек равна мощности континуума. Действительно, это множество равномощно множеству всех чисел отрезка [0, 1], что можно показать следующим образом. Представим числа отрезка в двоичной записи: где числа а_п равны 0 или 1. Таким образом, каждому числу А сопоставляется последовательность . Аналогично каждому числу В сопоставляется последовательность { }. Полагая , мы устанавливаем взаимно однозначное соответствие между точками канторова множества и точками отрезка [0, 1]. Следовательно, канторово множество имеет ту же мощность, что и множество точек отрезка, т.е. мощность континуума.

Обратим внимание на одну особенность канторова множества. Возьмем, например, отрезок [0, 1/3] на рис. 1.3 а. Увеличив его в три раза, получим множество , тождественное множеству С, образованному из всего отрезка [0, 1]. Если повторить эту процедуру произвольное число раз (т.е. у множества , возникшего на n-м шаге, выделяется левая треть и эта последняя растягивается в 3 раза, образуя в результате множество C_n+i), то на каждом шаге мы будем приходить к исходному множеству Другими словами, части множества подобны целому множеству. Это свойство самоподобия называют также масштабной инвариантностью или скейлингом.

Построение, аналогичное проведенному выше, можно проделать, осуществляя деление отрезка не на три, а на большее число частей п. При этом число q = 1/3 в приведенном рассуждении следует заменить на q= 1/n. Очевидно, длина выброшенной части отрезка по-прежнему равна 1, а остающееся множество не содержит ни одного целого интервала. Свойство самоподобия сохраняется. Такие множества обладают канторовой структурой. Свойство самоподобия имеет место и для другого множества – канторовой лестницы (часто называемого также "дьявольской лестницей"), имеющего приложения в теории нелинейных динамических систем [3].

На 1-м шаге всем точкам с абсциссами в интервале [1/3, 2/3] присваивается значение 1/2. На втором шаге точкам из интервала [1/9, 2/9] присваивается значение 1/4, а точкам из интервала [7/9, 8/9]

Рис. 1.4. Канторова лестница ("дьявольская лестница")

– значение 3/4 и т. д. В результате возникает функция, первые шаги построения которой показаны на рис. 1.4. Эта функция непрерывна и монотонна, причем ее производная определена и равна нулю на множестве меры 1. Родство канторовой лестницы с канторовым множеством очевидно.