5.2. Кинетические фазовые диаграммы фрактальных и евклидовых форм неравновесного роста льда Ih в переохлажденной воде

Лед (Н₂0) имеет, как известно, одну из наибо­лее сложных фазовых диаграмм: при различных давлениях и температурах наблюдается не менее двенадцати кристаллических и четырех аморф­ных модификаций, в которых молекулы воды со­единены водородными связями в тетраэдральные структуры [106]. Лед обладает полиморфизмом не только на атомном уровне, т.е. в традиционном значении этого понятия, но и "макроскопическим полиморфизмом" - множественностью макроскопических форм кристаллов с определенной атомной структурой, выращенных в сильно неравновесных условиях.

Классическим примером такого макрополи­морфизма является многообразие форм снежи­нок. Большое разнообразие демонстрируют также и фигуры плавления сильно перегретого льда, называемые звездами Тиндаля, которые обнаружены еще в середине XIX века. Важно отметить, что многообразие неравновесных форм роста характерно не только для кристаллов льда, но встречается в природе довольно часто в случае роста кристаллов из расплавов и растворов в сильно неравновесных условиях (высокие переохлаждения или пересыщения), например, при формировании горных пород, образовании минера­лов, быстром затвердевании лавы.

Подобные формы возникают и в результате эволюции неустойчивостей фронтов диффузионного пламени, течения несмешиваемых жидкостей, диффузионной агрегации частиц, химической реакции в пористой среде, роста популяции бактерий и т.д. Большое разнообразие наблюдаемых в природе неравновесных форм роста и отсутствие понимания фундаментальных принципов отбора струк­тур стимулируют исследования, которые в по­следние двадцать лет создали интенсивно разви­вающуюся область нелинейной физики, представляющую интерес для широкого круга специалистов в различных областях естествозна­ния: физической химии, кристаллофизики, гидро­динамики, геологии, минералогии и биологии.

В [142, 143] экспериментально исследовали многообразие неравновесных форм кристаллов гексагонального льда , растущих в сильно переохлажденной бидистиллированной воде. Система лед-вода, с одной стороны, используется здесь в качестве прозрачной модельной системы, позволяю­щей исследовать процессы спонтанного формирования диссипативных структур в сильно нерав­новесных условиях, а, с другой стороны, и сама по себе играет очень важную роль в природе. На ос­нове большого числа (~10³) измерений скорости фазовой границы при различных переохлаждениях в [142, 143] впервые получена полная морфологическая диаграмма системы лед-вода в фазовой плоскости "переохлаждение-скорость роста" в области переохлаждений 0.1 К <  T < 30 К, соответствую­щей гетерогенному механизму зарождения льда в воде при атмосферном давлении ( − температура плавления, Т − температура воды перед началом кристаллизации).

Морфологии неравновесных форм роста кристаллов льда в переохлажденной воде. Эволюцию формы растущих кристаллов льда регистрировали с помощью видеофильмирования в поляризованном свете через микроскоп. Оптические наблюдения показывают, что независимо от уровня исходного переохлаждения начальной формой кристалла льда, свободно растущего от точки касания кристаллом затравки, является плоский диск. Затем контур диска искажается и на нем начинают развиваться выступы. С течением времени эти выступы вырастают в кристаллы различной формы, которая сильно зависит от начального переохлаждения воды.

Рис. 5.6. Неравновесные формы кристаллов льда, растущих из одного центра в области гетерогенного механизма зарождения льда в переохлажденной бидистиллированной воде 0.1 K 30 K: а – фрагмент густой ветвистой структуры, 0.3 K; б – дендрит,

1.5 K; в – иглообразный кристалл, 4.1 K; г – фрактальная игольчатая ветка, 8.2 K; д – фрагмент компактной игольчатой ветки, 14.5 K; е – пластина, 8-30 K.

На рис. 5.6 представлены типичные формы кристалла льда, растущего из первичного выступа при различных переохлаждениях в интервале от 0.1 K до 30 K. Рост льда при 0.4 K характеризуется множественными процессами расщепления вершин «пальцев». В результате, первичный выступ развивается в густую-ветвистую структуру, в которой выделенное направление роста отсутствует (рис. 5.6а). При переохлаждениях выше

0.4 K основной формой кристалла льда является дендрит (рис. 5.6б).

Эти наблюдения хорошо согласуются с известными в литературе результатами исследования кинетики и морфологии роста льда, полученными при относительно небольших переохлаждениях от 0.001 до 1 K [144-149]. Стоит отметить, что морфологический переход от роста, характеризующегося расщеплением вершин «пальцев» к дендритному росту детально исследован в [148]. Было установлено, что естественная конвекция оказывает сильное воздействие на рост кристаллов льда при переохлаждениях менее 0.35 K. В настоящее время отсутствуют систематические исследования кинетики и морфологии роста кристаллов льда при более высоких переохлаждениях, до 30 K.

Наши наблюдения показывают, что с ростом переохлаждения в интервале от 2 до 4 K отношение уменьшается, а значение возрастает ( и - средняя скорость роста боковых ветвей и вершины дендрита соответственно, а – среднее расстояние между вершиной дендрита и позицией, в которой средне-квадратичная амплитуда деформации ствола в виде боковой ветви равна радиусу вершины).

В результате дендрит постепенно «вытягивается» в иглообразный кристалл (рис. 5.6в). Такое поведение растущих дендритов существенно отличается от теоретических представлений. Действительно, согласно диффузионной теории дендритного роста позиция первой боковой ветви, измеренная в единицах радиуса вершины, т.е. / , является параметром, который слабо падает с увеличением переохлаждения [150].

Можно предположить, что наблюдаемый рост кривизны вершины дендрита и величины с ростом исходного переохлаждения воды и, как следствие, постепенная трансформация дендрита в морфологически устойчивую иглу является свидетельством постепенного перехода от диффузионного роста к росту, который контролируется преимущественно механизмом поверхностной кинетики. Поэтому более быстрые неравновесные структуры, растущие при высоких переохлаждениях, должны расти преимущественно в кинетическом режиме кристаллизации.

Видеосъемка процесса роста льда показывает, что при переохлаждениях выше 4.5 K спонтанно формируется древовидная структура, состоящая из нескольких деятков (до сотен) игл (рис. 5.6г). Такую структуру мы называем «игольчатой веткой». В интервале 4.5 16 K могут возникать различные структуры в зависимости от уровня переохлаждения: устойчивая игла, фрактальная игольчатая ветка, компактная игольчатая ветка и пластина (рис. 5.6г, д, е). Особенность этих наблюдений состоит в том, что обнаружены области переохлаждений, в которых могут сосуществовать две или три морфологические фазы. В частности, интервал 4.5 7.5 K соответствует области «естественного отбора» между двумя неравновесными формами: устойчивой иглой и морфологически неустойчивой фрактальной игольчатой веткой.

В интервале от 7.5 K до 12.5 K конкурируют три морфологические фазы: фрактальная и компактная игольчатые ветки, а также пластина. В этом интервале относительное число событий, соответствующих формированию фрактальной ветки с ростом уменьшается, от единицы до нуля, а евклидовых форм (компактной ветки и пластины) относительное число событий возрастает, соответственно, от нуля до единицы. Область переохлаждений 12.5

16 K является областью сосуществования двух форм: компактной игольчатой ветки и пластины. И, наконец, в интервале переохлаждений 16 30 K единственной формой свободно растущего кристалла льда является тонкая пластина.

Рис. 5.7. Зависимость P(A) для игольчатой ветки, растущей при переохлаждении 8.2 K

Рис. 5.8. Фрактальная размерность фрактальных игольчатых веток при различных переохлаждениях

Фрактальную размерность контура проекции игольчатых веток вычисляли по формуле Мандельброта , где P – периметр контура ветки, A – площадь, ограниченная этим кон-туром. На рис. 5.7 показана зависимость P от A в двойных логарифмических координатах для игольчатой ветки, растущей при 8.2 K. Видно, что эта зависимость может быть аппроксимирована прямой линией. Это означает, что контур ветки является фракталом со скейлингом около двух порядков по линейной шкале, а наклон линейной зависимости соответствует фрактальной размерности 1.795±0.004 с коэффициентом корреляции 0.994. Область скейлинга ограничена снизу средним расстоянием между соседними боковыми иглами в структуре фрактальной игольчатой ветки, а сверху – размером всей ветки [160].

Фрактальный анализ изображения ветки в различные моменты времени ее роста показал, что после непродолжительного переходного процесса в начале кристаллизации, связанного с развитием фрактальной ветки из первичного выступа на дисковом кристалле, фрактальная размерность ветки не изменяется со временем, т.е. величина является «хорошим интегралом движения». На рис. 5.8 представлены результаты вычисления

при различных переохлаждениях. Видно, что фрактальная размерность игольчатых веток фактически не зависит от переохлаждения. Оценка фрактальной размерности компактных веток и пластины дает, очевидно, 2 (нефрактальные формы). Таким образом, морфологические переходы между фрактальной веткой и нефрактальными формами (компактной веткой или пластиной) сопровождается скачком фрактальной размерности.

Морфологическая диаграмма υ_t – ΔT. На рис. 5.9 представлены данные измерений средней скорости вершины неравновесной структуры в интервале переохлаждений 0.1 30 K в виде морфологической диаграммы в фазовой плоскости «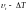 ». Наиболее существенной особенностью этой диаграммы является неоднозначность функции в интервале переохлаждений от

Рис. 5.9. Кинетическая морфологическая диаграмма неравновесных форм роста льда в переохлажденной воде: 1 – густая ветвистая структура, 0.1 0.4 К; 2 – дендрит, 0.4 4 К; 3 – морфологически устойчивая игла, 4.5 7.5 К; 4 – фрактальная игольчатая ветка, 7.5 12.5 К; 5 – компактная игольчатая ветка, 7.5 16; К; 6 – пластина, 8 30 К. В интервале 4.5 7.5 К сосуществуют две морфологические фазы: 3 и 4; в интервале 7.5 12.5 К – три фазы: 4, 5, 6; а в интервале 12.5 16 К – фазы 5 и 6.

4.5 K до 12.5 K. В этой области фазовая диаграмма является бифуркационной с двумя бифуркациями типа «вилки».

Первая вилкообразная бифуркация происходит вблизи точки 4.5 K. Верхняя ветвь функции правее точки представляет данные измерения скорости вершины фрактальной игольчатой ветки, а нижняя ветвь – соответственно данные измерения скорости вершины устойчивой иглы.

Вторая вилкообразная бифуркация происходит вблизи точки 7.5 K. В этом случае верхнюю ветвь зависимости представляет данные нефрактальных форм роста (компактная ветка и пластина), а нижняя ветвь относится к фрактальной игольчатой ветке. Из рис. 5.9 видно, что морфологический переход между устойчивой иглой и пластиной (евклидовы формы) является кинетическим морфологическим переходом первого рода со скачком скорости роста (почти в два раза) вблизи точки перехода, около 7.5 K. В то же время, переход между стабильной иглой и фрактальной веткой и переход между фрактальной и компактной веткой являются бифуркационными морфологическими переходами, так как функция расщепляется в две вилки в точках перехода и соответственно. Переход между компактной веткой и пластиной не сопровождается заметными изменениями скорости роста в пределах точности измерения и зависимости для этих форм роста приблизительно совпадают в интервале морфологической конкуренции 9 K 16 K.

Морфологическая диаграмма . В дискуссии по критериям отбора неравновесных структур, развернувшейся в литературе в последние два десятилетия доминируют две основные гипотезы: гипотеза максимальной средней скорости роста фазовой границы ([151-153] и гипотеза максимальной скорости производства энтропии, применительно к неравновесной кристаллизации, развитой в работах [154-156]).

Так как рост кристалла в сильно переохлажденном расплаве есть рост термодинамически равновесной фазы (твердой) в термодинамически неравновесной фазе (метастабильной жидкости), то принцип максимального производства энтропии эквивалентен принципу максимальной скорости производства твердой фазы, реализующий максимальную скорость приближения к глобальному равновесию системы.

Измерения объема растущих кристаллов с необходимым временным разрешением, особенно разветвленной фрактальной формы, представляет значительные трудности. Использование, например, дилатационных методов, основанных на разнице плотностей фаз, в данном случае осложняется релятивистскими эффектами, которые связаны с тем обстоятельством, что скорости роста кристаллов льда в сильно переохлажденной воде (1-60 см/с) приближаются к скорости поверхностных волн на свободной поверхности воды. Однако из-за сильной анизотропии поверхностной кинетики (скорость роста базисной плоскости на два-три порядка ниже скорости роста призматических плоскостей [157]) кристаллы, растущие в переохлажденной воде, как правило, плоские [146-148]. К тому же, хорошо известно, что рост в плоскостях, перпендикулярных базисной, морфологически устойчив из-за сильной анизотропии поверхностной энергии фазовой поверхности лед-вода, а рост в базисной плоскости морфологически неустойчив из-за слабой анизотропии [148]. Поэтому представляется, что основную информацию об объеме растущего плоского разветвленного кристалла льда несет площадь поверхности проекции, ограниченной контуром кристалла в базисной плоскости.

На рис. 5.10 представлены результаты измерения скорости роста площади растущих структур. Как видно из рисунка, морфологический переход между дендритом и иглой сопровождается изменением знака производной скорости роста площади, т.е. функции

и, поэтому, может быть классифицирован как кинетический морфологический переход второго рода. В тоже время, морфологические переходы между остальными, более холодными структурами, носят явный бифуркационный характер.

В области переохлаждений 4 30 K все морфологические фазы расщеплены по скорости , включая компактную

Рис. 5.10. Зависимость скорости роста площади , ограниченной контуром проекции растущего кристалла, от исходного переохлаждения . Формы роста: 1 – дендрит, 2 – игла, 3 – фрактальная игольчатая ветка, 4 – компактная игольчатая ветка, 5 – пластина.

ветку и пластину, которые в пределах точности эксперимента вырождены по линейной скорости роста (рис. 5.9). Так как по данным видеофильмирования в поляризованном свете толщина кристаллов льда не изменяется скачкообразно при морфологических переходах, а является плавной и медленно меняющейся функцией температуры, то экспериментально полученная в работе фазовая диаграмма качественно отражают характер диаграммы , где V – объем растущего ледяного кристалла.

Как видно, в отличие от морфологической диаграммы « », в построенной диаграмме « » каждая морфологическая фаза представлена отдельной ветвью. С ростом переохлаждения из семейства конкурирующих морфологических фаз отбирается та фаза, которая растет с наибольшей скоростью прироста объема льда. Отсюда следует общий принцип морфологического отбора неравновесных форм роста кристаллов льда: с ростом степени неравновесности системы (переохлаждения воды) отбирается морфологическая фаза, реализующая наибольшую объемную скорость ( ) фазового перехода [165].

Открытым вопросом остается наличие интервалов переохлаждения, в котором одновременно сосуществуют фрактальные и евклидовы морфологические фазы. Этот вопрос требует дальнейших исследований, в частности, изучения влияния внутренних шумов, а также внешних воздействий на ростовое поведение в окрестности точек бифуркации на диаграммах « » и « ».

Следует отметить, что лед имеет двенадцать известных полиморфных модификаций [105]. Кроме того, хорошо известно, что кристаллы льда I_h, растущие из паровой фазы, демонстрируют большое разнообразие неравновесных форм, систематизированных в виде морфологической диаграммы снежинок (диаграмма Накаи [158]). Таким образом, можно говорить о богатом полиморфизме льда на атомном и макроскопическом уровне. Результаты настоящей работы расширяют «макроскопический полиморфизм» льда в отношении к системе лед I_h-вода. Следует также отметить, что теплоемкость переохлажденной воды растет почти по гиперболическому закону в рассматриваемом интервале температур [159]. Переохлажденная вода, таким образом, является нелинейной и неравновесной, т.е. синергетической средой, способной порождать разнообразные диссипативных структур, евклидовых и фрактальных.