11 Аналитическое выравнивание временного ряда с помощью линейной функции
Проведем аналитическое выравнивание для получения математической модели, выражающей общую тенденцию изменения уровней временного ряда.
Рассмотрим выравнивание сглаженного ряда с помощью трёхчленной скользящей средней временного ряда линейной функцией (линейным трендом):
(42)
Параметры
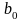и
тренда рассчитаем по МНК.
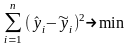(43)
Для поиска параметров уравнения (42) необходимо отсчёт времени производить так, чтобы сумма факторов времени временного ряда удовлетворяла условию:
(44)
Так
как число уровней временного ряда
нечётное, то нулевое значение фактора
времени (t=0)
присутствует. Поэтому периодам времени,
относящимся к середине ряда, присвоим
номера
и
.
Более
ранние от начала отсчёта периоды времени
обозначаются натуральными числами со
знаком минус:
,
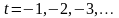а более поздние – натуральными числами
со знаком плюс:
.
Мы
выполнили условие (44).
Теперь найдём параметры уравнения (42) по следующим формулам:
(45)
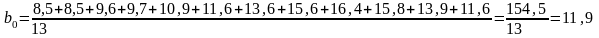
(46)
Теперь приступим к решению уравнения (42):
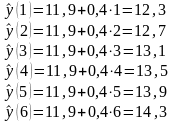
Среднюю ошибку аппроксимациивременного ряда линейным трендом можно определить следующим образом:
(47)
Результаты выравнивания временного ряда с помощью линейной функции
представлены в таблице «см. таблицу 11.1».
Таблица 11.1 – Результаты выравнивания временного ряда с помощью линейной функции
Сглаженные и выровненные уровни ряда |
|
|
|
||||||
Годы |
|
|
|
11,9 |
0,4 |
6,3 |
|||
1998 |
-6 |
8,5 |
9,5 |
|
|
|
|||
1999 |
-5 |
8,5 |
9,9 |
|
|
|
|||
2000 |
-4 |
9,6 |
10,3 |
|
|
|
|||
2001 |
-3 |
9,7 |
10,7 |
|
|
|
|||
2002 |
-2 |
10,9 |
11,1 |
|
|
|
|||
2003 |
-1 |
11,6 |
11,5 |
|
|
|
|||
2004 |
0 |
13,6 |
11,9 |
|
|
|
|||
2005 |
1 |
15,6 |
12,3 |
|
|
|
|||
2006 |
2 |
16,4 |
12,7 |
|
|
|
|||
2007 |
3 |
15,8 |
13,1 |
|
|
|
|||
2008 |
4 |
13,9 |
13,5 |
|
|
|
|||
2009 |
5 |
11,6 |
13,9 |
|
|
|
|||
2010 |
6 |
8,8 |
4,3 |
|
|
|
|||
,ц/га
График линейного тренда представлен в приложении «см. ПРИЛОЖЕНИЕ Г». Линия тренда показывает, что урожайность с каждым годом постепенно растёт.