9 Проверка гипотезы о стационарности временного ряда
Для
ответа на вопрос о стационарности ряда
для урожайности разобьем ряд по времени
на две части: с 1998 по 2004, и 2004 по 2010 гг.
Для стационарного ряда средние уровни
по этим частям не должны существенно
отличаться:
.
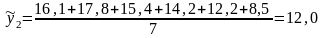
Осуществим статистическую проверку по F-критерию Фишерагипотезы о равенстве дисперсий в сравниваемых частях ряда. Сначала найдём дисперсии в сравниваемых частях временного ряда.
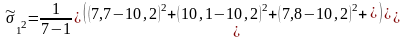
Так
как
>
,
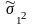то воспользуемся следующей формулой
для F-критерия
Фишера:
(36)
Чтобы
отвергнутьнулевую гипотезу, нужно
доказать существенность расхождения
междудисперсиями
и
при выбранном уровне значимости 
.
Так
как фактическое значение Fф<FТ
,при
числе степеней свободы
,
т.е. 3,6<4,95. В этом случае проверка
равенства средних уровней
и
осуществляется по t-критерию
Стьюдента:
(37)
Так
как
,
то оценка среднеквадратического
отклонения генеральной дисперсии
временного ряда находится по формуле:
(38)
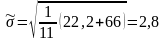
Данные для проверки гипотезы о постоянстве среднего уровня временного ряда представлены в таблице «см. таблицу 9.1».
Таблица 9.1 – Данные для проверки гипотезыо постоянстве среднего уровня временного ряда
|
|
|
|
|
|
|
|
|
|
|
|
7 |
6 |
10,2 |
12,0 |
3,7 |
13,2 |
3,6 |
4,95 |
2,8 |
1,1 |
2,20 |
нет |
?
10 Сглаживание временного ряда методом скользящей средней
Для устранения случайных отклонений экспериментальных значений исходного временного ряда проведем операцию сглаживания временного ряда методом скользящей средней.
Для
этого рассчитаем среднюю величину для
уровня
с помощью трёхчленной средней по
значениям первых трёх уровней
и
:
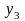(39)
.
Затем
по следующей тройке уровней
и
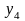находится средняя величина для уровня
и так далее.
Крайние
точки ряда
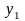и
сглаживают по специальным формулам.
(40)
(41)
Результаты сглаживания временного ряда методом скользящей средней представлены в таблице «см. таблицу 10.1».
Таблица 10.1 – Результаты сглаживания временного ряда методом скользящей средней
Годы |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
yi |
7,7 |
10,1 |
7,8 |
10,9 |
10,3 |
11,5 |
13,0 |
16,1 |
17,8 |
15,4 |
14,2 |
12,2 |
8,5 |
|
8,5 |
8,5 |
9,6 |
9,7 |
10,9 |
11,6 |
13,6 |
15,6 |
16,4 |
15,8 |
13,9 |
11,6 |
8,8 |
Графически сглаженный временной ряд представлен в приложении «см. ПРИЛОЖЕНИЕ Г». Мы видим из графика, что сглаженная функция имеет более мягкие колебания по сравнению с исходным временным рядом. Сглаживание проводится для устранения случайных отклонений экспериментальных значений исходного временного ряда .
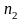
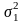
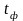