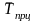7 Линейная диаграмма исходного временного ряда

Урожайность, наблюдаемую в течение определённого периода времени, можно рассматривать как числовые значения статистического показателя в последовательные моменты времени, т.е. в виде временного ряда или ряда динамики.Исходный временной ряд изображен в приложении

«см. ПРИЛОЖЕНИЕ Г».

8 Статистические показатели временно ряда

Вычислим основные показатели временного ряда.

1. Абсолютный прирост (цепной и базисный) определим как разность между двумя уровнями динамического ряда

(22)

При этом индекс заменяем

- для цепного абсолютного прироста: b= i – 1;

- для базисного абсолютного прироста: b = 1.

2. Темп роста(цепной и базисный) рассчитаем по формуле:

(23)

3.Темп прироста(цепной и базисный) найдем из выражения:

(24)

4. Абсолютное значение одного процента прироста(цепного или базисного) равно:

(25)

Результаты вычислений занесены в таблицу «см. таблицу 8.1».

Таблица 8.1 – Аналитические характеристики временного ряда урожайности зерновых

Годы	Урожайность, ц/га	Абсолютный прирост , ц/га		Темп роста Тр , %		Темп прироста Тпр , %		Абсолютное значение 1% прироста α, ц/га
		цепной	базисный	цепной	базисный	цепной	базисный	цепной	базисный
1998	7,7	-	-	-	100,0	-	-	-	0,077
1999	10,1	2,4	2,4	131,2	131,2	31,2	31,2	0,077	0,077
2000	7,8	-2,3	0,1	77,2	101,3	-22,8	1,3	0,101	0,077
2001	10,9	3,1	3,2	139,7	141,6	39,7	41,6	0,78	0,077
2002	10,3	-0,6	2,6	94,5	133,8	-5,5	33,8	0,109	0,077
2003	11,5	1,2	3,8	111,7	149,4	11,7	49,4	0,103	0,077
2004	13,0	1,5	5,3	113,0	168,8	13,0	68,8	0,115	0,077
2005	16,1	3,1	8,4	123,8	209,1	23,8	109,1	0,13	0,077
2006	17,8	1,7	10,1	110,6	231,2	10,6	131,2	0,161	0,077
2007	15,4	-2,4	7,7	86,5	200,0	-13,5	100,0	0,178	0,077
2008	14,2	-1,2	6,5	92,2	184,4	-7,8	84,4	0,154	0,077
2009	12,2	-2,0	4,5	85,9	158,4	-14,1	58,4	0,142	0,077
2010	8,5	-3,7	0,8	69,7	110,4	-30,3	10,4	0,122	0,077

Определим другие показатели ряда динамики.

5. Средний уровень ряда , дисперсию , среднеквадратическое отклонение и коэффициент вариации .

Так как наш ряд интервальный, воспользуемся следующими формулами:

; (26)

; (27)

.

Коэффициент вариации найдем из выражения

(28)

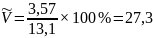
6. Средний (цепнойибазисный) прирост

(29)

7. Средний темп роста, рассчитываемый по формуле средней геометрической:

- Цепной средний темп роста:

(30)

- Базисныйсредний темп роста:

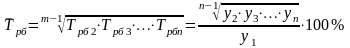(31)

8. Средний темп прироста (цепной и базисный):

(32)

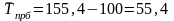
9. Границыварьирования и , которые определяют пределы колебания уровней анализируемого ряда динамики:

y_min=7,7

y_max=17,8

10. Размах вариации

(33)

11. Коэффициент выравненности

(34)

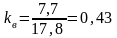
12. Среднее абсолютное отклонение, которое показывает, на сколько ежегодно в среднем изменялась урожайность:

(35)

13. Мода . Моду определим графически по гистограмме выборки «см. ПРИЛОЖЕНИЕ Б».

14. В ранжированном ряду распределения одна половина ряда имеет значения признака больше медианы, а другая – меньше. Так как исследуемый ряд содержит чётное число членов, то номер медианы будет равен:n+1/2=17/2=6

Me=x₆=13,0

В таблице приведены статистические показатели временного ряда «см. таблицу 8.2».

Таблица 8.2 – Статистические показатели временного ряда

										ymin; ymax	R	kв		Mo	Ме
12	10,4	3,2	26,7	0,1	4,6	100,8%	155,4%	0,8%	55,4%	7,7; 17,8	10,1	0,43	3,2	10,5	13,0

Вывод: исходя из данных таблицы, мы видим, что абсолютный базисный прирост всегда положительный, так же как и базисный темп роста. Это говорит о том, что по отношению к первому году урожайность всегда была больше. Но так как цепной прирост был как положительным, так и отрицательным, можно сделать вывод о том, что увеличение урожайности шло неравномерно, были как спады, так и подъёмы.