6 Построение и анализ корреляционной функции ряда распределения
Величина
урожайности
для каждого года
является случайной величиной. Значения
,
рассматриваемые в течение нескольких
лет, образуют последовательность
случайных величин. Между любыми двумя
случайными величинами из этой
последовательности может существовать
связь. Для характеристики такой связи
служит корреляционная функция
Она
является функцией промежутка
между периодами, т.е.
.
Среднее
значение корреляционной функции
для каждого
получим с помощью формулы:
(19)
Этой
формулой рекомендуется пользоваться
при
(где
– интервал наблюдения случайной величины
),
тогда рассчитаем
для
Своё
максимальное значение корреляционная
функция принимает при
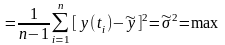(20)
Для
начала вычислим
,
которое равно
.
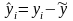Таблица 6.1 – Значения центрированных случайных величин
-
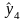
Значение
-4,3
-1,9
-4,2
-1,1
-1,7
-0,5
1,0
4,1
5,8
3,4
2,2
0,2
-3,5
При
При
При
Разделим
на своё максимальное значение
,
получим нормированную корреляционную
функцию (коэффициент корреляции)
:
(21)
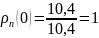
Расчёт эмпирической корреляционной функции представлены в таблице «см. таблицу 6.2».
Таблица 6.2 – Расчёт эмпирической корреляционной функции
|
0 |
|
|
|
|
10,4 |
6,5 |
4,1 |
0,1 |
|
1 |
0,6 |
0,4 |
0,01 |
Проведем выравниваниеэкспериментальныхданныхнормированной эмпирической корреляционной функции с помощью компьютерной программы «Stat 2». Данные, полученные с помощью программы, представлены в таблице «см. таблицу 6.3».График функции, полученной с помощью программы, представлен в «см. ПРИЛОЖЕНИЕ В».
Таблица 6.3 – Расчёт теоретической нормированной корреляционной функции
|
|
|
|
0,282 |
5,798 |
0.0 |
1.000 |
|
|
0.1 |
0.813 |
|
|
0.2 |
0.378 |
|
|
0.3 |
-0.154 |
|
|
0.4 |
-0.608 |
|
|
0.5 |
-0.843 |
|
|
0.6 |
-0.797 |
|
|
0.7 |
-0.499 |
|
|
0.8 |
-0.059 |
|
|
0.9 |
0.376 |
|
|
1.0 |
0.667 |
|
|
|
|
|
|
1.1 |
0.730 |
|
|
1.2 |
0.557 |
|
|
1.3 |
0.216 |
|
|
1.4 |
-0.175 |
|
|
1.5 |
-0.489 |
|
|
1.6 |
-0.630 |
|
|
1.7 |
-0.562 |
|
|
1.8 |
-0.319 |
|
|
1.9 |
0.012 |
|
|
2.0 |
0.321 |
|
|
2.1 |
0.511 |
|
|
2.2 |
0.528 |
|
|
2.3 |
0.376 |
|
|
2.4 |
0.112 |
|
|
2.5 |
-0.173 |
|
|
2.6 |
-0.387 |
|
|
2.7 |
-0.466 |
|
|
2.8 |
-0.393 |
|
|
2.9 |
-0.198 |
|
|
3.0 |
0.049 |
|
|
3.1 |
0.267 |
|
|
3.2 |
0.388 |
|
|
3.3 |
0.379 |
|
|
3.4 |
0.249 |
|
|
3.5 |
0.047 |
|
|
3.6 |
-0.158 |
|
|
3.7 |
-0.302 |
|
|
3.8 |
-0.342 |
|
|
3.9 |
-0.271 |
|
|
4.0 |
-0.117 |
|
|
4.1 |
0.066 |
|
|
4.2 |
0.217 |
|
|
4.3 |
0.291 |
|
|
4.4 |
0.269 |
|
|
4.5 |
0.162 |
|
|
4.6 |
0.009 |
|
|
4.7 |
-0.138 |
|
|
4.8 |
-0.233 |
|
|
4.9 |
-0.249 |
|
|
5.0 |
-0.184 |
|
|
5.1 |
-0.065 |
|
|
5.2 |
0.069 |
|
|
5.3 |
0.174 |
|
|
5.4 |
0.217 |
|
|
|
|
|
|
5.5 |
0.189 |
|
|
5.6 |
0.102 |
|
|
5.7 |
-0.012 |
|
|
5.8 |
-0.117 |
|
|
5.9 |
-0.178 |
|
|
6.0 |
-0.179 |
|
|
6.1 |
-0.123 |
|
|
6.2 |
-0.031 |
|
|
6.3 |
0.066 |
|
|
6.4 |
0.137 |
|
|
6.5 |
0.160 |
|
|
6.6 |
0.131 |
|
|
6.7 |
0.062 |
|
|
6.8 |
-0.023 |
|
|
6.9 |
-0.096 |
|
|
7.0 |
-0.134 |
|
|
7.1 |
-0.128 |
|
|
7.2 |
-0.081 |
|
|
7.3 |
-0.011 |
|
|
7.4 |
0.059 |
|
|
7.5 |
0.106 |
|
|
7.6 |
0.117 |
|
|
7.7 |
0.090 |
|
|
7.8 |
0.036 |
|
|
7.9 |
-0.027 |
|
|
8.0 |
-0.077 |
|
|
8.1 |
-0.101 |
|
|
8.2 |
-0.090 |
|
|
8.3 |
-0.052 |
|
|
8.4 |
0.001 |
|
|
8.5 |
0.050 |
|
|
8.6 |
0.081 |
|
|
8.7 |
0.085 |
|
|
8.8 |
0.061 |
|
|
8.9 |
0.019 |
|
|
9.0 |
-0.027 |
|
|
9.1 |
-0.061 |
|
|
9.2 |
-0.075 |
|
|
9.3 |
-0.063 |
|
|
9.4 |
-0.032 |
|
|
9.5 |
0.007 |
|
|
|
|
|
|
9.6 |
0.042 |
|
|
9.7 |
0.062 |
|
|
9.8 |
0.061 |
|
|
9.9 |
0.040 |
|
|
10.0 |
0.008 |
