3 Построение диаграммы накопленных частот и гистограммы выборки

Диаграмма накопленных частот строится по формуле:

, (7)

где у – число элементов в выборке, для которых значение ;

n – объём выборки.

Она является эмпирическим аналогом интегрального закона функции распределения. Результаты расчёта представлены в таблице «см. таблицу 3.1».

Таблица 3.1 – Данные для построения диаграммы накопленных частот

x<x1

x<x2

x<x3

x<42

x<x5

x<x6

x<x7

x<x8

x<x9

x<x10

x<x11

x<x12

x<x13

x<∞

0

1/13

2/13

3/13

4/13

5/13

6/13

7/13

8/13

9/13

10/13

11/13

12/13

1

1. Определяем число интервалов k, на которую мы должны разбить ось 0х, по формуле Стерджесса:

(8)

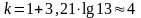
2. Определяем длину интервала по следующей формуле:

(9)

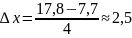
3. Примем за центр некоторого интервала середину области изменения изучаемого признака:

(10)

Сделаем корректировку числа интервалов, k=5.

4. Рассчитываем частоту ряда распределения .

5.Подсчитаем относительное количество элементов (частость) совокупности, попавших в данный интервал.

6. Построим гистограмму «см. ПРИЛОЖЕНИЕ Б», представляющую собой ступенчатую кривую, значение которой на -м интервале постоянно и равно ( ) .

Результаты расчёта представлены в таблице «см. таблицу 3.2».

Таблица 3.2–Данные для построения гистограммы выборки

			3	4	5
	(6,7;9,2]	(9,2;11,7]	(11,7;14,2]	(14,2;16,7]	(16,7;19,2]
	3	4	3	2 xmin = x1	1
	0,10	0,12	0,10	0,06	0,03

4Проверка основной гипотезы распределения

Для проверки гипотезы о нормальном законе изучаемого распределения воспользуемся следующим критерием.

Если выборочные асимметрия и эксцесс удовлетворяют неравенствам, то изучаемое распределение можно считать нормальным.

_; (11)

_. (12)

Рассчитаем выборочные асимметрию и эксцесс:

(13)

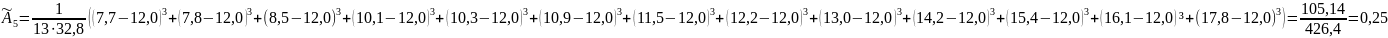
(14)

Дисперсия асимметрии и дисперсия эксцесса , входящие в выражения (17) и (18), вычисляются по формулам:

; (15)

. (16)

Данные для проверки основной гипотезы представлены в таблице « см. таблицу 4.1».

Таблица 4.1– Данные для проверки основной гипотезы

				Выполнение критерия
0,25	1,7	1,2	3,9	Да