14 Количественная оценка риска

Под риском обычно понимают возможность наступления одного или нескольких случайных событий, являющихся причиной отклонения полученного результата от ожидаемого значения.

Оценим риск неурожайности 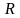, с помощью коэффициента вариации . Чем больше величина показателя вариации, тем выше рассеяние и больше риск.

(58)

Рассчитаем значение коэффициента вариации урожайности для последних пяти лет, используя сведения об урожайности предыдущих пяти лет.

Для этого нам необходимо рассчитать выборочное среднее и среднеквадратическое отклонение урожайности за предыдущие 5 лет для каждого года.

Теперь мы можем найти риски неурожайности:

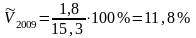
Расчёт уровня риска не урожайности представлен в таблице «см. таблицу 14.1».

Таблица 14.1 – Расчёт уровня риска неурожайности

Годы	2006	2007	2008	2009	2010
Уровень риска , %	18,5	22,6	16,9	11,8	13,9

Линейная диаграмма изменения уровня риска представлена в приложении «см. ПРИЛОЖЕНИЕ Е».

Вывод: исходя из таблицы 14.1 видно, что риск неурожайности изначально возрастал, к 2007 году он стал меньше.

Заключение

1. Вариант курсовой работы 6 (Верхнеуральский район).

2. Был составлен ранжированный вариационный ряд распределения, который показывает конкретные значения варьирующего признака (урожайности картофеля).

3. Проведена оценка среднего значения, дисперсии, среднеквадратического отклонения, коэффициента вариации. Определен доверительный интервал для генеральной средней, т.е. выход за пределы доверительного интервала имеет малую вероятность (q=0,05).

4. Была построена диаграмма накопленных частот, в каждой точке х имеет скачек, равный 1/n (см. Приложение А). Построена гистограмма выборки, которая включает в себя 5 интервалов (К=5), длина интервала Δх = 2,5; центром является точка 10,5, каждый интервал включает в себя от 2 до 6 элементов совокупности

5. Проверена гипотеза о нормальном законе распределения при n=13 с помощью показателей выборочной асимметрии и эксцесса. Изучаемое распределение можно считать нормальным.

6. Проведено выравнивание функции распределения с помощью программы «Stat1», т.е. мы подобрали кривую распределения, которая наилучшим образом описывает эмпирические данные распределения. Были определены новые значения среднего значения, дисперсии, среднеквадратического отклонения.

7. Произведено построение и анализ корреляционной функции ряда распределения. Корреляционная функция характеризует связь между двумя случайными величинами. Произведен расчет корреляционной функции при ; 1; 2;3, и, соответственно значения этой функции . С помощью программы «Stat 2» проведено выравнивание данных корреляционной функции и затем построена кривая корреляционной функции, которая носит колебательный характер, колебания с течением времени затухают. Наблюдается элемент периодичности.

8. Построена линейная диаграмма исходного временного ряда на основе исходных данных об урожайности (см. Приложение Г). Наблюдаемую урожайность мы можем рассматривать в виде временного ряда или ряда динамики.

9. Вычислены основные показатели временного ряда: абсолютный прирост (цепной и базисный), темп роста (цепной и базисный), темп прироста (цепной и базисный), абсолютное значение прироста (цепной и базисный). А также другие показатели динамики: средний уровень ряда, дисперсия, средний прирост (цепной и базисный), средний темп роста (цепной и базисный), средний темп прироста (цепной и базисный), границы варьирования (определяют пределы колебания уровней данного ряда динамики), размах вариации, коэффициент выравненности, среднее абсолютное отклонение, моду и медиану.

10. Проверена гипотеза о стационарности временного ряда. Для этого ряд урожайности был разделен на 2 равные части и определены дисперсии для каждой из них. Найдено фактическое (расчетное) значение F-критерия Фишера, которое в данном случае меньше F-табличного. Следовательно, гипотеза о равенстве дисперсий подтверждается. Найдено значение t-критерия Стьюдента, которое меньше t-табличного. Выровненная нормированная корреляционная функция имеет явную тенденцию стремиться к нулю с течением времени (затухающие колебания). Следовательно, предположение об эргодичности и стационарности временного ряда является верным

11. Проведено сглаживание временного ряда методом скользящей средней для того чтобы устранить случайные отклонения значений исходного временного ряда. Для этого мы рассчитываем среднюю (сглаженную) величину для каждого значения .

12. Проведено аналитическое выравнивание временного ряда с помощью линейной функции. Это необходимо для получения математической модели, выражающей общую тенденцию изменения уровней временного ряда. На графике линейного тренда мы видим, что линия линейного тренда имеет минимальное отклонение от своего среднего значения, в отличие от исходного временного ряда и сглаженного временного ряда

13. Проведено экспоненциальное сглаживание временного ряда для того чтобы придать значение более поздним наблюдениям, чем ранним. Найдены значения экспоненциальных средних 1го и 2го порядка. Построив линейную диаграмму, включающую в себя исходный временной ряд, временной ряд, сглаженный методом скользящей средней, временной ряд, сглаженный методом экспоненциальной средней 1-го порядка и 2-го порядка, мы видим, что экспоненциальная средняя 1го порядка практически пошагово копирует исходный временной ряд, но с запозданием на 1 год.

14. Построено прогнозирование временного ряда на основе экспоненциального сглаживания. Сделан прогноз на 2010 год. Мы сравнили его с фактическим: = 20,5; = 13,5; ошибка прогноза Δ =7.

15. Проведена количественная оценка риска неурожайности.