4.4.Нахождение решения двойственной задачи по известному решению

прямой задачи

Предположим, что симплексным методом найдено оптимальное решение Х^* прямой задачи и оно определяется базисом А₁,А₂,...,А_т . Обозначим С_б^*= (с₁,с₂,...,с_т) – вектор-строку, составленную из коэффициентов при переменных целевой функции. Пусть D – матрица, составленная из координат векторов-условий первой симплексной таблицы, ее столбцы расположены над базисными столбцами последней таблицы оптимального решения. D^-1 – матрица, обратная к матрице D. Ее вычислять не следует. Она находится в последней симплексной таблице. Ее столбцы расположены под столбцами, единичных базисных векторов первой таблицы.

Теорема 2. Если прямая задача линейного программирования имеет оптимальное решение Х^*, то Y^* = С_б^* D^-1 является оптимальным решением двойственной задачи.

Пример 2. Найти решение данной и двойственной к ней:

Z(X) = x₁ – 6x₂ + 2x₃ –x₄ + 3x₅  max,

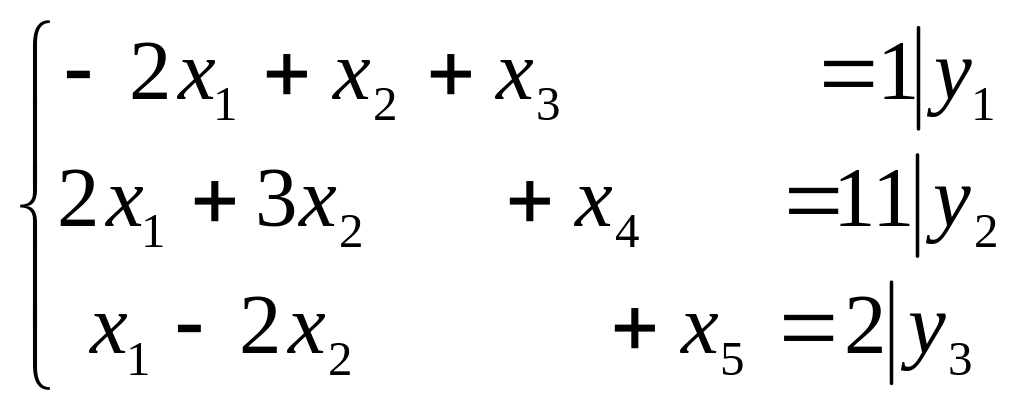
□ Двойственная задача имеет вид:

F(Y) = y₁ + 11y₂ + 2y₃  min,

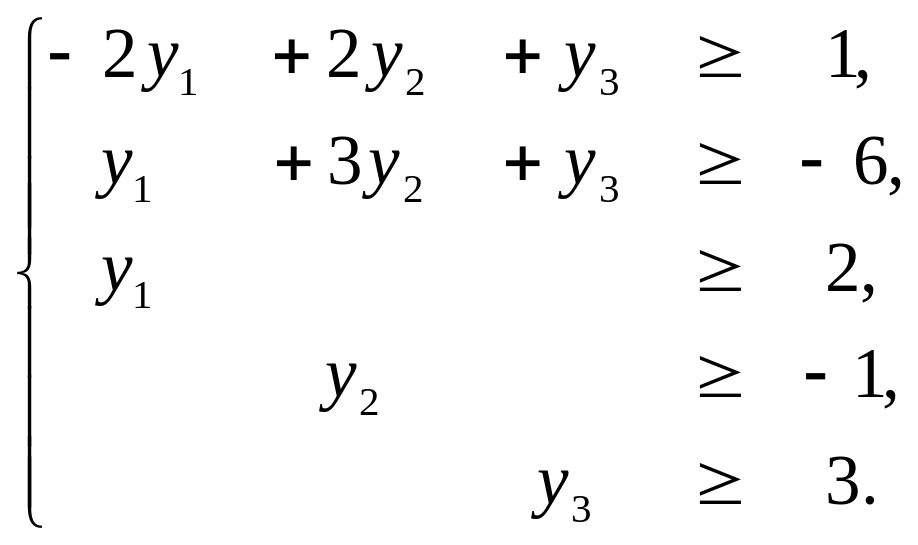
В данной паре задач легче решить исходную задачу, так как она имеет начальное опорное решение Х₁ = (0,0,1,11,2) с базисом Б₁ = (А₃,А₄,А₅) и ее без дополнительных преобразований можно решить симплексным методом. Решение исходной задачи приведено в таблице:

1 -6 2 -1 3

Б	Сб	А0	А1	А2	А3	А4	А5
А3 А4 А5	2 -1 3	1 11 2	-2 2 [1]	1 3 -2	1 0 0	0 1 0	0 0 1
	к	Z1=-3	-4	-1	0	0	0
А3 А4 А1	2 -1 1	5 7 2	0 0 1	-3 [7] -2	1 0 0	0 1 0	2 -2 1
	к	Z2=5	0	-9	0	0	4
А3 А2 А1	2 -6 1	8 1 4	0 0 1	0 1 0	1 0 0	3/7 1/7 2/7	8/7 -2/7 3/7
	к	Z3=14	0	0	0	9/7	10/7

Оптимальным решением исходной задачи является вектор Х^* =(4,1,8), базис оптимального решения Б^* = (А₃,А₂,А₁), значение целевой функции max Z(X) = 14.

Оптимальное решение двойственной задачи находим по формуле

Y^* = C^*D^-1 =

Здесь матрица D^-1 находится в последней таблице под базисными столбцами А₃,А₄,А₅ первой таблицы.

Данное решение можно найти также по формулам:

y_i = i^* + c_i^*.

у₁ = 0 + 2 =2, у₂ =9/7-1= 2/7, y₃ = 10/7 + 3 = 31/7.

Таким образом, оптимальным решением двойственной задачи задачи является вектор У^*= (2, 2/7, 31/7), minF(Y^*) = 14 .

Ответ: max Z(X) = 14 , X^* = (4,1,8), min F(Y)= 14, Y^* = (2, 2/7, 31/7)