2.1 Приклад виконання завдання

По похилій площині (рис. 2.6) призми 1 масою m₁=10кг спускається вантаж 2 (m₂=6кг), який тягне за допомогою невагомої нитки вантаж 3 масою m₃=4кг.

Знайти переміщення призми 1 по гладенькій горизонтальній площині, якщо тіло m₂ опустилось по похилій площині на S=0,5м.

Розв’язання. Покажемо зовнішні сили, які прикладені до матеріальної системи, що складається з призми 1 та тіл 2, 3. Такими силами є: P₁=m₁g – сила ваги призми, P₂=m₂g i P₃=m₃g – вага відповідно другого та третього вантажів, N – реакція гладенької горизонтальної поверхні.

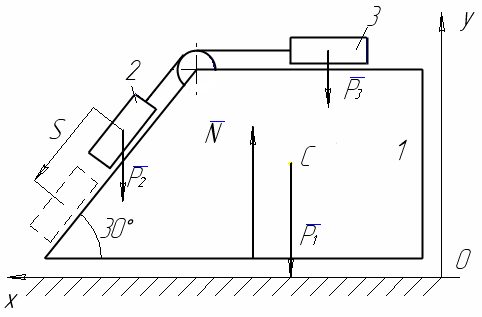
Рисунок 2.6

Запишемо теорему про рух центра мас матеріальної системи в проекціях на вісь Х:

, (2.1)

де , - проекція головного вектора зовнішніх сил на вісь Х.

Оскільки = 0, то = 0. Тоді .

В початковий момент часу система знаходилась у спокої і тому . Із формули (2.1) маємо:

.

Таким чином, координата Х_С центра мас матеріальної системи залишається сталою незалежно від переміщень тіл, що входять у систему.

Визначимо положення центра мас системи в початковий момент часу:

. (2.2)

Якщо вантаж 2 переміститься на величину , тоді тіло 3 – на , а призма 1 - і положення Х_С центра мас знайдемо за формулою:

. (2.3)

Враховуючи (2.2), із формули (2.3) отримаємо:

. (2.4)

Переміщення та складається із відносного по призмі і переносного разом із призмою.

Тепер із формули (2.4) знаходимо переміщення призми.

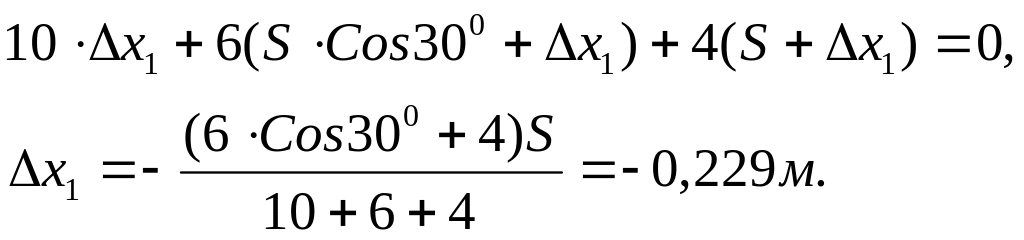
Знак “мінус” вказує на те, що призма 1 перемістилася в сторону, протилежну додатному напрямку осі Х.

Відповідь: призма 1 перемістилась вправо на 0,229 м.

Д. 3 Використання теореми про зміну головного вектора кількості руху системи для дослідження переміщення тіл

Електродвигун 1 (рис. 3.1 – 3.10 ) масою m₁ приєднується до системи нездеформованих пружин. На тілі 2 масою m₂ (однорідний диск радіуса R – варіант 1, 4, 7, 10, 13, 16, 19, 22, 25, 28; кільце радіуса R – варіант 2,5,8,11,14,17,20,23,26,29; однорідний стержень ОА = R – варіант 3,6,9,12,15,18,21,24,27,30 ), що з’єднане з ротором електродвигуна 1, закріплена матеріальна точка масою m_А на відстані ОА від осі ротора електродвигуна. Ротор обертається з постійною кутовою швидкістю ω. Пружини приєднані до електродвигуна таким чином, що його статор переміщується поступально, а точка 0 по осі х

Знайти закон руху корпуса електродвигуна, центр мас якого О переміщується по вертикалі, побудувати графік руху точки О протягом одного періоду при кутовій швидкості ω = n∙ ρ (ρ – частота, при якій спостерігається явище резонансу), якщо в початковий момент часу точка О зміщена із положення рівноваги на величину λ₀ і їй була надана швидкість ν₀, а тіло 2 почало обертатись навколо горизонтальної осі О з кутовою швидкістю ω.

Необхідні для розрахунку дані наведені в табл. 3.1.

Таблиця 3.1

Варіант	m1, кг	m2, кг	mА, кг	R, м	с1, Н/м	с2, Н/м	с3, Н/м	n	λ0, м	ν0, м/с
1	15	2	0,6	0,2	2·103	3·103	1,5·103	0,7	3·10-2	0
2	18	3	0,7	0,21	3·103	2·103	4·103	0,65	2,5·10-2	1,5
3	21	4	0,8	0,22	4·103	1·103	5·103	1,2	2·10-2	0,5
4	23	5	0,9	0,25	5·103	6·103	1·103	0,63	-1,5·10-2	2
5	25	6	1,0	0,3	6·103	4·103	2·103	0,75	-10-2	-1,5
6	10	1	0,5	0,15	1·103	8·103	3·103	0,8	0	3
7	12	1,5	0,6	0,16	2·103	3·103	5·103	0,55	5·10-2	4
8	13	2,5	0,7	0,17	3·103	7·103	2·103	1,3	4·10-2	-2,5
9	17	3,5	0,8	0,18	4·103	9·103	1·103	1,25	-3,5·10-2	0,5
0	19	4,5	0,9	0,19	5·103	3·103	6·103	1,3	0,5·10-2	-2,5

Рисунок 3.1

Рисунок 3.2

Рисунок 3.3

Рисунок 3.4

Рисунок 3.5

Рисунок 3.6

Рисунок 3.7

Рисунок 3.8

Рисунок 3.9

Рисунок 3.10