Динаміка системи

Д.2 Використання теореми про рух центра мас для визначення переміщення тіл

Визначити переміщення призми 1 (рис. 2.1-2.5) по горизонтальній гладенькій поверхні, якщо центр мас тіла 2 опустився на відстань S відносно призми 1 (схеми 1-19) або тіло 2 повернулося на заданий кут навколо горизонтальної осі (схеми 20-30). В початковий момент часу матеріальна система знаходиться у спокої.

Дані для розрахунків наведені в табл. 2.1 ( ).

Таблиця 2.1

В-т	Рисунок 1-19							Рисунок 20-30
	S, м	m ,кг	m ,кг	m3,кг	град	R,м	r,м	m кг	m кг	m3 кг	град	l, м
1 2 3 4 5 6 7 8 9 0	0,3 0,2 0,4 0,1 0,5 0,6 0,7 0,15 0,35 0,25	2 3 4 5 6 7 8 9 8 7	4 2 1 3 5 2 3 4 5 3	3 1 2 4 3 4 2 3 4 2	30 45 60 30 45 60 30 45 60 30	0,4 0,3 0,2 0,1 0,15 0,25 0,35 0,45 0,5 0,3	0,3 0,2 0,15 0,05 0,1 0,2 0,3 0,4 0,25 0,15	1 2 3 4 5 6 7 6 5 4	2 1 4 3 2 4 3 2 4 3	3 1.5 2 1 3 5 4 5 3 2	60 45 30 60 45 30 60 45 30 60	0,3 0,4 0,5 0,2 0,1 0,15 0,25 0,35 0,45 0,55

Р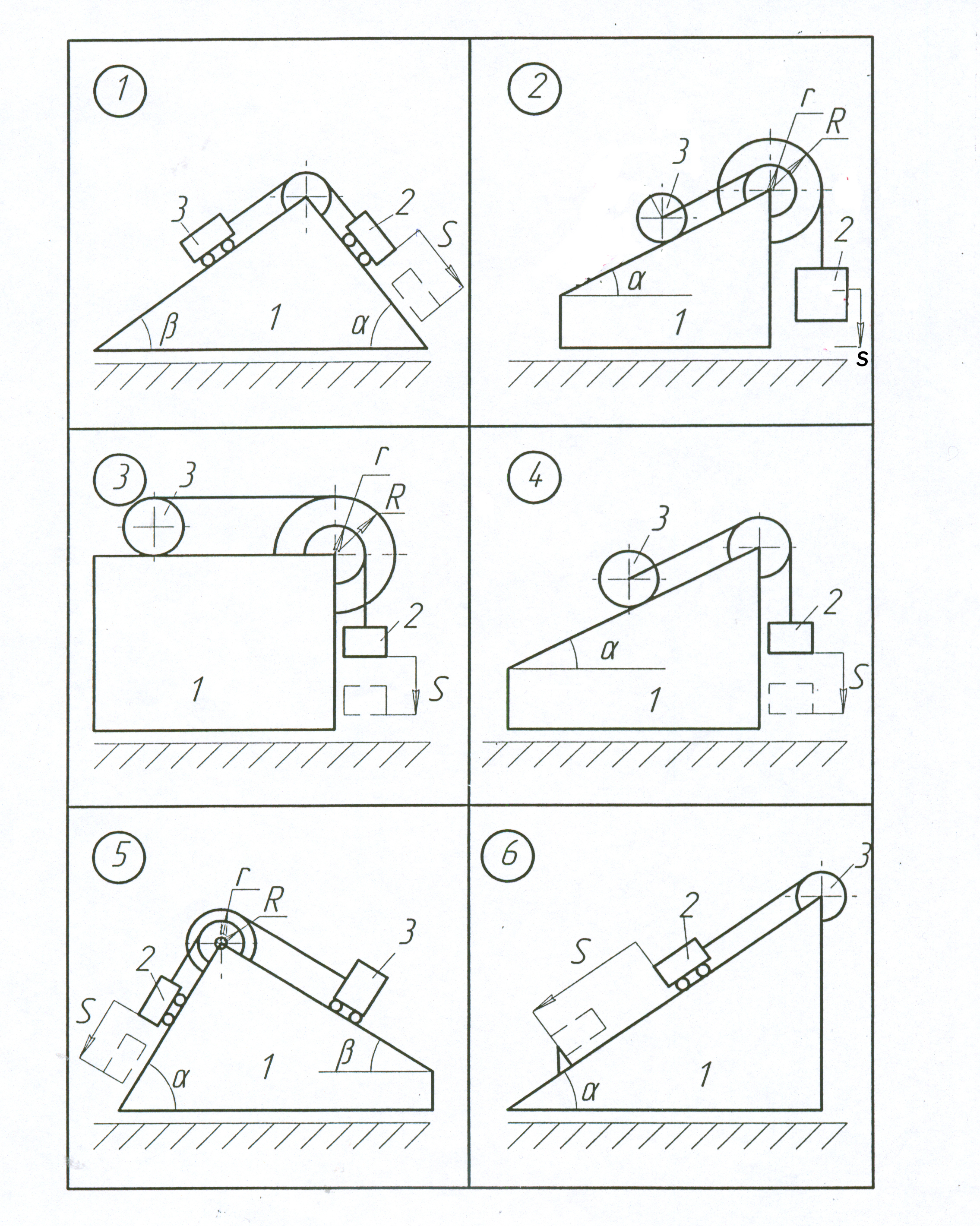 исунок 2.1

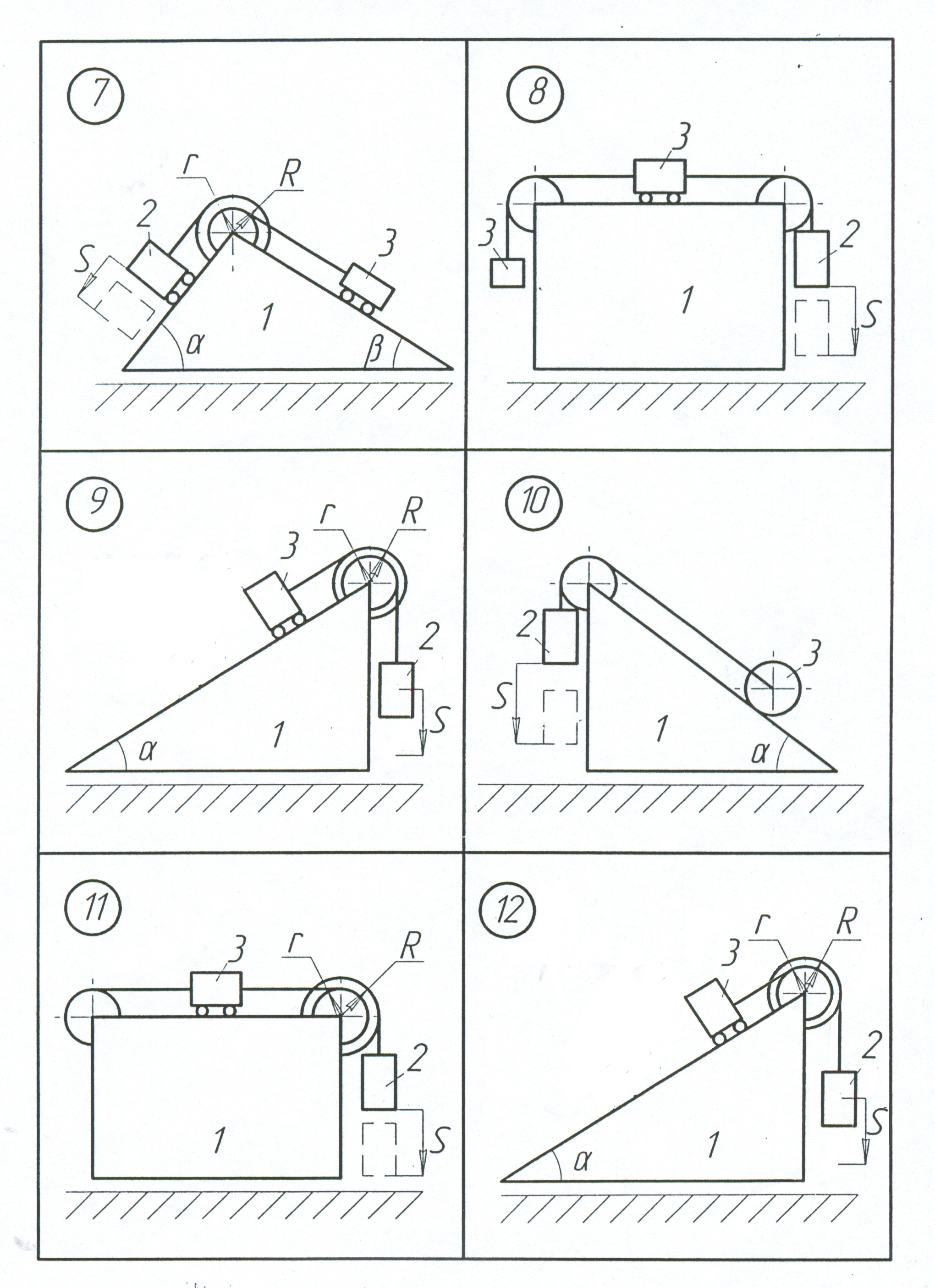
Рисунок 2.2

Рисунок 2.3

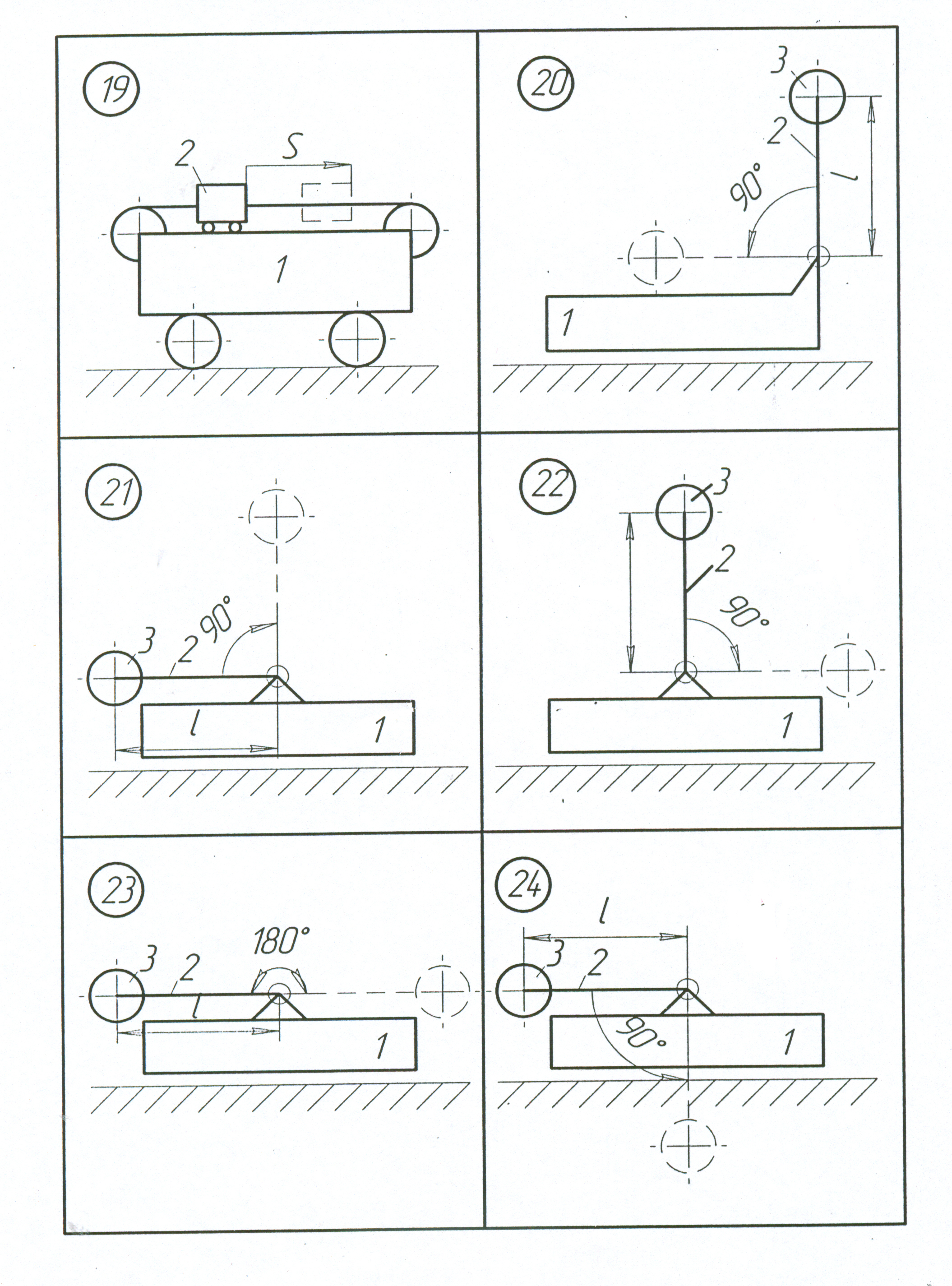
Рисунок 2.4

Р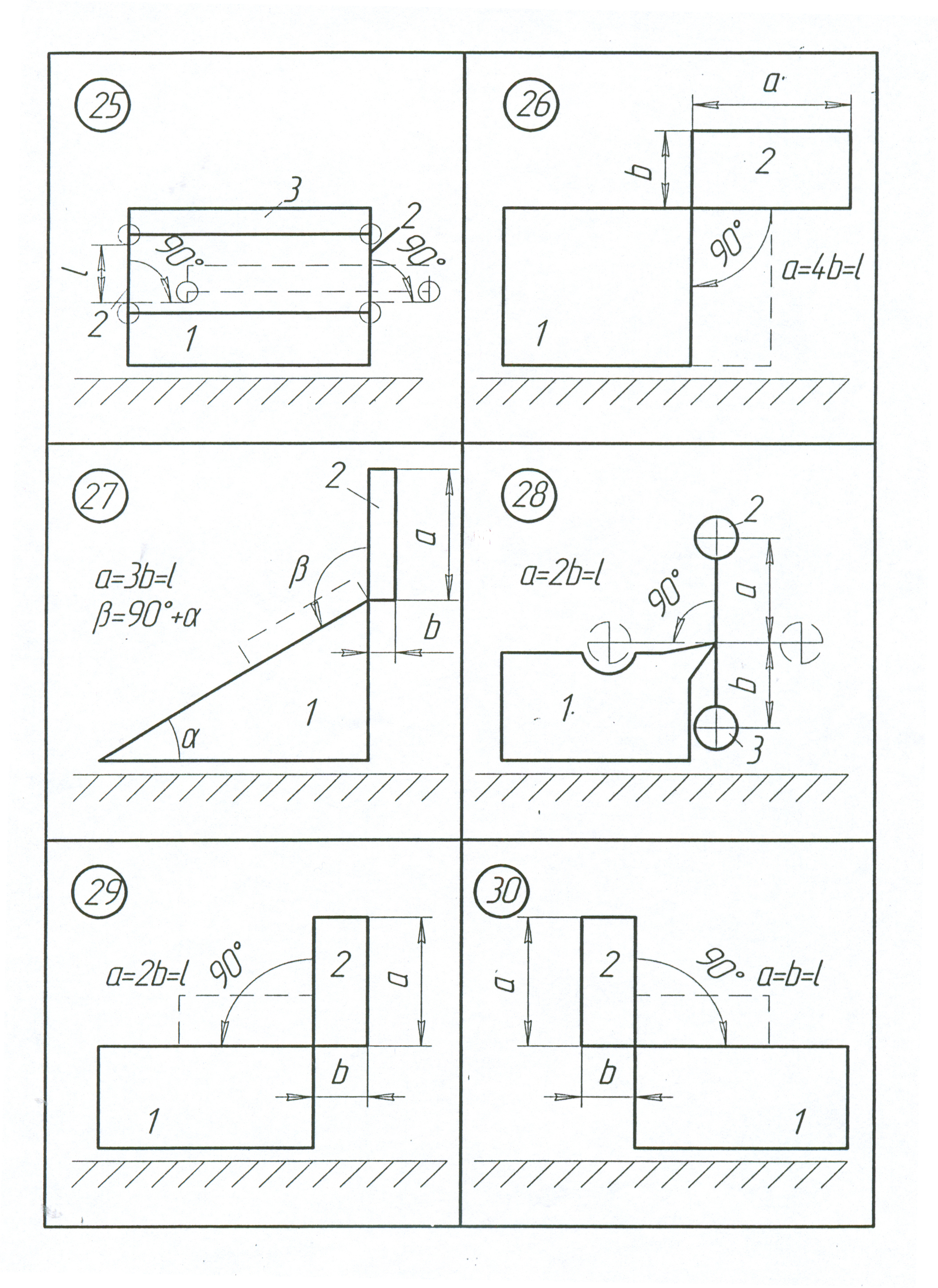 исунок 2.5