Загальне рівняння динаміки

Д.11 Розрахунок характеристик руху механічної системи за допомогою загального рівняння динаміки

Механічна система (рис. 11.1 – 11.5) складається з вантажу 1 масою , двох шківів 2 і 3 з масами і , радіусами ступенів і , і , та радіусами інерції , відповідно і суцільного циліндри-чного катка 4 масою . На шків 2 або 3, діє постійний момент М. Вантаж 1, або каток 4, лежать на гладенькій горизонтальній або похилій площині з кутом нахилу чи до горизонталі. Тертя при русі вантажу 1 і ковзання при кочені катка 4 відсутні. Система розташована в вертикальній площині.

Визначити прискорення вантажу 1 і натяг троса, який до нього закріплений, якщо масою тросів і тертям в підшипниках шківів нехтуємо.

В остаточних розрахунках прийняти значення параметрів з таблиці 11.1 по варіантах.

Таблиця 11.1

В-т	кг				см					град.
					r2	R2	r3	R3	М		
1	5	0	2	3	10	25	18	35	8	15	45
2	15	4	0	10	8	32	20	36	6	30	60
3	12	0	3	8	12	24	15	30	5	45	30
4	8	5	0	2	6	18	4	32	4	600	15
5	14	0	6	4	9	27	10	20	12	45	60
6	6	2	0	3	3	12	6	24	6	15	60
7	20	0	15	8	14	28	15	30	5	45	75
8	10	6	0	5	8	16	8	32	8	30	45
9	16	0	10	6	6	9	16	32	10	15	45
0	18	3	0	12	5	20	8	24	5	45	60

11.1 Приклад виконання завдання

Для механічної системи, яка наведена на рис. 11.6, задано: кг, кг, кг, кг, м, м, м, . Радіус інерції ступінчатого барабана 2 рівний м, коефіцієнт тертя ковзання тіла 3 по горизонтальній площині . Циліндричне тіло 4 котиться по похилій площині без тертя і без ковзання.

Визначити прискорення тіла 1 – , тіла 3 – , натяги тросів N₁ і N₃, до яких ці тіла прикріплені.

Рисунок 11.1

Р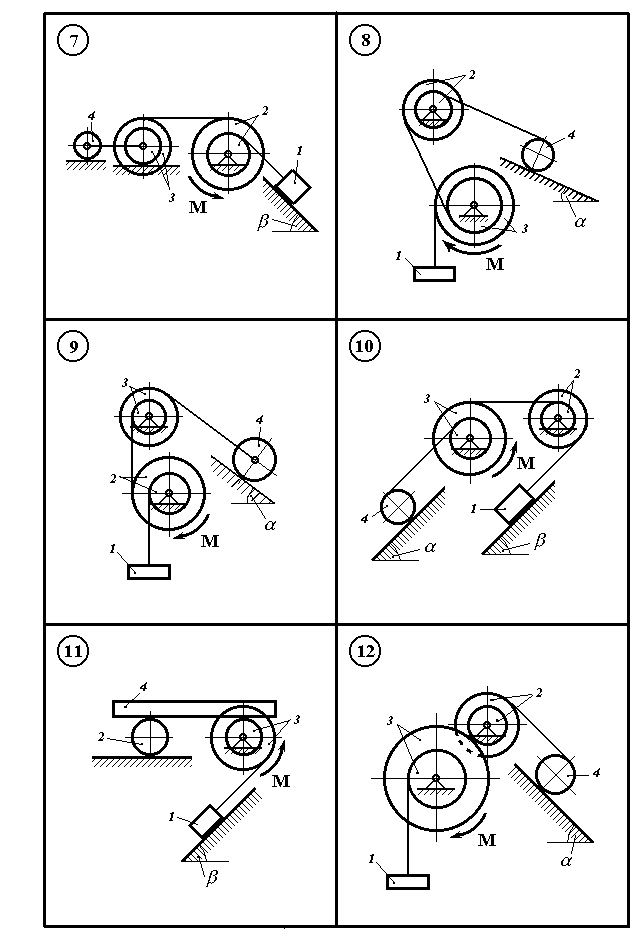 исунок 11.2

Рисунок 11.3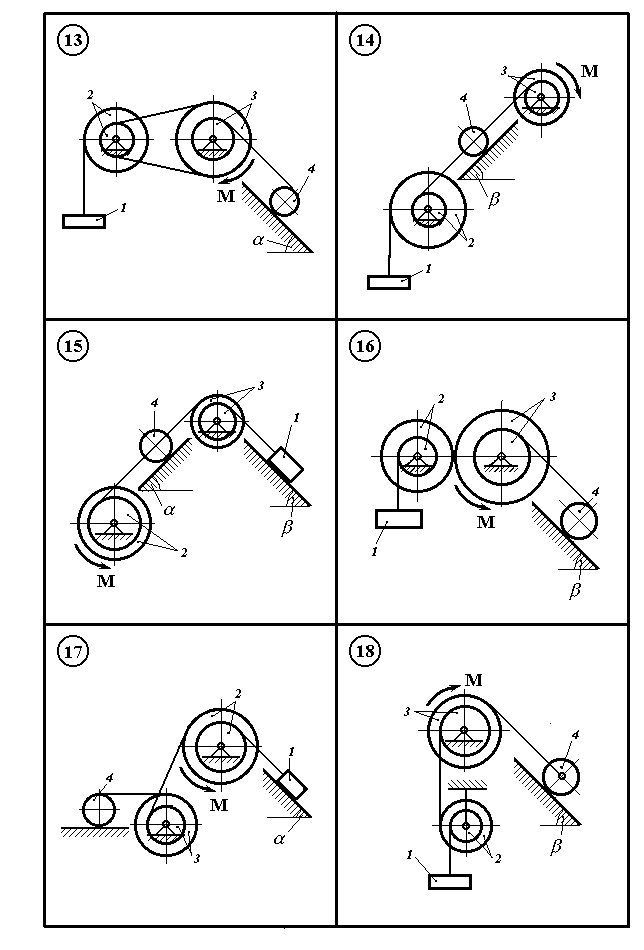

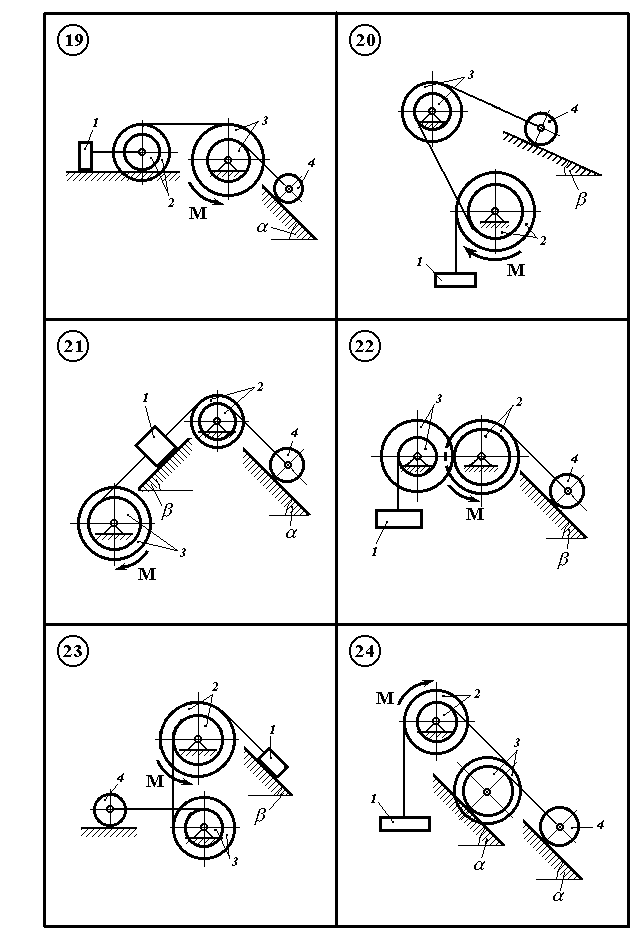
Рисунок 11.4

Р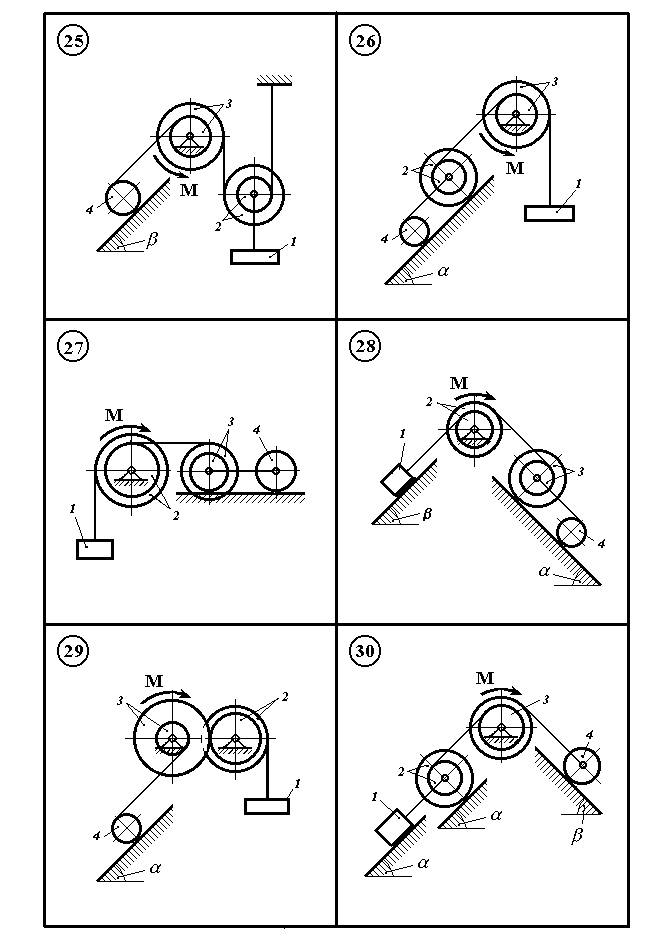 исунок 11.5

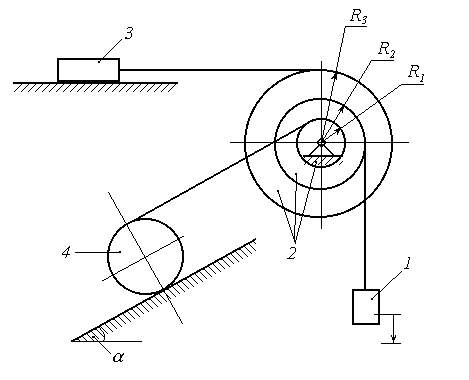
Рисунок 11.6

Розв’язання. Для розв’язування задачі використовуємо загальне рівняння динаміки:

(11.1)

Покажемо для всіх тіл механізму активні сили, напрямки прискорень, інерційні сили і віртуальні переміщення, що зображені на рис. 11.7.

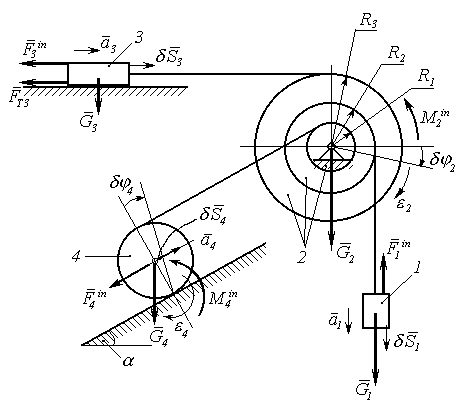
Рисунок 11.7

Активні сили: .

Інерційні сили:

Віртуальні переміщення:

для тіла 1 – , для тіла 2 – , для тіла 3 – , для тіла 4 – і .

Складаємо загальне рівняння динаміки відповідно до формули (11.1).

(11.2)

В рівняння (11.2) не ввійшли сили і тому, що вони роботи не виконують. Виразимо віртуальні переміщення , , і через .

; .

Звідки:

, , , (11.3)

Моменти інерції тіл 2 і 4 відповідно рівні:

, . (11.4)

Знайдемо активні сили:

, , . (11.5)

Знайдемо інерційні сили:

, , , , .

Виразимо кутові прискорення і , а також прискорення і через .

; ,

тому , , .

Тоді інерційні сили матимуть вигляд:

, , ,

. (11.6)

Підставляємо активні сили (11.5), інерційні сили (11.6) і віртуальні переміщення (11.3) в рівняння (11.2)

Після спрощення і скорочення на одержуємо рівняння

звідки

.

Підставимо дані умови:

м/с².

м/с².

Для визначення натягів тросів, що прикріплені до тіл 1 і 3, застосовуємо принцип Даламбера.

Розглянемо сили, які діють на вантаж 1 і покажемо їх на рис. 11.8.

Згідно з принципом Даламбера

.

Проектуємо цю векторну рівність на вісь oy, отримаємо:

.

Звідки

.

Або:

.

Рисунок 11.8

Розглянемо сили, які діють на тіло 3, що зображено на рис. 11.9., на основі

п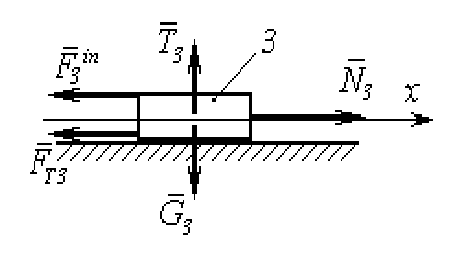 ринципу Даламбера

.

Проектуємо це рівняння на вісь ox.

.

Рисунок 11.9

Звідки:

.

Відповідь: a₁=8.43 м/с², N₃=26.4 н.