14.3 Задача Ляме

Я

Рисунок 14.3

кщо відношення товщини стінки циліндра до внутрішнього радіуса перевищує 1/10, то циліндр слід вважати товстостінним і розраховувати його на основі більш точної теорії. Така задача була вперше розв’язана французьким ученим Г.Ляме. При виборі теорії розрахунку потрібно пам’ятати, що поділ циліндрів на товстостінні і тонкостінні є досить умовним і пов’язаний з необхідною точністю їх розрахунку.

Розглянемо циліндр з внутрішнім і зовнішнім радіусами, що перебуває під дією внутрішнього і зовнішнього тисків (рис. 14.3)

Двома поперечними перерізами на віддалі, що дорівнює одиниці, виділимо з циліндра кільце, яке й надалі будемо розглядати.

Із цього кільця виділимо двома площинами, що проходять через його центр під кутом і двома співвісними циліндричними поверхнями з радіусами і , малий елемент (рис. 14.4,а).

В

Рисунок 14.4

а)

б)

наслідок симетрії грані виділеного елемента не будуть перекошуватися при деформації кільця, тобто будуть головними площадками з головними напруженнями: радіальним і коловим (рис. 14.4,б). Нехай ці напруженням є розтягуючими, причому напруження при переході від циліндра радіу-сом до циліндра радіусом змінюється на .

Розглянемо статичний аспект задачі. З умови рівноваги проекцій зусиль на радіус кільця знаходимо

,

звідки, після нехтування добутком малих величин,

.

(14.9)

Г

Рисунок 14.5

еометричний аспект задачі. Радіальне переміщення довільної точки кільця з абсцисою позначимо через , приріст цього переміщення за рахунок зміни координати на величину буде 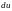(рис. 14.5).

Тоді відносні лінійні деформації у радіальному і тангенціальному напрямках і виражаються через переміщення за формулами:

, .

(14.10)

Фізичний аспект задачі описується рівняннями закону Гука, які після підстановки в них значень відносних деформацій (14.10) розв’язуємо відносно напружень і

(14.11)

Підставляючи вирази для напружень (14.11) у рівняння статики (14.9), після перетворень приходимо до такого диференціального рівняння відносно невідомої

.

(14.12)

Розв’язок цього диференціального рівняння другого порядку зі змінними коефіцієнтами (рівняння Ейлера) має вигляд

.

(14.13)

Підстановка виразу для у рівняння (14.11) приводить до таких виразів для напружень:

Сталі інтегрування і визначаємо з граничних умов на внутрішньому та зовнішньому контурах кільця

, .

Ці умови дають два рівняння:

з яких знаходимо

, .

(14.14)

Таким чином, формули для напружень і радіального переміщення остаточно набирають вигляду

,	(14.15)
.	(14.16)

Із формул для і видно, що їх сума – величина стала, тобто

Тому і відносна лінійна деформація кільця у напрямку осі циліндра – величина стала

.

Якщо при наявності днищ у циліндрі виникає паралельна до його осі поздовжня сила , то в його поперечних перерізах виникають напруження

,

(14.17)

а до виразу (14.16) для переміщення додається доданок

.

(14.18)

З погляду практичних розрахунків найбільш цікавим є випадок навантаження товстостінного циліндра лише внутрішнім тиском .

Тоді та і вирази для напружень (14.15) спрощуються

.

(14.19)

Епюри і для цього випадку показані на рис. 14.6. Напруження - розтягуючі, - стискуючі. Екстремальні значення цих напружень виникають на внутрішньому контурі циліндра, вони є найбільшим і найменшим головними напруженнями

, ,

де .

Я

Рисунок 14.6

кщо розтягуючих зусиль вздовж осі циліндра немає, тоді середнє головне напруження дорівнює нулю . Якщо такі зусилля є, тоді .

Перевірку міцності циліндра слід виконати за однією з теорій міцності залежно від властивостей матеріалу.

Припустимо, матеріал пластичний, тоді за третьою теорією міцності ,

або .

(14.20)

Якщо потрібно підібрати розміри циліндра, то, задаючись величиною одного з радіусів і відношенням , можна з формули (14.20) визначити необхідну величину другого радіуса циліндра.

З формули (14.20) видно, що навіть при відношенні (зовнішній радіус циліндра безмежно великий), ми не можемо допустити в циліндрі тиску більше ніж .

Отже, збільшення зовнішнього радіуса циліндра при великих товщинах його стінки дає незначний ефект щодо підвищення його міцності.

55