- •Билет №1 Интерференция световых волн. Когерентность световых волн. Условие мах. И мин. Для интерференции света. Оптическая длина пути.
- •Опыт Юнга
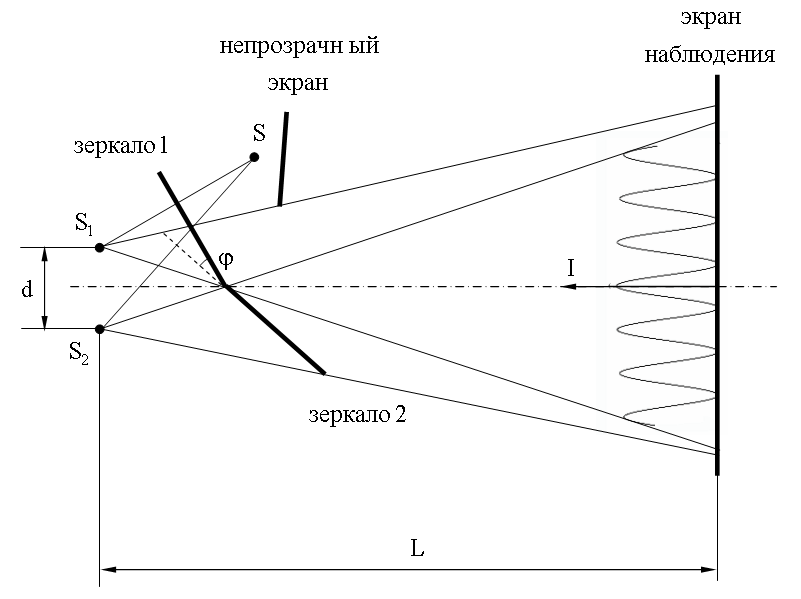
- •Зеркала Френеля
- •Бипризма Френеля
- •Интерференция света в тонких пленках. Полосы равного наклона и равной толщины.
- •Билет №5 Кольца Ньютона. Способ их наблюдения. Радиусы колец.
- •Интерферометры. Интерферометр Майкельсона. Применение интерферометров.
- •Дифракция света. Принцип Гюйгенса и Гюйгенса-Френеля. Метод зон Френеля. Прямолинейное распространение света.
- •Билет 8 Дифракция Френеля на круглом отверстии:
- •Билет №9 дифракция фраунгофера на одной щели.
- •Билет№10
- •Билет № 11 Дифракционная решетка как спектральный прибор. Угловая и линейная дисперсия. Разрешающая способность.
- •3. 7. Дисперсия и разрешающая сила спектрального прибора. @
- •Билет 13 Понятие о голографии. Получение и восстановление голографических снимков. Особенности голографического снимка.
- •Билет 14
- •Вопрос 18
- •Вопрос 19. Вращение плоскости поляризации света. Оптический активные вещества.
- •Вопрос 20 Магнитное вращение плоскости поляризации
- •Вопрос 21 Искусственная оптическая поляризация. Эффект Керра и Коттона- Мутона.
- •Вопрос 22 Поглощение света при прохождении через вещество. Механизм поглощения.
- •Вопрос 23 Рассеяние света в веществе.
- •Вопрос 24 Дисперсия света в веществе. Нормальная и аномальная дисперсия. Объяснение дисперсии света.
- •Вопрос 25 Эффект Вавилова- Черенкова.
- •Вопрос 26
- •Впорс 27 Связь между лучеиспускательной и поглащательной способностями тел.
- •Вопрос 28 Распределение световой энергии в спектре абсолютно- черного тела. Серые тела.
- •Вопрос 29 Теория Релея и Джинса. Затруднения классической теории излучения.
- •Вопрос 30 Квантовая гипотеза Планка. Энергия светвого кванта. Функция распределения Планка.
- •Вопрос 31
- •Вопрос 32
- •Вопрос 33
- •Вопрос 34
- •Вопрос 35
- •Вопрос 36
- •Вопрос 37
- •Вопрос 38
- •Вопрос 39
- •Вопрос 40
- •Вопрос 41
- •Вопрос 42
- •Вопрос 43
- •Вопрос 45 Частица в одномерной потенциальной яме. Квантование энергии.
- •Вопрос 46
- •Вопрос 47
- •Вопрос 48
- •Вопрос 49
- •Вопрос 50 Периодическая система химических элементов - естественная классификация химических элементов, являющаяся табличным выражением периодического закона д.И. Менделеева.
Билет №1 Интерференция световых волн. Когерентность световых волн. Условие мах. И мин. Для интерференции света. Оптическая длина пути.
Если монохроматические световые волны имеют постоянную во времени разность фаз и колебания их световых векторов происходят в одной плоскости, то они называются когерентными (от греч. cohereus - согласованный). Т.е Когерентные волны - это волны, испускаемые источниками, имеющими одинаковую частоту и постоянную разность фаз. Такие согласованные когерентные волны при наложении их друг на друга могут создать в пространстве картину, заключающуюся в чередовании светлых и темных областей. Данное явление перераспределения интенсивности световой волны в пространстве при наложении двух или нескольких когерентных волн называется интерференцией света.
Амплитуда
может принимать нулевое значение, если
![]() а это выполняется если аргумент
косинуса равен нечетному числу π/2. При
этом происходит взаимное «гашение»
волн и мы наблюдаем ослабление
интенсивности суммарной волны, то есть
интерференционный
минимум.
Таким образом, если в произвольной точке
пространства оптическая разность хода
накладываемых волн равна нечетному
числу полуволн, то в ней наблюдается
минимум интерференции. Условие
а это выполняется если аргумент
косинуса равен нечетному числу π/2. При
этом происходит взаимное «гашение»
волн и мы наблюдаем ослабление
интенсивности суммарной волны, то есть
интерференционный
минимум.
Таким образом, если в произвольной точке
пространства оптическая разность хода
накладываемых волн равна нечетному
числу полуволн, то в ней наблюдается
минимум интерференции. Условие
![]() (m=0,1,2…)есть
условие
интерференционного минимума.
Если в
произвольной точке пространства
оптическая разность хода накладываемых
волн равна четному числу полуволн или
целому числу длин волн, то в ней наблюдается
максимум интерференции и условие
(m=0,1,2…)есть
условие
интерференционного минимума.
Если в
произвольной точке пространства
оптическая разность хода накладываемых
волн равна четному числу полуволн или
целому числу длин волн, то в ней наблюдается
максимум интерференции и условие
![]() (m=0,1,2…)
является условием
интерференционного максимума.
Если между световыми волнами существует
разность хода, то они также обладают
разностью фаз.
(m=0,1,2…)
является условием
интерференционного максимума.
Если между световыми волнами существует
разность хода, то они также обладают
разностью фаз.
Получим условия интерференционных максимумов и минимумов для разности фаз δ:
![]() .
.
Если вместо Δ подставить значения Δmax и Δ min, то мы получим условия максимума и минимума интерференции для разности фаз δ max = ±2πm и δ min = ±(2m+1)π, ( m = 0,1,2…).
ОПТИЧЕСКАЯ ДЛИНА
ПУТИ между
точками А и В прозрачной
среды - расстояние, на которое свет
распространился бы в вакууме за то же
время, за какое он проходит от А до В в
среде
(путь,
который прошел бы свет за
то же время,
распространяясь в вакууме). Поскольку
скорость света в любой среде меньше его
скорости в вакууме,
О. д. п. всегда больше реально проходимого
расстояния (в предельном случае вакуума
равна ему). В оптич. системе, состоящей
из р однородных
сред (траектория луча света в такой
системе - ломаная линия), О. д. п. равна
сумме![]() где lk -
расстояние, пройденное светом в k-й
среде (k -
1, 2,..,), nk -
показатель преломления этой среды. В
среде с плавно меняющимся п(1)(траектория
луча в такой среде - кривая линия) О. д.
п. есть
где lk -
расстояние, пройденное светом в k-й
среде (k -
1, 2,..,), nk -
показатель преломления этой среды. В
среде с плавно меняющимся п(1)(траектория
луча в такой среде - кривая линия) О. д.
п. есть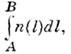 где dl -
бесконечно малый элемент траектории
луча. Понятие "О. д. п." играет большую
роль в оптике, особенно в геометрической
оптике и кристаллооптике,
позволяя сопоставлять пути, проходимые
светом в средах, в к-рых скорости его
распространения различны. Геом. место
точек, для к-рых О. д. п., отсчитываемая
от одного источника, одинакова, наз.
поверхностью световой волны; световые
колебания на этой поверхности находятся
в одинаковой фазе. О. д. п. луча света
между двумя произвольными точками
пространства предметов и пространства
изображений наз. эйконалом.
где dl -
бесконечно малый элемент траектории
луча. Понятие "О. д. п." играет большую
роль в оптике, особенно в геометрической
оптике и кристаллооптике,
позволяя сопоставлять пути, проходимые
светом в средах, в к-рых скорости его
распространения различны. Геом. место
точек, для к-рых О. д. п., отсчитываемая
от одного источника, одинакова, наз.
поверхностью световой волны; световые
колебания на этой поверхности находятся
в одинаковой фазе. О. д. п. луча света
между двумя произвольными точками
пространства предметов и пространства
изображений наз. эйконалом.
Билет №2
Расчет интерференционной картины от двух когерентных источников света. Расстояние между интерференционными полосами и ширина интерференционной полосы.
П усть
в некоторую точку А одновременно приходят
две световые волны от когерентных
источников света S1
и S2,
световые векторы которых колеблются
в одной плоскости (рис.). Пусть источники
начинают излучать одновременно, начальные
фазы волн равны нулю и амплитуды
одинаковы. Тогда уравнения волн можно
записать следующим образом:
усть
в некоторую точку А одновременно приходят
две световые волны от когерентных
источников света S1
и S2,
световые векторы которых колеблются
в одной плоскости (рис.). Пусть источники
начинают излучать одновременно, начальные
фазы волн равны нулю и амплитуды
одинаковы. Тогда уравнения волн можно
записать следующим образом:

Складывая эти выражения, можно получить что результирующая величина Е в точке А будет равна:
![]() .
.
Величина
![]() не
зависит от времени и является амплитудой
суммарного колебания в точке А. Амплитуда
может принимать нулевое значение, если
а это выполняется если аргумент
косинуса равен нечетному числу π/2. При
этом происходит взаимное «гашение»
волн и мы наблюдаем ослабление
интенсивности суммарной волны, то есть
интерференционный
минимум.
Таким образом, если в произвольной точке
пространства оптическая разность хода
накладываемых волн равна нечетному
числу полуволн, то в ней наблюдается
минимум интерференции. Условие
есть условие
интерференционного
минимума.
Если в
произвольной точке пространства
оптическая разность хода накладываемых
волн равна четному числу полуволн или
целому числу длин волн, то в ней наблюдается
максимум интерференции и условие
не
зависит от времени и является амплитудой
суммарного колебания в точке А. Амплитуда
может принимать нулевое значение, если
а это выполняется если аргумент
косинуса равен нечетному числу π/2. При
этом происходит взаимное «гашение»
волн и мы наблюдаем ослабление
интенсивности суммарной волны, то есть
интерференционный
минимум.
Таким образом, если в произвольной точке
пространства оптическая разность хода
накладываемых волн равна нечетному
числу полуволн, то в ней наблюдается
минимум интерференции. Условие
есть условие
интерференционного
минимума.
Если в
произвольной точке пространства
оптическая разность хода накладываемых
волн равна четному числу полуволн или
целому числу длин волн, то в ней наблюдается
максимум интерференции и условие
![]() является условием
интерференционного максимума.
Если между световыми волнами существует
разность хода(∆=L2-L1,
L-оптическая
длина пути; разность оптических длин
проходимых волнами путей- назыв.
оптической разностью хода), то они также
обладают разностью фаз.
является условием
интерференционного максимума.
Если между световыми волнами существует
разность хода(∆=L2-L1,
L-оптическая
длина пути; разность оптических длин
проходимых волнами путей- назыв.
оптической разностью хода), то они также
обладают разностью фаз.
Получим условия интерференционных максимумов и минимумов для разности фаз δ:
.
Если вместо Δ подставить значения Δmax и Δ min, то мы получим условия максимума и минимума интерференции для разности фаз δ max = ±2πm и δ min = ±(2m+1)π, ( m = 0,1,2…).
Ширина
интерференционной полосы-
расстояние между соседними
максимумами или минимумами интенсивности,
равно
![]() ,
, ![]() не зависит от порядка интерференции(
величины m)
и явл. постоянной для данных l,
d,
и
не зависит от порядка интерференции(
величины m)
и явл. постоянной для данных l,
d,
и ![]() .
Согласно формуле,
.
Согласно формуле,![]() обратно пропорционально d;
следов. , при большом расстоянии между
источниками, например при d≈l
обратно пропорционально d;
следов. , при большом расстоянии между
источниками, например при d≈l
Билет№3
Способы наблюдения интерференции света. Метод Юнга, зеркала и бипризма Френеля.
Для осуществления интерференции света необходимо получить когерентные световые пучки, для чего применяются различные приемы.
Когерентные световые волны можно получить, если свет, идущий от одного источника, разделить на две (или более) части и затем заставить их встретиться. В силу общности своего происхождения полученные лучи должны быть когерентными и при наложении интерферировать. Такое разделение может быть осуществлено с помощью экранов и щелей (метод Юнга), зеркал (зеркала Френеля) и преломляющих тел (бипризма Френеля).
1) Т.Юнг с помощью двух щелей получил на экране интерференционную картину. Его опыт заключался в следующем: источником света служила ярко освещенная щель S, от которой световая волна падала на две узкие равноудаленные щели S1 и S2, параллельные S. Щели S1 и S2 можно считать когерентными источниками света, а все три упомянутые щели можно рассматривать как точечные источники, свет от которых распространяется во всех направлениях. Волны, идущие от S1 и S2, накладываясь друг на друга, интерферируют. Интерференционная картина наблюдается на экране Э.
Обозначим
расстояние между щелями S1
и S2
равным d,
а между щелями и экраном - l,
причем l
»
d
(рис. 2.3 а).
Точка О – центр экрана, она расположена
симметрично относительно щелей S1
и S2.
Результат интерференции волн в
произвольной точке экрана М, находящейся
на расстоянии х от его центра О, должен
определяться разностью хода Δ
= l2-
l1.
Математический расчет дает для разности
хода Δ
= хd/l.
В тех местах экрана, которые
удовлетворяют условию
,
образуется интерференционный максимум.
Отсюда
![]()
.
В тех местах экрана, где
,
волны “гасят” друг друга и образуется
интерференционный минимум. Отсюда
тех местах экрана, где
,
волны “гасят” друг друга и образуется
интерференционный минимум. Отсюда
![]() .
.
2) Зеркала Френеля