
- •Лекция 26 Квантовая статистика
- •1. Понятие о квантовой статистике
- •2. Фазовое пространство. Функция распределения
- •3. Функция распределения Бозе – Эйнштейна
- •4. Функция распределения Ферми – Дирака Эта функция определяется аналогично функции распределения Бозе – Эйнштейна и имеет такой вид:
- •5. Понятие о вырождении систем частиц, описываемых квантовыми статистиками
- •Понятие о вырождении электронного газа в металлах
- •6. Квантовая теория теплоемкости. Фононы
3. Функция распределения Бозе – Эйнштейна
Функцией распределения
Бозе – Эйнштейна
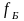 называется середняя
"заселенность" бозонами состояний
с данной энергией, то есть среднее число
частиц в одном состоянии:
называется середняя
"заселенность" бозонами состояний
с данной энергией, то есть среднее число
частиц в одном состоянии:
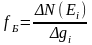 ,
,
где
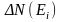 – число частиц с энергией в интервале
от
– число частиц с энергией в интервале
от
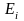 до
до
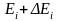 ;
;
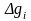 – число квантовых состояний в этом
интервале энергий.
– число квантовых состояний в этом
интервале энергий.
Для
нахождения функции
рассматривается термодинамическая
вероятность Р
распределения частиц системы по
квантовым состояниям и находится самое
вероятное роспределение при условии
сохранения числа частиц
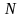 в системе и энергии
в системе и энергии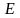 системы:
системы:
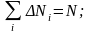
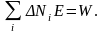
Суммирование проводится по всем квантовым состояниям системы.
Применяя метод неопределенных множителей Лагранжа при отыскании условного экстремума, можно получить такое выражение для функции распределения Бозе — Эйнштейна:
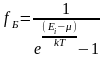 ,
,
где
– среднее число частиц (бозонов) в
квантовом состоянии
с энергией
;
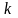 – постоянная Больцмана; Т
— абсолютная температура;
– постоянная Больцмана; Т
— абсолютная температура;
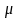 – химический потенциал, который не
зависит от энергии, а определяется
только лишь температурой и плотностью
числа частиц.
– химический потенциал, который не
зависит от энергии, а определяется
только лишь температурой и плотностью
числа частиц.
4. Функция распределения Ферми – Дирака Эта функция определяется аналогично функции распределения Бозе – Эйнштейна и имеет такой вид:
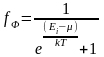 ,
,
где
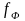 – среднее число частиц (фермионов) в
квантовом состоянии
с энергией
;
– химический потенциал, который, в
отличие от химического потенциала,
входящего в функцию распределения Бозе
– Эйнштейна , может иметь положительное
значение.
– среднее число частиц (фермионов) в
квантовом состоянии
с энергией
;
– химический потенциал, который, в
отличие от химического потенциала,
входящего в функцию распределения Бозе
– Эйнштейна , может иметь положительное
значение.
Если
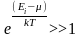 ,
то распределения Бозе – Эйнштейна и
Ферми — Дирака переходят в классическое
распределение Максвелла – Больцмана:
,
то распределения Бозе – Эйнштейна и
Ферми — Дирака переходят в классическое
распределение Максвелла – Больцмана:
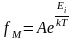 ,
,
где
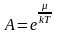 .
.
Таким образом, при высоких температурах оба "квантованных" газа ведут себя подобно классическому газу.
5. Понятие о вырождении систем частиц, описываемых квантовыми статистиками
Система частиц (в частности, идеальный газ) называется вырожденной, если ее свойства существено отличаются от свойств систем, подчиняющихся законам классической статистики. Отступлении в поведении бозе- и ферми-газов от классического максвелл-больцмановского газа называется вырождением газов (вырожденный газ). Вырождение газов становится существенным при очень низких температурах и большой плотности.
Параметром вырождения называется величина .
Температурой
вырождения
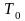 называется температура, ниже которой
четко проявляются квантовые свойства
идеального газа, обусловленные
тождественностью частиц, то есть
– это температура, при которой вырождение
становится существенным. Если
называется температура, ниже которой
четко проявляются квантовые свойства
идеального газа, обусловленные
тождественностью частиц, то есть
– это температура, при которой вырождение
становится существенным. Если
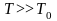 ,
то поведение системы частиц (газа)
описывается классическими законами.
,
то поведение системы частиц (газа)
описывается классическими законами.
Понятие о вырождении электронного газа в металлах
Распределение электронов по разным квантовым состояниям подчиняется принципу Паули, согласно с которым в одном состоянии не может быть двух одинаковых (с однаковым набором четырех квантовых чисел) электронов; они должны отличаться какой-то характеристикой, например, направлением спина. Итак, согласно квантовой теории, электроны в металле не могут размещаться на самом низком энергетическом уровне даже при 0 К. Согласно принципу Паули, электроны вынужденны подниматься вверх по " энергетическим ступенькам".
Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми – Дирака
,
Если
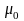 – химический потенциал электронного
газа при
– химический потенциал электронного
газа при
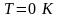 ,
то среднее число
,
то среднее число
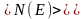 электронов в квантовом состоянии с
энергией Е равно
электронов в квантовом состоянии с
энергией Е равно
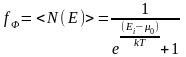 .
.
Для фермионов
(а электроны являються фермионами)
среднее число частиц в квантовом
состоянии и вероятность заселения
квантового состояния совпадают, поскольку
квантовое состояние може быть или не
заселено, или в нем будет находиться
одна частица. Это означает, что для
фермионов
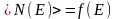 ,
где
,
где
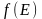 – функция распределения электронов по
состояниям.
– функция распределения электронов по
состояниям.
Из выше приведенной формулы
следует, что при
функция распределения
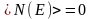 ,
если
,
если
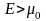 .
График этой функции приведен на рис.
26.1, а. В области энергий
от 0 до
функция
равна единице. При
.
График этой функции приведен на рис.
26.1, а. В области энергий
от 0 до
функция
равна единице. При
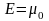 она скачкообразно изменяется до нуля.
Это значит, что при
все
нижние квантовые состояния, вплоть до
состояния с энергией
заполнены электронами, а все состояния
с энергией, большей
,
свободны. Значит,
- не что иное, как максимальная
кинетическая энергия, которую могут
иметь электроны проводимости в металле
при
.
Эта максимальная кинетическая энергия
называєтся энергиею
Ферми и обозначается
она скачкообразно изменяется до нуля.
Это значит, что при
все
нижние квантовые состояния, вплоть до
состояния с энергией
заполнены электронами, а все состояния
с энергией, большей
,
свободны. Значит,
- не что иное, как максимальная
кинетическая энергия, которую могут
иметь электроны проводимости в металле
при
.
Эта максимальная кинетическая энергия
называєтся энергиею
Ферми и обозначается
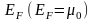 .
Потому распределение Ферми – Дирака
обычно записывается в виде
.
Потому распределение Ферми – Дирака
обычно записывается в виде
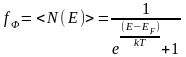 .
.
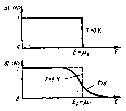
Рис. 26.1
Самый высокий энергетический
уровень, занятый электронами, называется
уровнем Ферми.
Уровню Ферми отвечает энергия Ферми
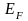 ,
которую имеют электроны на этом уровне.
Уровень Ферми, очевидно, будет тем выше,
чем больше плотность электронного газа.
Работу выходу электрона из металла
нужно отсчитывать не от дна "потенциальной
ямы", как в классической теории, а от
уровня Ферми, то есть от верхнего из
занятых электронами энергетических
уровней.
,
которую имеют электроны на этом уровне.
Уровень Ферми, очевидно, будет тем выше,
чем больше плотность электронного газа.
Работу выходу электрона из металла
нужно отсчитывать не от дна "потенциальной
ямы", как в классической теории, а от
уровня Ферми, то есть от верхнего из
занятых электронами энергетических
уровней.
Для металлов при не очень
высоких температурах выполняется
неравенство
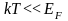 .
Это означает, что
электронный газ в металлах практически
всегда находится в состоянии сильного
вырождения. Температура
вырождения определяется из условия
.
Это означает, что
электронный газ в металлах практически
всегда находится в состоянии сильного
вырождения. Температура
вырождения определяется из условия
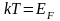 .
Она определяет предел,
выше которого квантовые эффекты перестают
быть существенными. Соответственные
расчеты показывают, что для электронов
в металле
.
Она определяет предел,
выше которого квантовые эффекты перестают
быть существенными. Соответственные
расчеты показывают, что для электронов
в металле
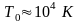 ,
то есть для всех температур, при которых
металл может существовать в твердом
состоянии, электронный газ в металле
- вырожденный.
,
то есть для всех температур, при которых
металл может существовать в твердом
состоянии, электронный газ в металле
- вырожденный.
При температурах, отличных
от
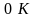 ,
функция распределения Ферми –Дирака
плавно изменяется от 1 до 0 в узкой области
(порядка кТ) в
окрестности EF
(рис. 26.1, б).
(Тут же для сравнения
пунктиром приведена функция распределения
при
.)
Это объясняется
тем, что при Т
> 0 небольшое количество электронов с
энергией, близкой к
,
возбуждается вследствие теплового
движения и их энергия
становится больше, чем
.
Вблизи предела Ферми
при
,
функция распределения Ферми –Дирака
плавно изменяется от 1 до 0 в узкой области
(порядка кТ) в
окрестности EF
(рис. 26.1, б).
(Тут же для сравнения
пунктиром приведена функция распределения
при
.)
Это объясняется
тем, что при Т
> 0 небольшое количество электронов с
энергией, близкой к
,
возбуждается вследствие теплового
движения и их энергия
становится больше, чем
.
Вблизи предела Ферми
при
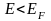 заполнение электронами меньше единицы,
а при
–
больше нуля. В тепловом
движении принимает участие только
небольшое число электронов,
например,
при комнатной температуре
заполнение электронами меньше единицы,
а при
–
больше нуля. В тепловом
движении принимает участие только
небольшое число электронов,
например,
при комнатной температуре
 и
температуре вырождения
и
температуре вырождения
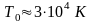 ,
— это 10-5
от общего числа электронов.
,
— это 10-5
от общего числа электронов.
Если
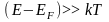 ("хвост" функции распределения),
то единицей в знаменателе функции
распределения Ферми –Дирака можно
пренебречь в сравнении с экспонентой
и тогда распределение Ферми — Дирака
переходит в распределение
Максвелла – Больцмана.
Таким образом, при
,
то есть при больших значенниях
энерии, к электронам в
металле применима классическая
статистика, в то же время, когда
("хвост" функции распределения),
то единицей в знаменателе функции
распределения Ферми –Дирака можно
пренебречь в сравнении с экспонентой
и тогда распределение Ферми — Дирака
переходит в распределение
Максвелла – Больцмана.
Таким образом, при
,
то есть при больших значенниях
энерии, к электронам в
металле применима классическая
статистика, в то же время, когда
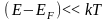 ,
к ним можно применять только квантовую
статистику Ферми –
Дирака.
,
к ним можно применять только квантовую
статистику Ферми –
Дирака.
