7

Лекция 26 Квантовая статистика

1. Понятие о квантовой статистике

Квантовой статистикой называется статистический метод исследования, который применяется к системам, состоящих из большого числа частиц и подчиняющимся законам квантовой механики.

В отличие от начальных положений классической статистической физики квантовая статистика базируется на принципе неразличимости тождественных частиц: все одинаковые частицы (например, все еэлектроны в металлах, все протоны в ядрах атомов) считаются принципиально неотличимыми друг от друга. Таким образом, в квантовой механике одинаковые частицы теряют свою индивидуальность.

Тождественные частицы экспериментально различить невозможно. Этот принцип – не просто следствие интерпретации достоверности волновой функции; он вводится в квантовую механику как новый фундаментальный принцип.

Учитывая физическое значение квадрата модуля волновой функции , принцип неразличимости тождественных частиц можно записать в виде

,

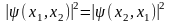где і – соответственно совокупность пространственных и спиновых координат первой и второй частиц. Таким образом, возможны два случая:

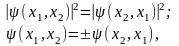
то есть принцип неразличимости тождественных частиц приводит к определенному свойству симметрии волновой функции.

Симметричная волновая функция – это волновая функция, которая при обмене частиц местами не изменяет знак.

Антисимметрична волновая функция – это волновая функция, которая при обмене частиц местами изменяет знак.

Изменение знака волновой функции не означает изменения состояния, поскольку физическое значение имеет только квадрат модуля волновой функции. Частицы с полуцелым спином (например, электроны, протоны, нейтроны) описываются антисимметрическими волновыми функциями и подчиняются статистике Ферми – Дирака; эти частицы называют фермионами. Частицы с нулевым или целочисленным спином (например, -мезоны, фотоны) описываются симметрическими волновыми функциями и подчиняются статистике Бозе – Эйнштейна; эти частицы называют бозонами. Сложные частицы (например, атомные ядра), состоящие из нечетного числа фермионов, являются фермионами (суммарный спин – полуцелый), а из четного – бозонами (суммарный спин целый).

2. Фазовое пространство. Функция распределения

        Пусть система состоит из N частиц. Рассмотрим многомерное пространство всех координат и импульсов частиц системы. Тогда состояние системы определяется заданными 6N переменными, т.к. состояние каждой частицы определяется тремя координатами (x, y, z) и тремя соответствующими проекциями импульсов (p_x, p_y, p_z). Соответственно число “взаимно перпендикулярных” координатных осей данного пространства равно 6N. Это 6N-мерное пространство называется фазовым пространством. Каждому микросостоянию системы отвечает точка в 6N-мерном фазовом пространстве, т.к. задание точки фазового пространства означает задание координат и импульсов всех частиц системы. Разобьем фазовое пространство на малые 6N-мерные элементарные ячейки объемом dqdp = dq₁ dq₂ … dq₃N dp₁ dp₂ … dp₃N, где q - совокупность координат всех частиц; p - cовокупность проекций их импульсов. Корпускулярно-волновой дуализм свойств вещества и соотношение неопределенностей Гейзенберга приводят к выводу, что объем элементарной ячейки, который называется фазовым объемом, не может быть меньше, чем h³, где h - постоянная Планка.

        Вероятность dW данного состояния системы можно представить с помощью функции распределения f(q, p):

dW = f(q, p) dqdp.

        Здесь dW - вероятность того, что точка фазового пространства попадет в элемент фазового объема dqdp, расположенного вблизи данной точки q, p. Иными словами, dW представляет собой вероятность того, что система находится в состоянии, в котором ее координаты и импульсы заключены в интервале q, q + dq и p, p + dp.

       Функция распределения есть не что иное, как плотность вероятности определенного состояния системы. Поэтому она должна быть нормирована:

,

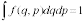где интегрирование производится по всему фазовому пространству.

  Зная функцию распределения f(q, p), можно решить основную задачу квантовой статистики, которая заключается в определении средних значений величин, характеризующих рассматриваемую систему. Среднее значение любой функции таково:

.

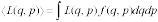        Если иметь дело не с координатами и импульсами, а с энергией, которая квантуется, то состояние системы характеризуется не непрерывной, а дискретной функцией распределения.

        Явное выражение функции распределения в самом общем виде получил американский физик Д.Гиббс. Она называется каноническим распределением Гиббса. В квантовой статистике каноническое распределение Гиббса имеет следующий вид:

,

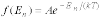где A - постоянная, определяемая из условия нормировки; n - совокупность всех квантовых чисел, характеризующих данное состояние. Необходимо отметить, что f(E_n) есть именно вероятность данного состояния, а не вероятность того, что система имеет определенное значение энергии E_n, т.к. данной энергии может соответствовать не одно, а несколько различных состояний.