Алгоритм Диффи-Хеллмана. Открытое распределение ключей.

Алгоритм, позволяющий двум сторонам получить общий секретный ключ, используя незащищенный от прослушивания, но защищённый от подмены, канал связи. Этот ключ может быть использован для шифрования дальнейшего обмена с помощью алгоритма симметричного шифрования.

Все абоненты открытой сети знают пару открытых ключей: общий ключ P (случайное простое число) и q<P – образующий по модулю P (первообразный корень) – число, которое возведенное последовательно в степень дает все числа, меньшие p и больше 0.Если период будет достаточно большой у последовательности, то это будет образующая.

Личные ключи скрываются от всех.

Двумя абонентами публикуетсяшифровка своего ключа: образующая q в степени и . При обмене ключами абоненты пересылают именно эту степень.

Вычисляется общий ключ: абонент посылает обратно шифровку

Ключ получается равным на обеих сторонах. Далее этот ключ используется, например в RSA.

Достоинства методов с открытыми ключами:

Редкая смена ключей.
Имеется 1 ключ на абонента.
Для подтверждения подлинности абонента можно связаться по телефону.

Общий недостаток методов с открытыми ключами: не позволяется проводить идентификацию партнера. Далее начинает работать как один из адресатов, собирает статистику. Метод Диффи и Хеллмана в 30 раз быстрее, чем RSA. В 5 раз быстрее по сравнению с Эль-гамалем. И по криптостойкости тоже самое.

Вычислительные алгоритмы для криптологии. Алгоритм Евклида.

Алгоритм для нахождения НОД 2х целых чисел, одновременно не равных 0.НОД(a, b) = gcd(a, b).

Если оба числа делятся на некий делитель, то и их разность делится на это число (из большего вычитают меньшее). Разность имеет тот же НОД, что и об исходных числа.

=> .

Разность двух чисел меньше большего числа, т.е. .

НОД можно получить:

Делить на все числа до половины меньшего из двух чисел.
Последовательно вычитая из большего числа меньшее до тех пор, пока остаток не будет меньше b. Делитель на каждом шаге будет сохраняться (т.е. число 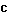). Этот способ предпочтительнее.

Многократное вычитание можно заменить делением. Получим НОД последовательным вычитаниемдо тех пор, пока остаток не будет меньше b. Дальше меняем местами b и остаток, продолжаем вычитания. Можем ускорить алгоритм: если у нас остаток – четное число, а вычитаемое – нечетное, то можно сделать сдвиг остатка на бит вправо.

Далее — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть