Пример обмена информацией по методу Эль-гамаля.

Пусть есть два абонента А и В. Абонент А желает передать абоненту В сообщение: число 37. В середине есть канал, который постоянно перехватывает. Канал не надежен. Перед передачей А и В договариваются о том, что выбирают некий ключ, который не говорят ни кому. Ключ выбирается из диапазона от 1 до 155.

1. А выбирает ключ K₁=133=85h. Открытый текст S₀= 37.

В выбирает ключ K₂=79=45h.

Если над сообщением дважды проделать операцию XOR, то получим исходное сообщение.

2. А составляет сообщение S₁=S₀xorK₁=160.

3. В получает число, шифрует его S₂=S₁xorK₂=EF, пересылает его обратно.

4. Абонент Ашифрует число S₃=S₂xorK₁=60h.

5. В принимает число, S₄=S₃xorK₂=25h=37.Получили расшифрованное сообщение.

У этого примера малая криптостойкость, каков бы ни был ключ.

Алгоритм обмена сообщениями по Эль-гамалю (модификация дифи).

Метод шифрования с открытым ключом.

1. Задается большое простое число , которое известно всем пользователям. Сообщения представляются целыми числами из интервала 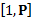и передаются последовательно.

- открытый ключ.

2. Пользователи A и B выбирают числа 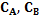взаимно простые с 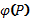(функцией Эйлера от ) и такие, что . Это гарантирует, что при возведении в степеньрезультат никогда не будет = 1, иначе расшифровка была бы невозможна. – закрытые ключи.

3. Пользователи A и B вычисляют инверсии своих закрытых ключей 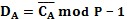и . ( )

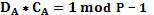4. Передача сообщений производится в два приема.

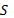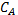   1. А имеет сообщение , шифрует его своим ключом – возводит в степень по модулю 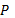, отправляет В сообщение .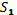

В получает , шифрует его своим ключом – возводит в степень по модулю и отправляет А сообщение .

2. А получает это число, снимает свой ключ – возводит сообщение в степень по модулю , отправляет Всообщение .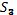

B, получив это число, возводит его в степень по модулю и в результате получает сообщение .

Доказательство: следует непосредственно из теоремы Эйлера.

( = = …

Недостаток: метод не позволяет производить идентификацию партнера.

Алгоритм rsa

Шифр RSA (Rivest, Shamir, Adleman)был предложен в 1978 г. и долгое время был принят за основу в стандартах США. Алгоритм:

1. Даны 2 очень больших простых числа и .

2. Вычисляется модуль – произведение этих чисел:

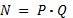
3. Вычислить функциюЭйлера .

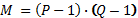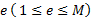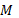4. Выбирается случайное целое число , взаимно простое с . gcd(e, M) = 1.

5. Вычислятся число 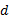, мультипликативно обратное к числу 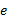по модулю .

Такое что .

6. Получаем, что пара –открытый ключRSA. Сообщается всем людям в сети.

Пара –закрытый ключRSA.

7. Шифрование сообщения. Если S – сообщение, то шифр .

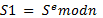8. Расшифрование. .

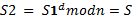ПримерRSA:

S = 2 (надо передать).

P = 5, Q = 7.

= 35.

=4 * 6 = 24

e = 11 – открытый ключ.

d* 11 = 1 mod 24. Если d = 11, то d*e = 121 = 24*5 + 1.

Шифруем:

Расшифровываем:

Доказательство:

R = (S^E)^D mod N = S^E*D mod N =S^M*K+1 mod N =S

S^MmodN =1

Ч.т.д.

Для ускорения вычислений лучше брать открытый и закрытый ключ небольшими, но М – результат их перемножения всего на несколько разрядов меньше N, то есть один из них будет небольшим, но это угрожает раскрытием шифра. Методы факторизации помогают вскрыть RSA.

Для ускорения обработки больших чисел разработаны спецпроцессоры RSA. Но все равно слабое место метода – малое быстродействие. Используется при передаче сеансовых ключей. Далее используется что-то другое, к примеру простая замена.

Несимметричный метод – шифруется и расшифровывается разными ключами. Это были алгоритмы передачи сообщений.

Разработчики избегают использовать числа N, меньше, чем в 200 десятичных разрядов.