Идеалы и классы вычетов.

Идеал – подмножество элементов кольца R, обладающее свойствами:

1. I – подгруппа аддитивной группы кольца R.

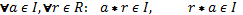2. . (Любой элемент кольца, умноженный на элемент идеала в результате дает элемент идеала).

Пример: в кольце положительных, отрицательных чисел и нуля множество всех чисел, кратных целому образует идеал. Но это еще и подгруппа аддитивной группы.

Классы вычетов.

Так как идеал по определению является подгруппой, по нему можно образовать смежные классы. И в этом случае смежные классы называют классами вычетов.

Идеал:

0 =
=
=

Идеал образует первую строчку разложения.

Каждая следующая строка – сложение образующих элементов с элементами идеала.

– последовательно выбираемые элементы.

По своим свойствам идеал наследует все свойства смежных классов.

По аналогии с последним примером можно определить операции сложения и умножения для вычетов:

Сложение: . Сложение двух множеств с образующими и является множетсвом с образующим (это элемент).

Умножение: .

Следствие:

Теорема: классы вычетов по идеалу в некотором кольце образуют кольцо и это кольцо называют кольцом классов вычетов.

Эквивалент: Т.е. если образующие элементов образуют кольцо, то и классы вычетов образуют кольцо.

Пример: идеал, образованный всеми четными числами. Получим 2 класса вычетов: {0} и {1}.

Здесь кольцо вычетов определяет арифметику (сложение и умножение) по модулю 2.

Идеалы и классы вычетов целых чисел.

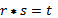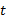1. Если r,s,t – целые числа и , то говорят, что делится на 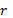или – делитель ( ).

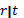2. Если целое 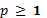делится только на p и 1, то число p – простое.

3. Для любой пары чисел s и d существует единственная пара чисел q и r такая, что:

. т.е. любое число можно разделить на другое с остатком.

Этаформула отражает алгоритм деления Евклида.

Следствия из алгоритма деления Евклида:

1. НОД чисел r и sможно представить в виде 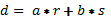, где a и b – целые числа.

2. Любое целое число можно представить в виде произведения степеней простых чисел.

Теорема: Совокупность целых чисел образует идеал тогда и только тогда, когда все они кратны некоторому целому числу.

Следствие теоремы: кольцо классов вычетов по идеалу m называется кольцом целых чисел по модулю m. J={m}.

Теорема 2: Каждый класс вычетов по модулю m содержит либо «0», либо целое положительное число <m. «0» принадлежит идеалу, остальные числа, меньшие m – различным классам вычетов.

Т.о.получаем 1 идеал и (m-1) смежных классов.

Обычно вычеты – это числа от 0 до (m-1). Это так называемые малые числа.

Итоговая теорема:

Кольцо классов вычетов по модулю m является полем тогда и только тогда, когда m – простое число. Такие поля – простые поля или поля Галуа из p элементов и записываются как:

GF(p) GaluaField.

У модульных операций нет переноса, поэтому можно делать машины простые и быстрые. Именно поэтому изначально была идея создания первых машин на основе арифметики остатков.

Пример относительно вычетов:

Возьмем класс вычетов по модулю m=6. Для этих классов можно спокойно выполнять сложение и умножению по модулю.R = {0, 1, 2, 3, 4, 5}.

0	6	-6	12	-12	…
1	7	-5	13	-11	…
2	8	-4	14	-10	…
3	9	-3	15	-9	…
4	10	-2	16	-8	…
5	11	-1	17	-7	…

Теорема: кольцо, образованное совокупностью остатков от деления на простое число m, является полем.

Докакательство: пусть m – непростое число, тогда имеет место: , где r и s – некратные mчисла: . В терминах остатков: .

Если это поле, то каждый элемент обладает обратным – R.

Тогда по ассоциативному закону.

Получаем противоречие, т.к. изначально предположили, что r и s . Тогда ни r, ни s не имеют обратных элементов, а если обратных элементов нет, то такое кольцо не является полем.

Докажем, что если m– простое, то для каждого элемента кроме 0 существует обратный ему элемент. Словесное рассуждение: каждое кольцо чисел, образованное остатками от деления на m, содержит по крайней мере 1 число и s<m. Поскольку единица совпадает со своим обратным элементом, то можно считать, что s> 1. Тогда НОД(s,m)=1.

По следствию из алгоритма Евклида: . Возьмем от обеих частей остатки от деления на m: .

Но a – остаток от деления на m. . Получаем, что – число, обратное .

Пример: рассмотрим обратные элементы для поля, образованного остатками от деления на 7. Все ненулевые элементы имеют обратные:

	1	2	3	4	5	6
обратный элемент	1	4	5	2	3	6

Пример классов вычетов над конечным кольцом – это остатки от деления по модулю 15:

идеал – числа, кратные 3:	0	3	6	9	12
Смежные классы	1	4	7	10	13
	2	5	8	11	14

Для любых элементов из первой строчки – их произведение с любыми другими принадлежит идеалу. Например, 3*7 = 21. Возьмем модуль 15: 21 mod 15 = 6, а 6 принадлежит идеалу.

Пример:N - Остатки от деления на 15:

N	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
N mod 3	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2
Nmod 5	0	1	2	3	4	0	1	2	3	4	0	1	2	3	4

Посмотрим на эти числа сверху. Нарисуем прямоугольник. Координатами являются кольца: X – Остатки от деления на 3, Y – Остатки от деления на 5.

… 2 5 11 2 8 14 1 10 1 7 13 4 0 0 6 12 3 9 X/Y 0 1 2 3 4 …

Таблица с выровненными по координатам числам:

10	13	1	4	7	Остаток от деления на 3 = 1
5	8	11	14	2	Остаток от деления на 3 = 2
0	3	6	9	12	Идеал 3
Идеал 5	Остаток = 1	Остаток = 3	Остаток = 4	Остаток = 2

2 идеала в виде осей координат. По идеалам расположены числа, кратные 3 и 5.

Дело в том, что 15 – непростое число. 3 и 5 – делители этого числа. В каждом из смежных классов остатки деления на 3 и на 5 – это постоянная величина. 5, 8, 11, 14, 2 – все остатки деления на 3 = 2.А в верхнем ряду остатки равны 1.

Если взять множество мощности 105 = 3*5*7, то получим уже 3 сомножителя в определении мощности группы, поэтому можно построить 3 идеала для чисел, кратных этим сомножителям. Если выделить идеалы для этих чисел, то сможем построить уже трехмерную фигуру.

Многомерную фигуру можно построить для любого числа элементов множетсва.

Число называется первоначальным или простым, если оно не есть сумма равных слагаемых, больших 1. Поэтому ряд простых чисел можно легко составить, используя решето Эратосфена.

1 – не принадлежит ни к простым, ни к составным числам по определению.

2 – простое. Вычеркиваем все числа, которые можно получить суммированием этого числа – 4, 6, 8, 10, 12 …

Дальше вычеркиваем числа, которые можно получить суммированием тройки и т.д. Остаются только простые числа.

Для поиска простых чисел требуется итераций.

Составное число – сумма равных слагаемых, больших 1.