Подгруппыи смежные классы.

Подгруппа H – некоторое подмножество элементов группыG, если оно удовлетворяет всем аксиомам группыG. Для того, чтобы определить, является ли H подгруппой, необходимо проверить:

Замкнутость: , то произведение .

Наличие обратного элемента: если , то обратный элемент .

Остальные аксиомы выполняются автоматически: если множество H замкнуто относительно групповой операции и содержит обратные элементы, то оно должно так же содержать единичный элемент группы и для группы должен выполняться ассоциативный закон.

Пример подгрупп:

В группе всех целых чисел, совокупность чисел, кратных m является подгруппой для любогоm. Для m = 1 в виде подгруппы получим ту же самую группу (сама группа G является своей подгруппой).

Элементы группы G:

Элементы подгруппыH:

Рассмотрим таблицу. 1ая строка состоит из элементов подгруппы, причем начинается с единичного элемента и каждый элемент подгруппы появляется в строке только 1 раз. Первым элементом второй строки может быть любой элемент группы, не входящий в первую строку,а все остальные элементы строки получаются умножением слева на первый элемент строки всех элементов подгруппы. Так же образуются все остальные строки. Каждая с неиспользованным прежде элементом в начале строки до тех пор пока каждый элемент группы не войдет в таблицу.

			…
			…
…	…	…	…	…
			…

Совокупность элементов в строке таблицы называется левым смежным классом, а элемент, стоящий в первом столбце строки, называется образующим смежного класса.

Правые смежные классы могут быть построены аналогичным образом. Разделение имеет смысл только для некоммутативных групп. Таблица задает разложение группы на смежные классы.

Теорема: 2 элемента и входят в один и тот же левый смежный класс по подгруппе H в тогда и только тогда, когда произведение , т.е. их частое .

Замечание: теорема записана в мультипликативной форме. Для аддитивных групп теорема выглядит так:

Когда сумма , т.е. когда их разность принадлежит подгруппе.

Это видно из самого построения таблицы.

Теорема: каждый элемент группы G принадлежит одному и только одному смежному классу элементов по подгруппеH.

Порядок группы – количество элементов в группе (мощность множетсва).

Число различных смежных классов в разложении группы G по подгруппе H – это индекс H в G.

Построение смежных классов по шагам:

1. Взяли подгруппу H из 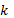элементов. Записали их в одну строчку. элементов можно найти.

2. Взяли 1 из элементов группы не принадлежит подгруппе => получили смежный класс из еще k элементов.

3. Если при этом в группе не осталось ни 1 элемента, который не входит ни в подгруппу, ни в смежный класс, то процесс закончен. Иначе строим еще подгруппу, каждый раз выбираяkновых элементов.

n) На последнем шаге мы заберем из группы последние k элементов и внесем их. Оставшихся элементов не может быть меньше k, т.к. мы всегда получаем только всю строку

Теорема лагранжа:

(порядок H) * (индекс H в G)=(порядок группыG).

Следствие: порядок любой подгруппы является делителем порядка группы. Количество элементов подгруппы кратно количеству элементов группы.

Следствие из теоремы Лагранжа: порядок подгруппы меньше порядка группы по крайней мере в 2 раза. Т.о. в группе строчек минимум 2. если их больше, то порядок подгруппы еще меньше.

Пример: если есть аддитивная группа G, состоящая из положительных целых чисел и нуля, то можно выделить подгруппу H, содержащую числа, кратные какому-либо числу.

Все малые числа от 0 до (n-1) принадлежат различным смежным классам. Необоходимо, чтобы элемент (–a+b) принадлежал подгруппе и был кратен этому числу n. Т.к. малые числа принадлежат разным подгруппам, то их удобно взять за образующие для смежных классов.Смежных классов с другими образующими не существует. В данном случае представлены бесконечные группы, но утверждение распространяется и на них

Пример:

n=3, строим смежные классы:

0	3	-3	6	-6	9	-9	…	{0} = H
1	4	-2	7	-5	10	8	…	{1}
2	5	-1	8	-4	11	-7	…	{2}

{0}, {1}, {2] – это изображение смежных классов.

Группа коммутативна, поэтому можно определить операцию сложения для смежных классов. При суммировании классов {1} и {2} получим элементы смежного класса {0}.

Таблица суммирования смежных классов (таблица сложения чисел по mod 2):

+	{0}	{1}	{2}
{0}	{0}	{1}	{2}
{1}	{1}	{2}	{0}
{2}	{2}	{0}	{1}