Регистр с обратной связью.

Регистр сдвига с линейной обратной связью состоит из двух частей: регистра сдвига и функции обратной связи. Функция обратной связи представляет собой сумму по модулю 2 (xor) некоторых битов регистра, называемых отводами.

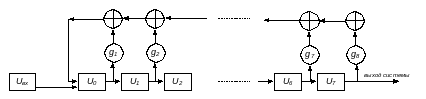
всегда.

Если на вход ничего не подавать, то получим генератор псевдослучайных чисел. Будем получать случайную последовательность на выходе по тактам:

Аналогично можем найти U1 и U0.

Смысл – элементы такой последовательности зависимы. Если известны n тактов гаммы, то её можно восстановить полностью.

Пусть теперь есть только 1 единица в рабочем регистре, то получаем некую стандартную последовательсноть. В регистр сразу проваливается магический полином, гамму, полученную из одной 1 модем считать базовой. Помещая 1 в разные ячейки рабочего регистра, получим последовательность, сдвинутую на разное число тактов. Из n базовых последовательностейможно составить любую последовательность. Если в регистр поместим любое число единиц и нулей расположенных произвольно, то каждая даст свою последовательность. Суммируя их по модулю 2 получим то же, что было бы при регистре, подностью заполненном 1ми. Свойство линейности.

Шифрование при помощи случайной последовательности (гамма-последовательности).

1. Генераторы случайных последовательностей позволяют получить гамма-последовательность. Если магический полином неприводим, примитивен степени n, то длина гамма последовательности равна .

2. Последовательность максимального периода имеет равномерный спектр.

Доказательство:основано на том, что функция автокорреляции этой последовательности – дельта-функция. Её спектр равномерен, она походит на случайный белый шум.

3. Если есть текст с неравными вероятностями нулей и единиц.

Вероятность появления «1»в тексте: .

Вероятность появления «0»в тексте: .

Для вероятности .

«1»на выходе, если возникает комбинация в тексте и в гамме «0 xor1» или «1xor0»

Вероятность появления «1» в зашифрованном тексте:

Независимо от текста получаем, что вероятности появления нулей и единиц будут равны (хотя в открытом они разные).

Гамма последовательность зависит от начальной загрузки регистра, поэтому можно использовать ключ.

Потоковые шифры.

Гамма-последовательности использовались в большинстве потоковых шифров. Генераторы гамма-последовательности простые (особенно в аппаратном исполнении).

Недостаток – сложность и малоэффективность в программном исполнении, малая криптостойкость.

Более стойкий генератор можно сделать, взяв более длинный регистр или чаще меняя пароли.

Нелинейные функции: можно взять несколько регистров разной длины.

Фильтрующий генератор – 1 регистр с обратной связью, из гамма-последовательности составляем нелинейную функцию.

Для разных регистров используются разные частоты.

Генераторы:

1. с прямой связью – выход нодго генератора управляет тактовой частотой другого.

2. с обратной связью – выход одного из регистров генератора управляет тактовой частотой этого же генератора.

Рассмотрим некоторые генераторы.

Генератор Греффе.

Используется n регистров сдвига с линейной обратной связью (РСЛОС).

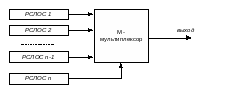
РСЛОСn управляет мультиплексором – используется для выбора из регистров.

Период такого генератора равен НОК отдельных генераторов (общий период равен их произведению, а линейная сложность – двоичный логарифм из этого произведения – она не превосходит общей длины всех регистров). Если периоды кратные один другому, то линейная сложность уменьшится.

Криптографически этот генератор слаб.Он подвержен корреляционным атакам. Информация о состояниях генераторов РСЛОС 1, …, РСЛОС n-1 содержится в его выходной последовательности.Эта последовательность легко вскрывается.