Генераторы случайных последовательностей.

Псевдослучайные последовательности.

Работа схемы шифрования:

Ключ+алгоритм = генератор гаммы . Генератор гаммы выдает ключевой поток (гамму). Биты шифротекста получаются с помощью применения операции XOR битов открытого текста и битов гаммы.Расшифрованиесообщения производится операцией XOR между той же самой гаммой и зашифрованным текстом: .

Желательно, чтобы последовательность была случайна: если последовательность битов гаммы не имеет периода и выбирается случайно, то взломать шифр невозможно. Но генерируются псевдослучайные последовательности, каждая из которых периодична. Обычно применяют ключ меньшей длины (например, 128 бит). С помощью него генерируется псевдослучайная гаммирующая последовательность (она должна удовлетворять постулатам Голомба).

Определения:

1. Последовательность ( 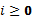) называется периодической с периодом p, если p-наименьшее положительное чилое, для которого .

2. Пакет длины k есть подпоследовательность , содержащая k идентичных символов, ограниченных символами другого вида. При этом иногда различают два вида пакетов: блок, состоящий из k единиц и пропуск- пакет, состоящий из 100 нулей.

3. Предположим, есть две копии одной и той же последовательности периода p, сдвинутые относительно друг друга на некоторое значение k. Тогда для каждого k, 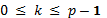, мы можем подсчитать количество согласованностей между этими двумя последовательностями А(K), и количество несогласованностей D(k).

АвтокорреляцияAC(k)для каждого kв периодической последовательности с периодомpопределяется соотношением:

.

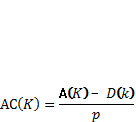А(K)- количество совпадений, D(k)- количество антисовпадений на отрезке длиной в 1 период последовательности.

Количество совпадений и антисовпадений в сумме = длина периода: .

.

{Si}при i>=0,{S_i+k}- последовательность Si, сдвинутая влево на k тактов.

Эта функция автокорреляции принимает различные значения по мере того, как d проходит все допустимые значения.

Пример:

Si= {11010000}, p=8

AC(k)={1,0,0,0,1/2,0,0,0}

Если k кратно p, то у нас А(k)=p, D(k)=0, тогда автокорреляция равна нулюи это фазовая корреляция.

Если к не делится на р, то говорят о противофазной корреляции.

Постулаты случайности последовательностей Голомба.

Постулаты для псевдослучайных двоичных последовательностей. Согласно им последовательность должна удовлетворять определенным ограничениям на встречаемость знаков, мулътиграмм и функцию автокорреляционную последовательности. Последовательности, удовлетворяющие постулатам, называют псевдошумовыми.

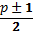1. Постулат G1.Количество нулей и единиц на протяжении периода равны насколько это возможно, то есть оба равны для четного р и для нечетногоp.

Т.е. единицы и нули последовательности возникают с почти равной вероятностью. Количество единиц в каждом периоде должно отличаться от количества нулей не более, чем на единицу.

2. Постулат G2. В каждом периоде половина пакетов (из одинаковых символов) должна иметь длину один, одна четверть должна иметь длину два, одна восьмая должна иметь длину три и т.д. Более того, для каждой из этих длин должно быть одинаковое количество серий из "1" и "0".

После символов {011}символ «0», приводящий к образованию блока длины 2,имеет туже вероятность, что символ появление символа «1». Предполагаем независимость каждого предыдущего символа.

Постулат утверждает, что определенные мульти­граммы возникают с соответствующей им вероятностью. Мультиграмма (m-грамма) — набор из m знаков алфавита.

3. Постулат G3. Для любой последовательностиавтокорреляционная функция (АКФ) должна принимать лишь два значения.Противофазная автокорреляция AC(k) имеет одно и тоже значение для всех k.

Пример:

S = 0 1 1 0 0 1 0 0 0 1 1 1 1 0 1. Проверим выполнение постулатов:

1. Количество «0» = 7, количетсво «1» = 8.

2. В периоде 8 пакетов. 4 пакета имеют длину 1, 2 пакета – длину 2 («11», «00»), 1 пакет имеет длину 3 («000»), 1 пакет имеет длину 4 («1111»).

3. Если последовательность не сдвигать, то AC(0)=0, а если сдвигать на любое количество разрядов, то будет получать одинаковое значение .

Свойства:

1. Период последовательности должен быть очень большим для удачного кодирования. Елси он короче текста, то будет повторяться и с использованием статистики можно будет вскрыть код.

2. Последовательность нужно легко генерировать и воспроизводить.

3. Знание части открытого текста вместе с соответствующим закрытым не должно позволять производить расшифровку полностью.