АлгоритмCrc:

Работает над битовым полем. При этом битовый поток рассматривают как полином с коэффициентами из поля , то есть 0 и 1.

Определяющим является полином с коэффициентом, называемый так же магическим.

1. Исходный поток битов умножают на 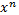.Это эквивалентно сдвигу влево и приписыванию справа n нулей.

2. Полином делят на и запоминают остаток :

.

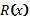3. Получают результат T(x), суммируя с остатком :

.

4. Посылают результат абоненту(сдвинули и приписали остаток в хвост).

5. Пользователь, получив , делит его на . При правильнойпередаче делится на без остатка. Противный результат свидетельсвует об ошибках.

Наиболее популярные магические полиномы:

. для этого полинома сравнительно мало единиц.

.

.

.

CRC-Ethernet = 0x104611db7.

CRC-zip=0xdebb20e3.

В архиваторе: В регистр чаще всего загружается начальное значение всеми единицами, после деления полученный crc посткондиционирует = вместо полученной величины crc кода используют его двоичное дополнение. Для чего: в архиваторе не использовалась начальная загрузка. Там были все нули. Это приводило к тому, что если в нашем файле в самом началае стоят нули, то регистровая схема не будет работать пока не придет первая единица. То есть файлы с разным числом нулей на входе не будут отличаться друг от друга. Вообще-то для текстовых файлов начальные элементы равные нулю запрещены. Но для других файлов такие случаи могут быть. Значит лучше использовать инициализацию всеми единицами.

Выбор полинома.

При конкретной задаче полином имеем право выбрать.

Передаваемое сообщение – произведение двух полиномов: выбранного и магического. Последние несколько битов– остаток отделения выбранного на магический. Прибавление к концу полинома остатка от деления, дополняем наш полином до кратного магическому полиному.

Если сообщений было повреждено, то было сообщение в виде T(x)+E(x), E(x) – вектор ошибки. Единицы там, где ошибки. T(x) – истинное значение.

Когда делим полученое на магический полином, то получаем в качестве остатка Е(х) по модулю магического полинома.

Если получили такой остаток, то если Е(х) принадлежит идеалу, то ошибка будет равна нулю. Наша задача при выборе полинома заключается в том, чтобы найти полином, произведение которого на произвольный полином будет отличаться от заданного вида ошибок.

Типы ошибок:

1. Однобитовые ошибки. Е(х)=10…0. На вход системы подаем E.Такая ошибка может всегда быть обнаружена при условии, что в полиноме Р(х) есть минимум две единицы, так как любое произведение полинома Р(х) на другой есть сложение по модулю, то нельзя получить единичную единицу сдвинутую относительно начала. То есть в результате будет хотя бы 2 единичных бита. Так как сдвиг полинома- умножение на х. единица остается.

2. Двухбитовые ошибки:

Е(х)=10…010…0.

Такие ошибки можно обнаруживать. Нужно выбрать такой P(x), который не содержит многочленом вида 11, 101, 1001, 10001, ….

Такие полиномы, например x^15+x^14+x^1 – единичные биты, которые не могут быть делителями представленного. То есть будет обнаруживать двухбитовые ошибки.

3. Ошибки с нечетным количеством битов. Можно определить любое нечетное число ошибок, если выбрать полином Р(х) с четным количеством единиц.

Умножение в CRC – это операция XOR для постоянного значения регистра, но с разными смещениями.

XOR – операция переключения битов.

Большинство CRC-полиномов содержит четное количество единиц.

4. Пакетные ошибки.

Типовое представление: Е=000…011111…11100…0. Есть несколько нулей в середине.

Для выявления таких ошибок младший бит магического полинома рекомендуется установить в 1. Тогда до тех пор пока полином Р(х) шире,чем последовательность единиц пакета, пакетные ошибки будут выявляться.

Для пакетных ошибок вероятность равна , где n- ширина пакета.

Если ошибки возникают неслучайно, то

Вообще можно построить текст так, что CRC не заметит замену.

Для усиления устойчивости CRC: в рабочие регистры в начальном такте можно записать какое-то начальное значение. Это хорошо еще когда файл в начале состоит из нулей.